UVA1205 Color a Tree 题解
Post time: 2020-08-05 21:23:50
题目大意大家可以打开题目描述中PDF看，下面开始讲题解。
一、思维尝试：
首先我们思考，为了让总的结果最小，整个树中权值最大的点一定在他的父亲节点染色之后马上染色。所以我们首先考虑将这两个点合并，继续在整个图中找最大权值……最后只剩根节点的时候合并结束，输出结果即可。
这个思路看起来不错，但是有一个问题：这个“最大权值”指的是什么呢？如果仅仅指每一个点的初始染色代价，那么只要构造一个像这样的图：（节点上的值表示每个点染色代价）
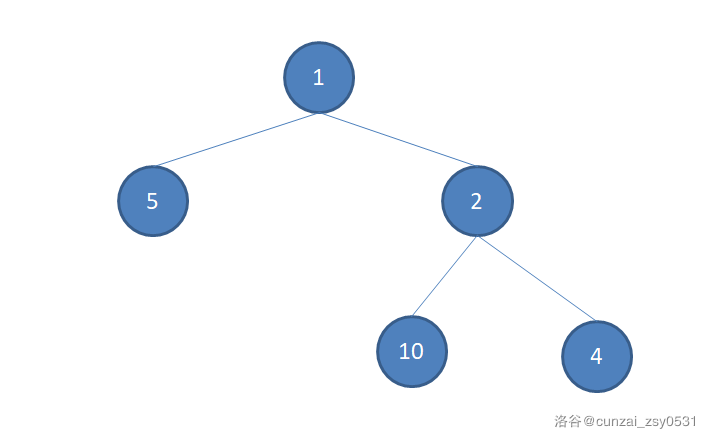
（插一句：这个数据是我们机房巨佬 @sdfz171047 造出来的，真的好巧(du)妙(liu)）
你会发现我们合并顺序是这样的：
10->2
5->1
4->2
2->1
这样的话，相当于的染色顺序为：
1->5->2->10->4
它的代价为：
1*1+5*2+2*3+10*4+4*5=77
然而，如果你用下面这个顺序染色：
1->2->10->5->4
代价就是：
1*1+2*2+3*10+5*4+4*5=75
这样证明了以节点初始染色代价为贪心策略是不正确的。
二、如何推贪心？
我们想要知道贪心策略，必须要找到对于图中任意三个点的正确顺序。我们设这三个点为 \(x,y,z\)，并且假定 \(x,y\) 已经捆绑了，必须先染 \(x\) 再染 \(y\)。那么会有两种情况：
- \(x\to y\to z\) 代价是 \(x+2y+3z\)
- \(z\to x\to y\) 代价是 \(2x+3y+z\)
比较两式可用作差法，相减可得 \(2z-(x+y)\)，除以 \(2\) 得 \(z-\frac{x+y}{2}\)
这样我们就找到了贪心的权值，我们可以称它为一个点的“等效权值”，我们用 \(cnt_i\) 表示以 \(i\) 为根的子树大小，\(sum_i\) 表示以 \(i\) 为根的子树染色代价之和，那么每个点的等效权值 \(W_i\) 为：
所以我们维护一个大根堆，每次取出当前最大的 \(W_i\)，将这个点与 \(fa_i\) 合并。
三、代码怎么实现？
我的做法是维护每个点后面染哪个点 \(nxt_i\)，最后从根节点开始通过这个 \(nxt\) 遍历整个树完成答案统计。
在结构体里，对于每个点存这样几个数据：
a[i].fa //父亲节点编号
a[i].val //初始染色代价
a[i].last //以i为根合并之后的最后一个染色点编号
a[i].nxt //在i号点后面染色的点
a[i].vis //i有没有向上合并过
考虑将 \(u\) 合并到 \(f\)（注意顺序）：
- 如果 \(f\) 已经向上合并过，那么就继续往上找，即
f=a[f].fa - \(u\) 应该在 \(f\) 的最后一个点后染色，即
a[a[f].last].nxt=u - \(f\) 的最后一个点改为 \(u\) 的最后一个点，即
a[f].last=a[u].last - 更新 \(W_f\)，将 \(f\) 入队。把 \(u\) 的
vis设为 \(1\)，表示已经合并完了。
最后扫一遍即可得到结果。
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int N=1000+13;
struct Node{int val,fa,last,pos,nxt,cnt,sum;}a[N];
struct Queue{
int v;double w;
bool operator <(const Queue &a)const{return w<a.w;}
};
priority_queue<Queue>q;
int n,root,ans;
bool vis[N];
inline void clear(){
ans=0;
memset(a,0,sizeof(a));
memset(vis,0,sizeof(vis));
while(!q.empty()) q.pop();
}
int main(){
while(scanf("%d%d",&n,&root)==2&&(n||root)){
clear();
for(int i=1;i<=n;++i){
scanf("%d",&a[i].val);
a[i].last=a[i].pos=i;
a[i].sum=a[i].val,a[i].cnt=1;
if(i!=root) q.push((Queue){i,a[i].val*1.0});
}
for(int i=1,u,v;i<n;++i) scanf("%d%d",&u,&v),a[v].fa=u;
while(!q.empty()){
int v=q.top().v,u=a[v].fa;q.pop();
if(vis[v]) continue;vis[v]=1;
while(vis[u]&&u!=root) u=a[u].fa;
a[a[u].last].nxt=v,a[u].last=a[v].last;
a[u].cnt+=a[v].cnt,a[u].sum+=a[v].sum;
double w=a[u].sum*1.0/a[u].cnt;
if(u!=root) q.push((Queue){u,w});
}
for(int i=1,u=root;i<=n;++i,u=a[u].nxt) ans+=i*a[u].val;
printf("%d\n",ans);
}
return 0;
}
