POJ - 1149 PIGS (建图思维+最大流)
题目分析
(以下均为 Edelweiss 大佬的思路,博主承认自己写不了这么好,但是学习的心促使我记录下这个好题的写法,所以代码是我写的)
【题目大意】 有 M 个猪圈,每个猪圈里初始时有若干头猪。一开始所有猪圈都是关闭的。依 次来了 N 个顾客,每个顾客分别会打开指定的几个猪圈,从中买若干头猪。每 个顾客分别都有他能够买的数量的上限。每个顾客走后,他打开的那些猪圈中的 猪,都可以被任意地调换到其它开着的猪圈里,然后所有猪圈重新关上。问总共 最多能卖出多少头猪。(1 <= N <= 100, 1 <= M <= 1000)
举个例子来说。有 3 个猪圈,初始时分别有 3、1 和 10 头猪。依次来了 3 个顾客, 第一个打开 1 号和 2 号猪圈,最多买 2 头;第二个打开 1 号和 3 号猪圈,最多买 3 头;第三个打开 2 号猪圈,最多买 6 头。那么,最好的可能性之一就是第一个 顾客从 1 号圈买 2 头,然后把 1 号圈剩下的 1 头放到 2 号圈;第二个顾客从 3 号圈买 3 头;第三个顾客从 2 号圈买 2 头。总共卖出 2+3+2=7 头。
【建模方法】 不难想象,这个问题的网络模型可以很直观地构造出来。就拿上面的例子来说, 可以构造出图 1 所示的模型(图中凡是没有标数字的边,容量都是∞):
- 三个顾客,就有三轮交易,每一轮分别都有 3 个猪圈和 1 个顾客的结点。
- 从源点到第一轮的各个猪圈各有一条边,容量就是各个猪圈里的猪的初始 数量。
- 从各个顾客到汇点各有一条边,容量就是各个顾客能买的数量上限。
- 在某一轮中,从该顾客打开的所有猪圈都有一条边连向该顾客,容量都是 ∞。
- 最后一轮除外,从每一轮的 i 号猪圈都有一条边连向下一轮的 i 号猪圈, 容量都是∞,表示这一轮剩下的猪可以留到下一轮。
- 最后一轮除外,从每一轮被打开的所有猪圈,到下一轮的同样这些猪圈, 两两之间都要连一条边,表示它们之间可以任意流通。

这个网络模型的最大流量就是最多能卖出的数量。图中最多有 2+N+M×N≈100,000 个结点。这个模型虽然很直观,但是结点数太多了,计算速 度肯定会很慢。其实不用再想别的算法,就让我们继续上面的例子,用合并的方 法来简化这个网络模型。
首先,最后一轮中没有打开的猪圈就可以从图中删掉了,也就是图 2 中红色 的部分,显然它们对整个网络的流量没有任何影响。
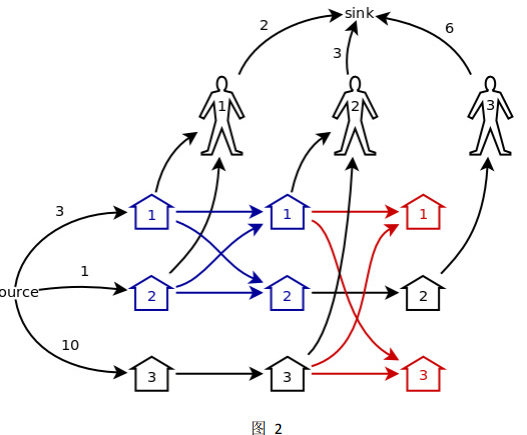
接着,看图 2 中蓝色的部分。根据我总结出的以下几个规律,可以把这 4 个 点合并成一个:
规律 1. 如果几个结点的流量的来源完全相同,则可以把它们合并成一个。
规律 2. 如果几个结点的流量的去向完全相同,则可以把它们合并成一个。
规律 3. 如果从点 u 到点 v 有一条容量为∞的边,并且点 v 除了点 u 以外没 有别的流量来源,则可以把这两个结点合并成一个。
根据规律 1,可以把蓝色部分右边的 1、2 号结点合并成一个;根据规律 2, 可以把蓝色部分左边的 1、2 号结点合并成一个;最后,根据规律 3,可以把蓝 色部分的左边和右边(已经分别合并成了一个结点)合并成一个结点。于是,图 2 被简化成了图 3 的样子。也就是说,最后一轮除外,每一轮被打开的猪圈和下 一轮的同样这些猪圈都可以被合并成一个点。
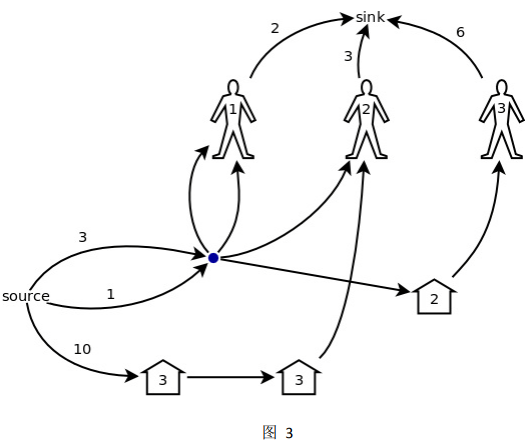
接着,根据规律 3,图 3 中的蓝色结点、2 号猪圈和 1 号顾客这三点可以合 并成一个;图 3 中的两个 3 号猪圈和 2 号顾客也可以合并成一个点。当然,如果 两点之间有多条同向的边,则这些边可以合并成一条,容量相加,这个道理很简 单,就不用我多说了。最终,上例中的网络模型被简化成了图 4 的样子。

让我们从上图 中重新总结一下构造这个网络模型的规则:
- 每个顾客分别用一个结点来表示。
- 对于每个猪圈的第一个顾客,从源点向他连一条边,容量就是该猪圈里的 猪的初始数量。如果从源点到一名顾客有多条边,则可以把它们合并成一 条,容量相加。
- 对于每个猪圈,假设有 n 个顾客打开过它,则对所有整数 i∈[1, n),从该 猪圈的第 i 个顾客向第 i + 1 个顾客连一条边,容量为∞。
- 从各个顾客到汇点各有一条边,容量是各个顾客能买的数量上限
拿我们前面一直在讲的例子来说:1 号猪圈的第一个顾客是 1 号顾客,所以 从源点到 1 号顾客有一条容量为 3 的边;1 号猪圈的第二个顾客是 2 号顾客,因 此从 1 号顾客到 2 号顾客有一条容量为∞的边;2 号猪圈的第一个顾客也是 1 号 顾客,所以从源点到 1 号顾客有一条容量为 1 的边,和之前已有的一条边合并起 来,容量变成 4;2 号猪圈的第二个顾客是 3 号顾客,因此从 1 号顾客到 3 号顾 客有一条容量为∞的边;3 号猪圈的第一个顾客是 2 号顾客,所以从源点到 2 号 顾客有一条容量为 10 的边。
新的网络模型中最多只有 2 + N = 102 个结点,计算速度就可以相当快了。可 以这样理解这个新的网络模型:对于某一个顾客,如果他打开了猪圈 h,则在他 走后,他打开的所有猪圈里剩下的猪都有可能被换到 h 中,因而这些猪都有可能 被 h 的下一个顾客买走。所以对于一个顾客打开的所有猪圈,从该顾客到各猪圈 的下一个顾客,都要连一条容量为∞的边。
在面对网络流问题时,如果一时想不出很好的构图方法,不如先构造一个最 直观,或者说最“硬来”的模型,然后再用合并结点和边的方法来简化这个模 型。经过简化以后,好的构图思路自然就会涌现出来了。这是解决网络流问题 的一个好方法。
代码区

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<queue> #include<string> #include<fstream> #include<vector> #include<stack> #include <map> #include <iomanip> #define bug cout << "**********" << endl #define show(x,y) cout<<"["<<x<<","<<y<<"] " //#define LOCAL = 1; using namespace std; typedef long long ll; const int inf = 0x3f3f3f3f; const ll mod = 1e6 + 3; const int Max = 1e5 + 10; struct Edge { int to, next; int flow; }edge[Max]; int n, m, s, t; int val[Max]; //每个猪舍的猪的个数 int last[Max]; //记录上一个打开这个猪舍的人 int head[Max], tot; int dis[Max]; void init() { memset(head, -1, sizeof(head));tot = 0; memset(last, -1, sizeof(last)); s = 0;t = n + 1; } void add(int u, int v, int flow) { edge[tot].to = v; edge[tot].flow = flow; edge[tot].next = head[u]; head[u] = tot++; } bool bfs() //判断连通性,将图分层次 { queue<int>q; memset(dis, -1, sizeof(dis)); dis[s] = 0; q.push(s); //源点 while (!q.empty()) { int u = q.front();q.pop(); for (int i = head[u]; i != -1; i = edge[i].next) { int v = edge[i].to; if (dis[v] == -1 && edge[i].flow > 0) { dis[v] = dis[u] + 1; q.push(v); if (v == t) return true; } } } return false; } int dfs(int u, int flow_in) { if (u == t) return flow_in; int flow_out = 0; //实际流出流量 for (int i = head[u];i != -1;i = edge[i].next) { int v = edge[i].to; if (dis[v] == dis[u] + 1 && edge[i].flow > 0) { int flow_part = dfs(v, min(flow_in, edge[i].flow)); if (flow_part == 0)continue; //无法形成增广路 flow_in -= flow_part; flow_out += flow_part; edge[i].flow -= flow_part; edge[i ^ 1].flow += flow_part; if (flow_in == 0)break; } } return flow_out; } int max_flow() { int sum = 0; while (bfs()) { sum += dfs(s, inf); } return sum; } int main() { #ifdef LOCAL //freopen("input.txt", "r", stdin); //freopen("output.txt", "w", stdout); #endif while (scanf("%d%d", &m, &n) != EOF) { init(); for (int i = 1;i <= m;i++) scanf("%d", val + i); for (int i = 1, num, need;i <= n;i++) { scanf("%d", &num); int ans = 0; //记录从源点到这一结点的总流量 for (int j = 1, x;j <= num;j++) { scanf("%d", &x); if (last[x] == -1) { ans += val[x]; //这个猪圈的第一个顾客 } else //已经出现了,由前一次出现的位置向后建边 { add(last[x], i, inf);add(i, last[x], 0); } last[x] = i; } scanf("%d", &need); add(s, i, ans);add(i, s, 0); add(i, t, need);add(t, i, 0); } printf("%d\n", max_flow()); } return 0; }


