『ACM C++』 PTA 天梯赛练习集L1 | 001-006
应师兄要求,在打三月底天梯赛之前要把PTA上面的练习集刷完,所以后面的时间就献给PTA啦~ 后面每天刷的题都会把答案代码贡献出来,如果有好的思路想法也会分享一下~ 欢迎大佬提供更好的高效率算法鸭~
------------------------------------------------L1-001----------------------------------------------------------
这道超级简单的题目没有任何输入。
你只需要在一行中输出著名短句“Hello World!”就可以了。
------------------------------------------------L1-001----------------------------------------------------------
注解:水题
#include<stdio.h> int main() { printf("Hello World!"); return 0; }
------------------------------------------------L1-002----------------------------------------------------------
本题要求你写个程序把给定的符号打印成沙漏的形状。例如给定17个“*”,要求按下列格式打印
*****
***
*
***
*****
所谓“沙漏形状”,是指每行输出奇数个符号;各行符号中心对齐;相邻两行符号数差2;符号数先从大到小顺序递减到1,再从小到大顺序递增;首尾符号数相等。
给定任意N个符号,不一定能正好组成一个沙漏。要求打印出的沙漏能用掉尽可能多的符号。
------------------------------------------------L1-002----------------------------------------------------------
注解:刚开博客的时候就写了这道题,直接把代码搬过来了。
#include<iostream> #include<cmath> #include<stdio.h> using namespace std; int cNumber,Max,i,temp; char symbol; int main() { scanf("%d %c",&cNumber,&symbol); for(i = 1;;i++) { temp = 2*i*i+4*i; if(temp > cNumber-1) break; Max = temp; } for(temp = 2*(i-1);temp>=0;temp--) { for(int count = i-1;count != abs((i-1)-temp);count--) printf(" "); for(int count = 0;count<2*abs(temp-i+1) + 1;count++) printf("%c",symbol); printf("\n"); } printf("%d",cNumber-Max-1); return 0; }
------------------------------------------------L1-003----------------------------------------------------------
个位数统计
给定一个 k 位整数 N=dk−110k−1+⋯+d1101+d0 (0≤di≤9, i=0,⋯,k−1, dk−1>0),请编写程序统计每种不同的个位数字出现的次数。例如:给定 N=100311,则有 2 个 0,3 个 1,和 1 个 3。
输入格式:
每个输入包含 1 个测试用例,即一个不超过 1000 位的正整数 N。
输出格式:
对 N 中每一种不同的个位数字,以 D:M 的格式在一行中输出该位数字 D 及其在 N 中出现的次数 M。要求按 D 的升序输出。
输入样例:
100311
输出样例:
0:2 1:3 3:1
------------------------------------------------L1-003----------------------------------------------------------
注解:简单签到题,思路就是分割位数之后存入大小为10的数组里叠加就行。
#include<stdio.h> #include<string.h> char temp[10001]; int length; int number[10]; int main() { scanf("%s",&temp); length = strlen(temp); for(int i = 0;i<length;i++) number[temp[i] - '0']++; for(int i = 0;i<10;i++) if(number[i] != 0) printf("%d:%d\n",i,number[i]); return 0; }
------------------------------------------------L1-004----------------------------------------------------------
计算摄氏温度
给定一个华氏温度F,本题要求编写程序,计算对应的摄氏温度C。计算公式:C=5×(F−32)/9。题目保证输入与输出均在整型范围内。
输入格式:
输入在一行中给出一个华氏温度。
输出格式:
在一行中按照格式“Celsius = C”输出对应的摄氏温度C的整数值。
输入样例:
150
输出样例:
Celsius = 65
------------------------------------------------L1-004----------------------------------------------------------
注解:题目简单,签到题,细节注意下浮点实型和实数的转换就好了。
#include<stdio.h> long long int temp; int main() { scanf("%lld",&temp); printf("Celsius = %d\n",int(5*(temp-32)/(9*1.0))); return 0; }
------------------------------------------------L1-005----------------------------------------------------------
考试座位号
每个 PAT 考生在参加考试时都会被分配两个座位号,一个是试机座位,一个是考试座位。正常情况下,考生在入场时先得到试机座位号码,入座进入试机状态后,系统会显示该考生的考试座位号码,考试时考生需要换到考试座位就座。但有些考生迟到了,试机已经结束,他们只能拿着领到的试机座位号码求助于你,从后台查出他们的考试座位号码。
输入格式:
输入第一行给出一个正整数 N(≤1000),随后 N 行,每行给出一个考生的信息:准考证号 试机座位号 考试座位号。其中准考证号由 16 位数字组成,座位从 1 到 N 编号。输入保证每个人的准考证号都不同,并且任何时候都不会把两个人分配到同一个座位上。
考生信息之后,给出一个正整数 M(≤N),随后一行中给出 M 个待查询的试机座位号码,以空格分隔。
输出格式:
对应每个需要查询的试机座位号码,在一行中输出对应考生的准考证号和考试座位号码,中间用 1 个空格分隔。
输入样例:
4 3310120150912233 2 4 3310120150912119 4 1 3310120150912126 1 3 3310120150912002 3 2 2 3 4
输出样例:
3310120150912002 2 3310120150912119 1
------------------------------------------------L1-005----------------------------------------------------------
注解:签到题,思路就是构造一个结构体,因为座位不会跳着安排,只要按结构体sort排序一下,取相应位置就直接出来了。
#include<stdio.h> #include<algorithm> using namespace std; int N,M; struct Stu{ char id[17]; int test; int pos; }Student[1000]; int cmp(Stu a,Stu b) { return a.test<b.test; } int main() { scanf("%d",&N); for(int i = 0;i<N;i++) scanf("%s %d %d",&Student[i].id,&Student[i].test,&Student[i].pos); sort(Student,Student+N,cmp); scanf("%d",&M); for(int i = 0;i<M;i++) { int temp; scanf("%d",&temp); printf("%s ",Student[temp-1].id); printf("%d\n",Student[temp-1].pos); } return 0; }
------------------------------------------------L1-006----------------------------------------------------------
连续因子
一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3×5×6×7,其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N,要求编写程序求出最长连续因子的个数,并输出最小的连续因子序列。
输入格式:
输入在一行中给出一个正整数 N(1<N<231)。
输出格式:
首先在第 1 行输出最长连续因子的个数;然后在第 2 行中按 因子1*因子2*……*因子k 的格式输出最小的连续因子序列,其中因子按递增顺序输出,1 不算在内。
输入样例:
630
输出样例:
3 5*6*7
------------------------------------------------L1-006----------------------------------------------------------
注解:这道题才是我今天要着重讲一下滴~ 一上来懵了一下,突然不知道怎么处理因式分解,一开始的思路就是一个for循环从头一直除到尾,结果发现样例都过不了,这种题跟很早我在说想要研究的因式分解题类似,寻思着如何获得所有的因式。这个是后面的话了,先来解决一下这道题:
· 代码分块:
第一步:套用素数识别公式:
bool judge(int x){ for(int i=2;i<sqrt(x);i++) if(x%i==0) return false; return true; }
先判断输入的数是否是素数,进行一下特判,因为是素数的话就直接输出1和本身的数就好了~
第二步:核心模块:
for(int i = 2;i<=sqrt(temp);i++) { temp_num = 1; for(int j = i;j*temp_num<=temp;j++) { temp_num*=j; if(temp % temp_num == 0 && j-i+1 > ans) { ans = j-i+1; temp_count = i; } } }
外层for来启动start数,就是从哪开始整除,temp_num实际上就是第二层for连续积,同时第二层的for在连续积在输入的数范围内,然后不断判断输入的数能否整除temp_num,而j-i+1实际上就是获取到连乘数的长度。
第三步:输出
for(int i = 0;i<ans;i++) { printf("%d",temp_count+i); if(i!=ans-1) printf("*"); else printf("\n"); }
· AC代码:
#include<stdio.h> #include<math.h> unsigned long long int temp; int temp_num,temp_count,ans; bool judge(int x){ for(int i=2;i<sqrt(x);i++) if(x%i==0) return false; return true; } int main() { ans = 0; temp_count = 0; scanf("%d",&temp); if(judge(temp)){ printf("1\n%d",temp); return 0; } for(int i = 2;i<=sqrt(temp);i++) { temp_num = 1; for(int j = i;j*temp_num<=temp;j++) { temp_num*=j; if(temp % temp_num == 0 && j-i+1 > ans) { ans = j-i+1; temp_count = i; } } } printf("%d\n",ans); for(int i = 0;i<ans;i++) { printf("%d",temp_count+i); if(i!=ans-1) printf("*"); else printf("\n"); } return 0; }
· 解后反思:
刚刚提到一个问题就是说,如何列出一个数的所有因式,这里引出另外一道题:
输入一个数,输出其所有的可能的因式分解方式:(可重复)
本质:使用DFS深搜得到 AC代码:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; int n,ans=0,j=0,a[1000000]={0},temp; int su(int x)//判断素数 { if(x==1||x==2)return 1; for(int i=2;i<=sqrt(x);i++) if(x%i==0)return 0; return 1; } void dfs(int x) { if(x==n) { cout<<" = "<<n<<"\n"; temp = 0; ans++; return; } else if(x>n)return; else { for(int i=0;i<j;i++) { if(x*a[i]>n)break; if(n%(x*a[i])==0) { if(temp != 0) cout<<" * "; if(temp == 0) if(x!=1) cout<<x<<" * ",temp = 1; if(temp != 0) cout<<a[i]; dfs(x*a[i]); } } } } int main() { while(cin>>n) { if(su(n)); else { for(int i=2;i<=n/2;i++) { if(n%i==0) a[j++]=i; } temp = 0; dfs(1); } cout<<n<<" * 1 = "<<n<<endl; } return 0; }
使用示范:
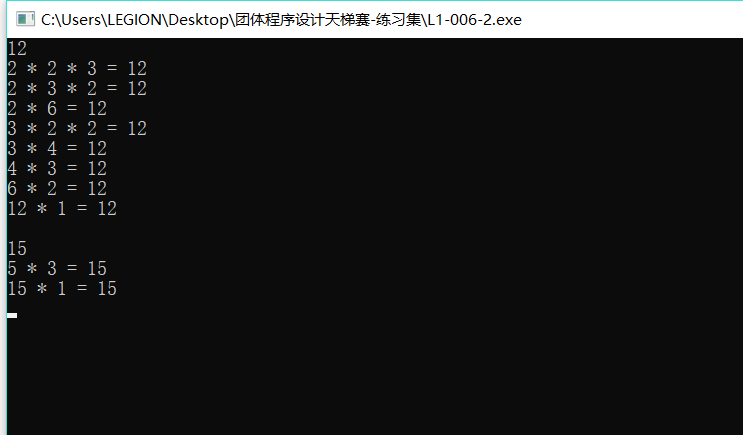
注解:这种深搜DFS方式值得品味思考,能够给今后的因式分解找到最优解有极大帮助,希望能分享给有用的人。
注:如果有更好的解法,真心希望您能够评论留言贴上您的代码呢~互相帮助互相鼓励才能成长鸭~~



