『嗨威说』数据结构的基本概念和术语、算法分析的时间复杂度(深度剖析)
『嗨威说』这是我第一篇博客,打开了我码农记录学习的新篇章,在之前学习C++、Java、Python的过程中都没有将自己的学习历程记录下来,是一大遗憾,但如今,在2019.02.22这一天,开通了博客并写下了第一篇博客,就希望将写博客这一行为养成习惯坚持下去。
大一下开了《数据结构》这门课程,开始深入涉及数据的构和算法的学习,算是打牢地基的必要操作,早在很早制作一些单机游戏的时候,早有对时间复杂度的一个浅显认知,当我所写的算法十分冗长时,编译出来的ddl放入游戏引擎去执行的时候,启动游戏时间和游戏的流畅度就受到了大大影响,这是我最初刚认识到需要一个特别优质高效算法的重要性的一刻。下面就开始整理一下基本的概念和深度剖析时间复杂度的一些计算方式。
因为还只是大一初学打地基阶段,小小萌新,如果有任何错误,请大佬们指正点拨。
今日兴趣新闻:
《流浪地球》破40亿,深度对话刘慈欣:后续到底是怎么样的?
https://mbd.baidu.com/newspage/data/landingsuper?context=%7B"nid"%3A"news_9415719750552098400"%7D&n_type=1&p_from=4
数据结构的基本概念及术语
(一) 数据的基本概念:
数据——是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中边被计算机程序处理的符号的总称。
数据元素——数据的基本单位,在计算机程序中通常做为一个整体进行考虑和处理。
数据项——是组成数据元素的、有独立含义的、不可分割的最小单位。
数据对象——是性质相同的数据元素的集合,是数据的一个子集。
数据结构——是相互之间存在一种或多种特定关系的数据元素的集合。
逻辑结构——数据元素之间的逻辑关系的描述,它与数据的存储无关,是独立于计算机的。称为数据的逻辑结构。
存储结构——数据结构在计算机中的表示称为数据的物理结构,又称存储结构。
抽象数据类型 ——一般指由用户定义的、表示应用问题的数学模型,以及定义在这个模型上的一组操作的总称。
补充算法的一些特性:
算法特性:有穷性、确定性、可行性、输入和输出。
算法优劣的评价方式:正确性、可读性、健壮性、高效性。
(二) 数据结构的基本分类
1、逻辑结构
两个关键要素:数据元素、关系
用一张图就可以很好的说明逻辑结构的层次:
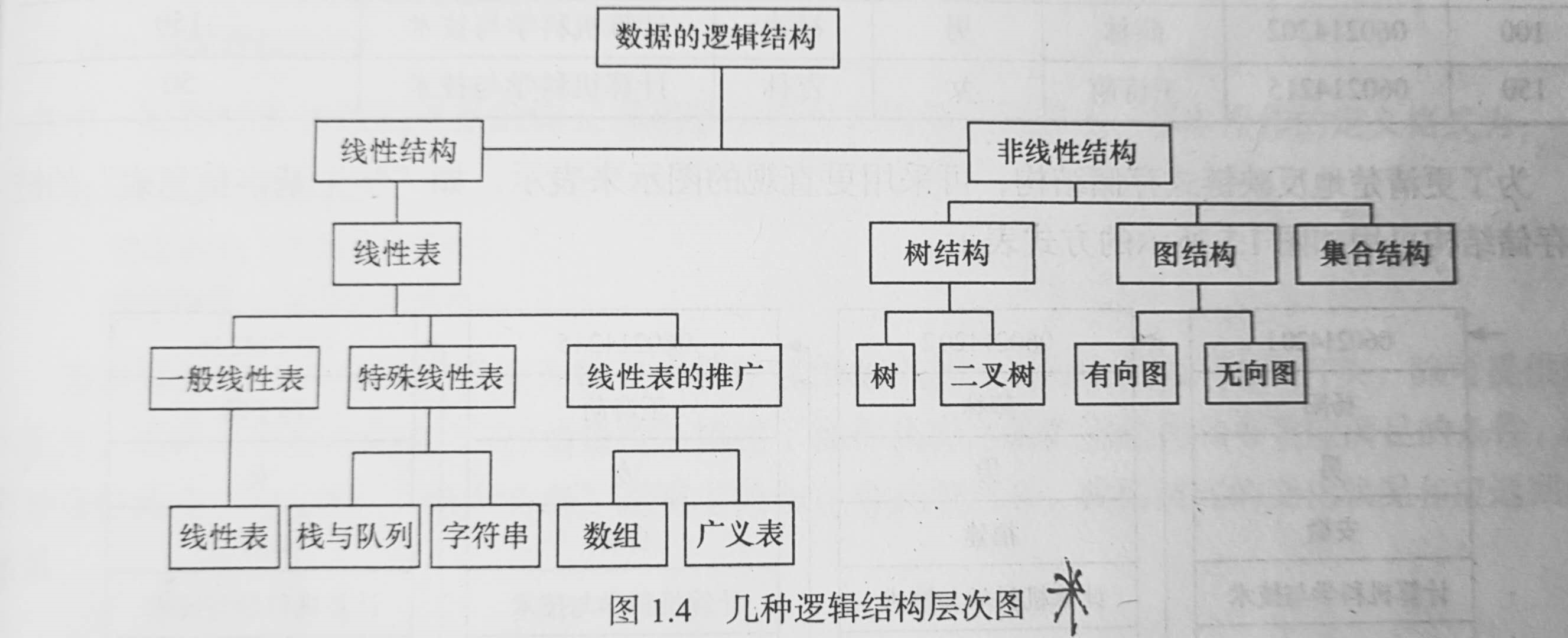
注:1、与数据元素本身的形式、内容、相对位置、个数无关的是数据的逻辑结构。
2、通常要求同一逻辑结构中的所有数据元素具有相同的特性,这意味着不仅数据元素所包含的数据项的个数要相同,而且对应数据项的类型要一致。
3、特别的,一些表面上很不同的数据可以有相同的逻辑结构。
2、存储结构 ( 物理结构 )
(1)顺序存储结构:简单说:就是存储器中相连的一块存储区域存放该数据,通常借助“数组”类型来实现。
(2)链式存储结构:简单说,就是存储在存储器中不同的区域中,不需要占用存储区一片连续的存储空间中,通常借助“指针”类型来实现。
算法的时间复杂度
在接触各式各样的算法之前,特别是学习数据结构之前,都会先涉及算法的两种复杂度,一种是时间复杂度,另一种是空间复杂度,随着存储技术的升级,基本电脑都可以达到1T以上的硬盘、8G以上的内存,所以基本不用担心空间复杂度的问题,所以对于时间复杂度的处理就成为了人们对算法高效性的最大评估标准,所以在这只讲时间复杂度,就不涉及空间复杂度了。
(一) 时间复杂度的基本概念:
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度(O是数量级的符号 ),简称时间复杂度。
说的挺复杂的样子,其实很简单,就是找到对算法运行时间影响最大的最初等基本函数,如:n、n^2、log(2)n之类。
(二) 时间复杂度的基本计算方法:
(1)计算出基本操作的执行次数T(n)
基本操作即算法中的每条语句(以;号作为分割),语句的执行次数也叫做语句频度(专业术语)。在做算法分析时,一般默认为考虑最坏的情况。
(2)计算出T(n)的数量级
无视常量、低次幂和最高次幂的系数,直接令f(n)=T(n)的数量级。
(3)用大O来表示时间复杂度
当n趋近于无穷大时,如果lim(T(n)/f(n))的值为不等于0的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))。
[例题]求下列算法的时间复杂度:
for(int i = 1;i<=n;i++) //频度为n+1 { for(int j = 1;j<=n;j++) //频度为n*(n+1) { c[i][j] = 0 //频度为n^2 for(int k = 1;k<=n;k++) //频度为(n^2)*(n+1) c[i][j] = c[i][j] + a[i][k]*b[k][j] //频度为n^3 } }
解答:
f(n)即为所有语句频度之和,得出f(n) = 2n3+3n2+2n+1,然后无视常量和各个系数得到:f(n) = n3+n2+n,即可取O(n3)
通过同阶无穷大的方式进行验算:lim(n3+n2+n)/n3当n→∞时,结果为2,为不等于0的常数,说明f(n)和n3为同阶无穷大,即可使用该复杂度。
注:
1、最坏时间复杂度:算法的时间复杂度不仅与语句频度有关,还与问题规模及输入实例中各元素的取值有关。一般不特别说明,讨论的时间复杂度均是最坏情况下的时间复杂度。保证了算法的运行时间不会比任何更长。
2、即求对数值(log),默认底数为10,简单来说就是“一个数用标准科学计数法表示后,10的指数”。例如,5000=5x10 3 (log5000=3) ,数量级为3。另外,一个未知数的数量级为其最接近的数量级,即最大可能的数量级。
3、求极限时要利用好1/n。当n趋于无穷大时,1/n趋向于0。
4、乘法法则:T(n,m) = T1(n) * T2(m) = O (f(n) * g(m))
5、任何非0正常数都属于同一数量级,记为O(1)。
(三) 常见的时间复杂度:
c < log2n < n < n*log2n < n2 < n3 < 2n < 3n < n! (c是一个常量)
|--------------------------|--------------------------|-------------|
较好 一般 较差
| 执行次数函数 | 阶 | 术语描述 |
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n2+2n+1 | O(n2) | 平方阶 |
| 5log2n+20 | O(log2n) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlog2n阶 |
| 6n3+2n2+3n+4 | O(n3) | 立方阶 |
| 2n | O(2n) | 指数阶 |
(四)时间复杂度的一些常见示例说明:
====>O(1) —— 常数阶
temp=i; i=j; j=temp;
以上三条单个语句的频度均为1,该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶,记作T(n)=O(1)。
注意:如果算法的执行时间不随着问题规模n的增加而增长,即使算法中有上千条语句,其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。
====>O(n2) —— 平方阶(立方阶、线性阶同理)
sum=0; //(语句频度为:1) for(i=1;i<=n;i++) //(语句频度为:n+1) for(j=1;j<=n;j++) //(语句频度为:n^2) sum++; //(语句频度为:n^2)
解:因为Θ(2n2+n+1)=n2(Θ即:去低阶项,去掉常数项,去掉高阶项的常参得到)
注意:一般情况下,对步进循环语句只需考虑循环体中语句的执行次数,当有若干个循环语句时,算法的时间复杂度是由嵌套层数最多的循环语句中最内层语句的频度f(n)决定的。
====>O(log2n) —— 对数阶
int count = 1; while(count < n){ count = count * 2; }
解:因为每次count*2后,距离结束循环更近了。也就是说有多少个2 相乘后大于n,退出循环。数学公式:2x = n --> x = log2n
因此这个循环的时间复杂度为O(log2n)
(五)一些复杂情况的时间复杂度分析:
=====>并列循环的复杂度分析:
for (i=1; i<=n; i++) x++; for (i=1; i<=n; i++) for (j=1; j<=n; j++) x++;
解:
第一个for循环
T(n) = n
f(n) = n
时间复杂度为Ο(n)
第二个for循环
T(n) = n2
f(n) = n2
时间复杂度为Ο(n2)
整个算法的时间复杂度为Ο(n+n2) = Ο(n2)。
=====>函数调用的复杂度分析:
public printsum(int count){ int sum = 1; for(int i= 0; i<n; i++){ sum += i; } cout<<sum<<endl; }
解:只有可运行的语句才会增加时间复杂度,因此,上面方法里的内容除了循环之外,其余的可运行语句的复杂度都是O(1)。
所以printsum的时间复杂度 = for的O(n)+O(1) = 忽略常量 = O(n)
优化方法:
public printsum(int count){ int sum = 1; sum = count * (count+1)/2; cout<<sum<<endl; }
这样时间复杂度就降为O(1)了。
我的这种时间复杂度分析是根据书本最经典的方法,即时间频度求和的函数分析法,在网上游览一些资料的时候还发现了一种时间复杂度的分析方法,就是直接取最大值法,但其实两种方法本质是完全一致的,只是后者使用会更加方便一些,附上参考链接:https://www.jianshu.com/p/f4cca5ce055a。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号