【学习笔记】斜率优化

【学习笔记】斜率优化

[SDOI2012]任务安排

斜率优化入门题：

设\(f(x)\)为\(F(x)\)的后缀和，\(t(x)\)为\(T(x)\)的前缀和。\(dp(i)\)表示完成到第\(i\)任务的最小代价，转移：

\(dp(i)=\min \{dp(j) +f(j+1)\times(S+t(i)-t(j)) \}\)

拆掉：

• 和\(j\)无关: 没有
• 只和\(j\)相关:\(dp(j)+f(j+1)\times(S-t(j))\)
• 和\(i,j\)相关:\(f(j+1)\times t(i)\)

我们发现只和\(j\)相关的可以直接预处理，现在的问题是确定了\(i\)如何快速找到一个\(j\)

令\(y_j=dp(j)+f(j+1)\times(S-t(j))\)，\(x_j=f(j+1)\)，原式可以写成：

\[dp(i)= y_j+x_jt(i) \]

转换一下式子

\[y_j=-t(i)x_j+dp(i) \]

现在问题就变成了确定了一个\(i\)，要快速查询前面的一个\(j\)使得\(dp(i)\)最小

把这个东西看成一条直线，就变成了我有一条在平面上平移的斜率为\(-t(i)\)的直线，现在要找一个点\((x_j,y_j)\)使得过这个点的斜率为\(-t(i)\)的直线的截距尽量小。

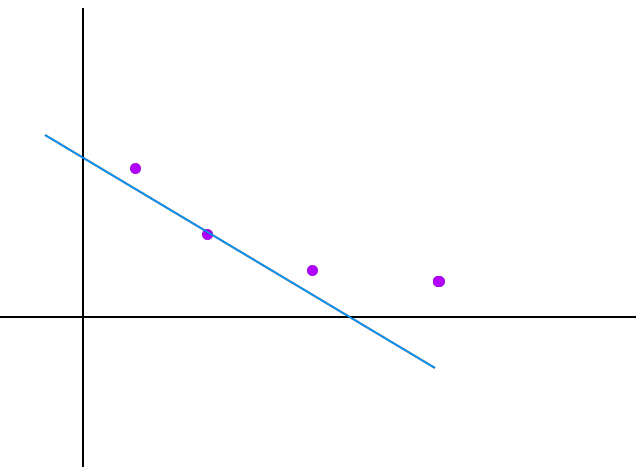
蓝线:斜率为\(-t(i)\)的线

紫点:\((x_j,y_j)\)

很明显，可以看做有一条在\(y\)负半轴无限远处有一条直线慢慢上移(截距慢慢变大)，这条直线突然经过一个我们集合内的点时，它此时的截距就是最小的截距。很显然，这个点一定在凸包上面，而且这个点左右两边的斜率一定是左边更小，右边更大(斜率是负数)。

动态维护一下凸包就好了。

//@winlere
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;  typedef long long ll;
inline int qr(){
      register int ret=0,f=0;
      register char c=getchar();
      while(c<48||c>57)f|=c==45,c=getchar();
      while(c>=48&&c<=57) ret=ret*10+c-48,c=getchar();
      return f?-ret:ret;
}
int n,s;
const int maxn=3e5+5;
int Ti[maxn],Fi[maxn];
ll st[maxn],sf[maxn];
ll x[maxn],y[maxn],q[maxn],dp[maxn];
int cnt;

inline ll getval(const int&i,const int&j){
      return dp[j]+sf[j+1]*(s+st[i]-st[j]);
}

inline bool chek0(const int&i,const int&j,const ll&k){
      return (long double)1.0*((y[i]+dp[i])-(y[j]+dp[j]))*(x[i]-x[k])<=(long double)1.0*((y[i]+dp[i])-(y[k]+dp[k]))*(x[i]-x[j]);
}

inline bool chek(const int&i,const int&j,const ll&k){
      return (long double)1.0*(y[i]+dp[i])-(y[j]+dp[j])<=(long double)1.0*k*(x[i]-x[j]);
}

inline int lookup(const ll&k){
      register int l=1,r=cnt-1,ret=cnt,mid;
      while(l<=r){
	    mid=(l+r)>>1;
	    if(chek(q[mid],q[mid+1],k))
		  r=mid-1,ret=mid;
	    else l=mid+1;
      }
      return q[ret];
}
int main(){
      
      n=qr();s=qr();
      for(register int t=1;t<=n;++t)
	    Ti[t]=qr(),Fi[t]=qr(),st[t]=st[t-1]+Ti[t];
      for(register int t=n;t>=0;--t) sf[t]=sf[t+1]+Fi[t];
      for(register int t=0;t<=n;++t) y[t]=sf[t+1]*(s-st[t]),x[t]=sf[t+1];
      q[cnt=1]=0;
      for(register int t=1;t<=n;++t){
	    dp[t]=getval(t,lookup(-st[t]));
	    while(cnt>1&&chek0(q[cnt-1],q[cnt],t)) --cnt;
	    q[++cnt]=t;
      }
      cout<<dp[n]<<endl;
      return 0;
}

D - Cats Transport

\(O(n^2)\)的转移：

\[dp(i,j)=\min\{dp(i-1,j),dp(i-1,k)+(j-k)\times t_j-(sum(j)-sum(k))\} \\ sum(i)=\Sigma_{j=1}^it_j-dis(1,j) \]

拆开\(j,k\)直接变成一个斜率优化的套路式。

\(x_k=k,y_k=dp(i-1,k)+sum(k)\)

原式变为:

\[y_k=t_jx_k+(dp(j)-j\times dis(1,j)+sum(j)) \]

查询一个截距最小值。好像要单调队列维护。查到哪个\(k\)转移套到原式就好了。

不过这里复杂度貌似\(O(n)(k\le 100)\)

//@winlere
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;  typedef long long ll;
inline ll qr(){
      register ll ret=0,f=0;
      register char c=getchar();
      while(c<48||c>57)f|=c==45,c=getchar();
      while(c>=48&&c<=57) ret=ret*10+c-48,c=getchar();
      return f?-ret:ret;
}
const int maxn=1e5+5;
int n,m,p;
int dis[maxn];
ll sumd[maxn];
ll sumdata[maxn];
ll x[maxn];
ll y[maxn];
ll dp[101][maxn];
struct NODE{
      int pos,time;
      ll limit;
      NODE(){limit=pos=time=0;}
      inline bool operator <(const NODE&a)const{return limit<a.limit;}
      inline void scan(){
	    pos=qr();time=qr();
	    limit=time-sumd[pos];
      }
}data[maxn];


typedef deque<int>::iterator it;
deque < int > q;

int main(){
      
      n=qr();m=qr();p=qr();
      for(register int t=2;t<=n;++t)
	    sumd[t]=(dis[t]=qr())+sumd[t-1];
      for(register int t=1;t<=m;++t)
	    data[t].scan();
      sort(data+1,data+m+1);
      for(register int t=1;t<=m;++t) sumdata[t]=data[t].limit+sumdata[t-1];
      memset(dp,5,sizeof dp);
      dp[0][0]=0;
      it ita;
      for(register int i=0;i<=m;++i)
	    x[i]=i;
      for(register int t=1;t<=p;++t){
	    for(register int i=0;i<=m;++i){
		  dp[t][i]=dp[t-1][i];
		  y[i]=dp[t-1][i]+sumdata[i];
	    }
	    q.clear();
	    for(register int i=1;i<=m;++i){
		  q.push_back(i-1);
		  ita=q.begin();
		  while(q.size()>1&&y[*(ita+1)]-y[*ita]<=1ll*data[i].limit*((*(ita+1))-(*ita))) q.pop_front(),ita=q.begin();
		  register int j=q.front();
		  dp[t][i]=min(dp[t][i],dp[t-1][j]+1ll*(i-j)*data[i].limit-(sumdata[i]-sumdata[j]));
		  ita=q.end()-1;
		  while(q.size()>1&&(y[*ita]-1ll*y[*(ita-1)])*(i-(*ita))>=1ll*(y[i]-y[*ita])*((*ita)-(*(ita-1)))) q.pop_back(),ita=q.end()-1;;
	    }
      }
      cout<<dp[p][m]<<endl;
      return 0;
      
}

参考文献：

瓦努霍格木茨格兰芬多神威无敌无双超神大聚聚yyb的博客