数据实践过程中理论总结
写在前面(常规啰嗦)
拖拖拉拉新的一年已经过去一个月,今天3月6号。月底离职去平安,想来已经在这家公司呆了整整两年,对比两年前的我工程上确实大有长进,理论方面好像并没有得到很好的拓展,希望下一家能够得到比较好的历练。23岁,一个也算是比较尴尬的年纪,青春是很容易混过去的,尤其是工作以后,于是想继续深造读书,考了几次也实在是分数丢人哈哈,或许是不应该执拗在中科院这一个学校,再接再厉,考虑深圳其他学校也未必不是好的解决方案。
言归正传,今天总结的是过去两年大数据分析中的理论概括,有经常做的滚瓜乱熟的数据清洗,数据分析,一般算法应用,也有正在探索的数据准确性成套解决方案的探索。实际应用中,我们往往关心的是,你算出的数据到底准不准?有多大的可信度?这两个问题是任何一个负责任的数据工程师都必须做到问心无愧的回答,很难但是又很有必要。
第一部分:数据质量评估
作为一个数据工程师,拿到第一手原始数据的时候,我们会接触到数据的基本内容和字段介绍,我们会想到数据文件大小是否合理(数据对比以往是多了还是少了还是正常大小),数据的必要字段和非必要字段的识别及其对应的基本的描述性统计,说道描述性统计,非统计学出身的胖友们可能需要了解一下统计量的定义。
- 统计量的定义

举一个例子,例如深圳通刷卡数据。假设一年的深圳通刷卡数据是一个总体,此时我想要知道深圳通一周维度上的客流量变化,假设不做集群计算,一年几百G的数据对于短时间使用单机计算确实是够折腾。这个时候我们选择抽样方法,抽取每个月中第一周的数据作为样本。然后对这些样本数据取平均值得到深圳通刷卡客流量平均一周的数据变化,这里的平均值就属于我们统计学中的统计量。那么什么是统计量呢,常用的统计量有哪些呢?
- 常用的统计量
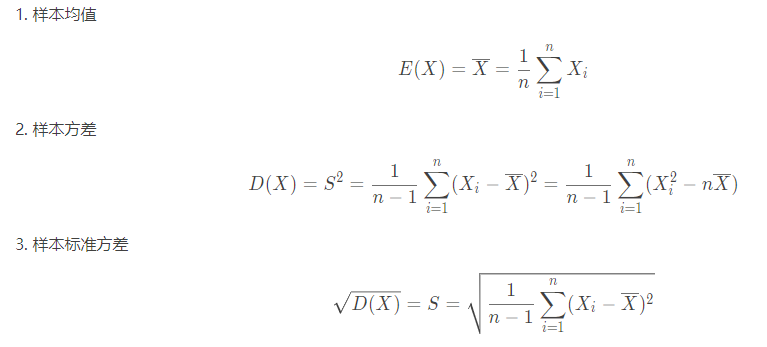
这里需要了解的是我们在实际数据分析中用的统计量往往不止于这些,甚至是我们需要用到多个统计量综合来考量数据的总体性质。比如,对于分布均匀的数据,我们只用平均值确实能够比较好的反映总体的数据分布情况;但对于两极分化比较严重的数据,平均值很容易受到极值的影响,这个时候就需要结合方差或者标准差来给数据总体情况定性;两极化分布严重的数据中,还有一种情况就是当大多数数据分布在两极,方差会比标准差更能反映数据的实际波动情况,而众数作为大多数数据的代表者或许也可以成为参考指标。
- 统计量在数据质量评估中的作用

上图是Spark对车辆GPS数据做的一个基本的统计描述截图,使用的是DataFrame中的describe方法。上如中横向列表中lon属于经度,lat属于纬度,speed属于行车瞬时速度,angle属于角度。纵向列表中分别是记录条数,平均值,标准差,最小值和最大值。可以看出经纬度数据始终是在一个合理范围内波动,标准差stddev都在1以下,而速度和角度的标准差就差很多,说明速度和角度的数据分布比较分散。这里,先介绍一般的数据质量评估步骤:
- 提取必要字段。以GPS数据为例,时间、经度、纬度、车辆ID为必要字段。
- 对必要字段做数据质量评估。数据变量分为离散变量和连续变量。例如车牌号作为离散变量就需要考虑其字符串格式的车牌号的完整性;连续变量中分为不可均值计算的时间字符串这样的非数值型的变量,做时间差计算的时候需要将数据格式化解析处理,因此也必须保证时间字符串的格式的正确性和有效性;经纬度这样的数据就可以直接用来做一般的描述性统计分析,保证定位的合理性。
第二部分:数据清洗
数据清洗实际上是一个承上启下的步骤。根据前面的数据质量评估结果选择适当的清洗规则,这一个步骤直接影响了后面数据分析的统计结果,需要谨慎处理异常值,那么什么是异常值呢。
- 异常值定义
异常值,即数据集中存在的不合理的值,又称为离群点。从集合角度来看,异常值即离群点,如下图所示:
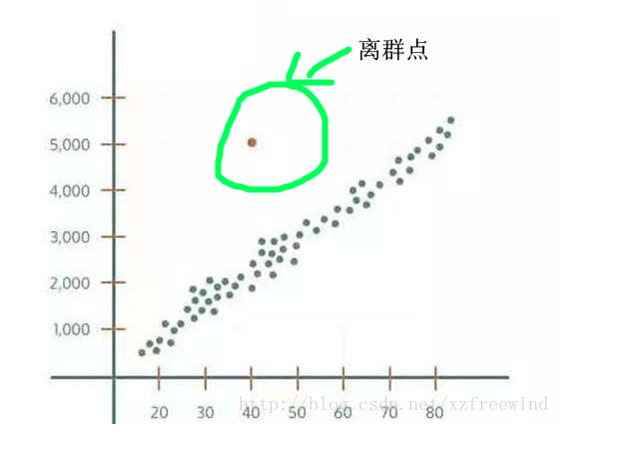
而实际情况往往复杂的多,异常点发生的情况往往是复杂的,具体情况具体分析。例如:你需要找出一个班上天赋秉异的学生,你就需要找出这样一个各方面都变现突出或者行为不符合一般规律的学生,这样的异常点就是你需要研究的对象;而对于定位数据中,有一段数据都出现在不该出现的地方,是不是考虑该车辆的司机有越界行驶的可能,这对司机和车辆的能起到基本的监督行为;而一般情况,一辆车一段规律的行车轨迹中只有一两个定位点是偏离原有的轨迹,这样的数据是不是可以考虑直接删除?而同样,如何去检测这些离群点,也是我们研究的主要内容。
- 异常值检验与常用的处理方法
异常检验:
- 简单统计分析:对属性做基本范围约束,并对数据做描述性统计分析,检测区间外的值。
- 3segma原则:当数据服从正态分布,距离平均值3segma(segma是正态分布函数标准差)之外的概率不大于0.003,这样的事件我们成为极小概率事件。因此,样本距离平均值大于3segma,则认定该样本为异常值。
- 箱线图分析:箱线图提供了一个识别异常值的标准,即大于或小于箱线图设定的上下值的数据记为异常值。计算上下四分位数,中位数以及均值。设上四分位数为U,下四分位数为L,IQR=U-R,上界为U+1.5IQR,下界为L-1.5IQR。
异常处理:
- 删除含有异常值的记录(该方法过于简单粗暴,仅适合明显无效的记录);
- 将异常值视为缺失值,按缺失值处理(如取平均值替代,时间序列模型中常用);
- 不处理(具体业务再处理或者直接将大规模异常数据上报,起监督的作用)。
第三部分:指标校验方法
数据清洗后,需要做大量的报表统计,计算出的一些指标,如何去保证其计算结果的准确性,这里介绍四种常规数据指标的校验方法。
- 与历史数据对比。最经典的方法就是针对同样的指标的计算结果与之前的计算结果对比,最常用到的是同比和环比;
- 交叉校验。交叉校验分为两种:一种是同一个数据源的不同指标之间的交叉验证,举例子可以想象某个站点的客流量必定是不小于该站点的进站量或者出站量。另外一种是不同数据源的相关指标验证,这里的相关指标指的是指标之间具有比较强的相关性,无论是正相关还是负相关都具有一定的参考意义,例如一个人的教育程度和其薪水是呈现正相关。
- 统计分布。一般的数据会符合正态分布或者伽马分布这样的规律(不仅限于这两种分布,例如早晚高峰,周末与工作日都会产生具有一定时序性的数据)。
第四部分:算法校验
大部分时候,脑子里描述的算法,就算在工程上实现了落地,没有在现实场景下产生实际效益,或者说要想检验在实际应用中产生的效果,还需要过实际应用的检验,毕竟实践是检验一切真理的唯一标准。这里我们需要涉及到抽样设计以及探讨一般的抽样步骤,仅仅是总结,具体实施方案因场景不同而灵活运用。
- 抽样类型
- 简单随机抽样。对于一个总体,如果通过逐个抽取的方法抽取样本,且每次抽取时,每个个体被抽到的概率相等,这样的抽样方法记为简单随机抽样。举个例子:暗箱里有10个球,每个球被摸到概率相同,逐个抽3个球。这里涉及到有放回随机抽样和无放回。其依据是是否在每次抽样之后将原来的球放回到暗箱里(当然,这里涉及到的总体都比较简单且少量单一的情况)。
- 系统抽样。当涉及到的总体比较多的时候,首先考虑把总体分成均衡的几个部分,然后按照预定的规则,从每一个部分中抽取一些个体,得到需要的样本,这样的方法为系统抽样。比如:班级上有40个学生,按照从1到39编号,首先随机抽取一个编号加入是3,然后设定一个抽样距离为10,那么下一个编号就是13,以此类推再下一个编号就是23,随后一个编号是33。这样抽取4个人,比直接从40个学生中抽4个人要省力一点,因为系统抽样只需要抽取第一批,后面一批按照预先预定好的规则(比如固定抽样距离)抽取样本即刻,因此也会才被称为等距抽样。
- 分层抽样。取样时,将总体分为互不交叉的层,然后按照一定的比例,从各层中独立抽取一定数量的个体,这种得到样本的方法为分层抽样。(适用于总体由差异明显的几部分组成)。举个例子:想要调查某个站点一天的客流数据变化,我们知道地铁站点这样的公共交通尤其是在一线城市是很能反映通勤行为的,因此客流具有明确的早晚高平峰的波动现象。我们不想一天都守在站点附近,可以抽取早上7点到9点(早高峰),12点到13点(平峰),6点到8点(晚高峰)这五个小时调查客流数据。
- 多段抽样。多段随机抽样,就是把从调查总体中抽取样本的过程分为多个阶段进行的抽样方法。例如我们想要了解深圳市不同行政区里街道的人口变化情况。我们可以分别从深圳十个行政区中随机抽取一个街道,然后调查街道里的人口变化,这种抽样方法适应于数据分布广泛且总体数量很大的情况。
- 偶遇抽样。指研究者根据实际情况,以自己方便的形式抽取偶然遇到的人或根据自己最方便的形式查找调查对象的方法。最经常遇到的是我们经常需要校验深圳通OD数据计算结果,直接拿公司10个关系好的员工的深圳通卡数据与计算结果对比,这样好处是方便,坏处是这些员工都是通勤用户,可能不具有代表性。
- 抽样步骤
假如我们需要了解我们的车辆实时到站算法(电子站牌)的准确性。涉及到哪些步骤去检验呢?
- 界定总体。首先,我们需要对总体范围做一个明确的界定,假如我们需要了解深圳市公交的电子站牌的准确性,我们需要知道我们的总体是深圳市公交到站数据。
- 制定抽样框。其次,收集总体中全部抽样单位的名单,并通过名单建立起供抽样的抽样框,落在实际问题上就是我们需要一份所有深圳市公交线路与车牌号的名单,以及对应的线路站点信息。
- 决定抽样方案。根据我们的场景,我们可以分别在10个行政区中分别随机抽取3个公交站,选择某个时间段跟踪这30个站点的车辆到站时间,并记录车辆的车牌号和线路号。
- 实际抽取样本。根据抽样方案严格执行。保证数据的准确性与真实性。
- 评估样本质量。我们需要知道我们抽取的样本是否具有一般性,普遍性。
这些东西暂时写到这里,后面可能有更高阶的统计知识介绍,也算是把三年前的专业知识捡起来,如有不妥欢迎指正。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号