【论文解读】How attentive are graph attention networks?

图注意力网络有多专注？

题目: How attentive are graph attention networks?

作者：S Brody, U Alon, E Yahav

单位：Israel Institute of Technology，Google DeepMind，Tabnine

摘要：图注意网络（Graph Attention Networks, GATs）是最受欢迎的图神经网络（GNN）架构之一，并被认为是图表示学习的最先进架构。在 GAT 中，每个节点根据自身的表示作为查询，对其邻居进行注意。然而，我们在本文中指出，GAT 计算的是一种非常有限的注意类型：注意分数的排序不依赖于查询节点。我们正式定义这种受限的注意类型为静态注意，并将其与一种更具表现力的动态注意区分开来。由于 GAT 使用静态注意机制，因此存在一些简单的图问题，GAT 无法表达：在一个可控的问题中，我们证明了静态注意阻碍了 GAT 甚至无法拟合训练数据。为了解决这一局限性，我们通过修改操作顺序，提出了一种简单的修正方案——GATv2，这是一种严格比 GAT 更具表现力的动态图注意变体。我们进行了广泛的评估，并证明在匹配参数开销的情况下，GATv2 在 12 个 OGB 和其他基准测试中优于 GAT。GATv2 已被整合到 PyTorch Geometric 库、Deep Graph Library 和 TensorFlow GNN 库中。

代码：https://github.com/tech-srl/how_attentive_are_gats

1、背景与动机

背景

图神经网络（GNN）提供了一种通用且高效的框架，用于从图结构化数据中学习，在数据可以表示为一组节点且预测依赖于节点之间的关系（即边）的领域中具有广泛的应用。

在GNN中，每个节点通过与其邻居的交互以迭代方式更新其状态。GNN的不同变体主要在于每个节点如何聚合并结合其邻居的表示与自身的表示。Velicković 等人率先提出了一种基于注意力的邻居聚合方法——图注意网络（GAT）。在 GAT 中，每个节点计算其邻居的加权平均值，选择其最相关的邻居。

动机

GAT 实际上并未计算动态注意力。GAT 仅计算出一种受限的“静态”注意力形式：对于任何查询节点，注意力函数相对于邻居的得分是单调（也就是说，注意力系数的排序对于图中的所有节点是相同的，并且与查询节点无关）。这一事实严重削弱了 GAT 的表达能力。

如图1所示，query节点为{q0, ..., q9} ， key节点为{k0, ..., k9} ，组成了完全无向图，图中的系数是顶点间的注意力系数。图1-a为GAT的表现，所有query（q0 至 q9）都主要关注第 8 个key (k8)。

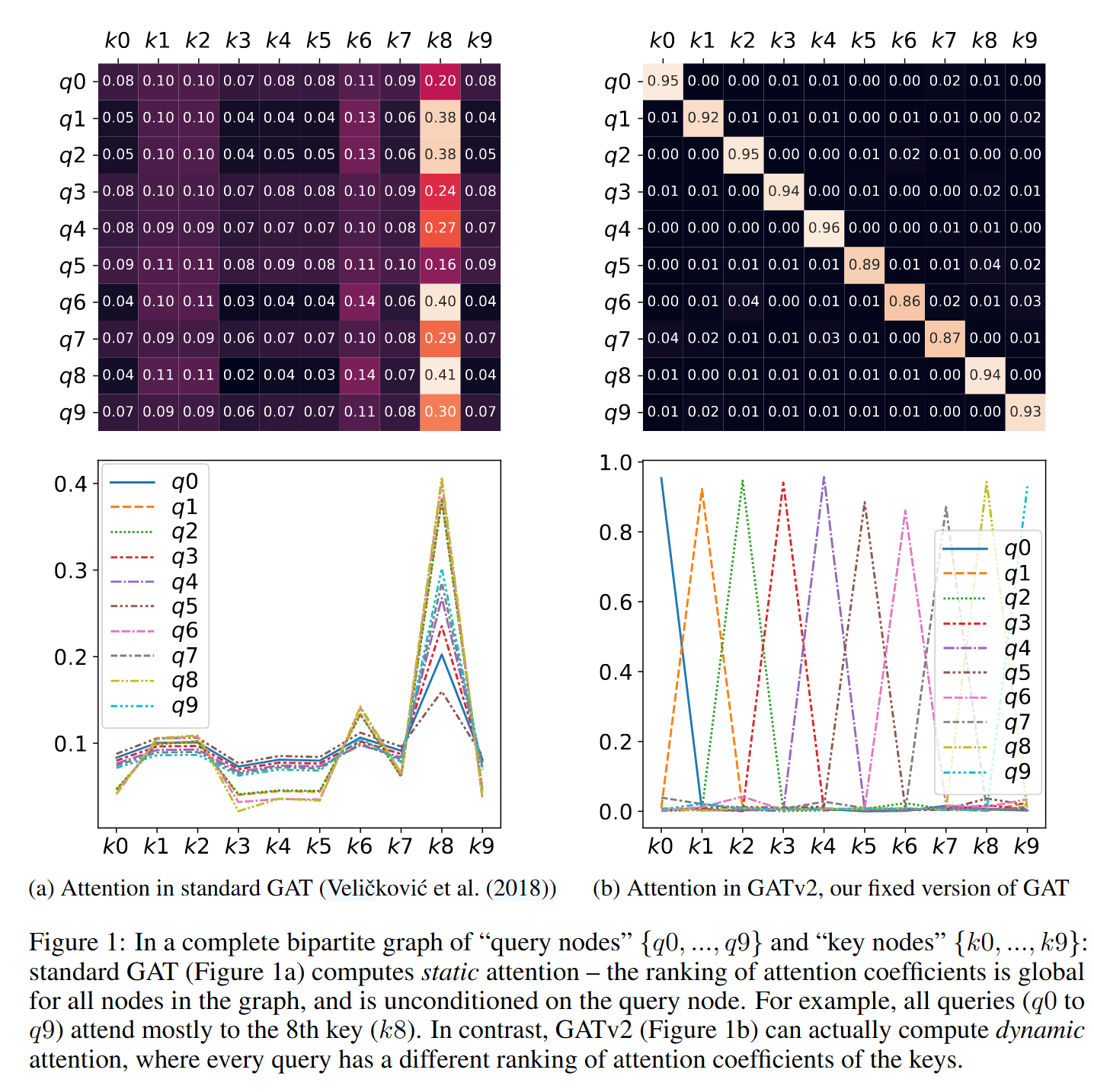
GATv2的主要贡献

指出了GAT只能计算静态注意力，即注意力权重的排序与查询节点无关。这种局限性使得GAT无法灵活地处理不同查询节点对邻居节点的重要性排序，从而限制了其表达能力。

GATv2通过修改GAT的内部操作顺序，将权重变换层（ $W$ ）放置在注意力计算前，并结合非线性函数。这一简单的调整使得GATv2能够计算动态注意力，即根据查询节点的不同动态调整邻居节点的重要性。论文通过数学证明，表明GAT只能计算静态注意力，而GATv2可以计算动态注意力，并成为一个通用注意力函数逼近器，其表达能力严格优于GAT。

2、预备知识

我们假设有向图 $G=(V,E)$ 每个节点 $i\in V$ 都有一个初始表示 $h_i^{(0)}\in {\mathbb{R}}^{d_0}$ 。每一层的输入是一组节点表示 $\{h_i\in {\mathbb{R}}^d|i\in V\}$ 和边的集合 $E$ 。

我们将一个神经架构（例如 GAT 的注意力函数）定义为一个由学习到的参数构成的函数族。函数族中的每个元素都是一个具有特定训练权重的具体函数。在以下部分中，我们使用 $[n]$ 表示集合 $[n]=\{1,2,...,n\}\subseteq \mathbb{N}$ 。

图注意力网络

GAT通过计算邻居表示的加权平均值实现了聚合操作。评分函数 $e:{\mathbb{R}}^d\times {\mathbb{R}}^d\to \mathbb{R}$ 为每条边 $(j,i)$ 计算得分，表示邻居 $j$ 的特征对于节点 $i$ 的重要性：

$$e(h_i,h_j)=\text{LeakyReLU}({\mathbf{a}}^{\mathrm{\top }}\cdot [W{h}_i\Vert W{h}_j])$$

其中， $\mathbf{a}\in {\mathbb{R}}^{2d^{\prime }}$ ， $W\in {\mathbb{R}}^{d^{\prime }\times d}$ 是学习得到的参数， $\Vert$ 表示向量拼接。注意力得分在所有邻居 $j\in N_i$ 上通过 softmax 正规化，注意力函数定义如下：

$${\alpha }_{ij}={\text{softmax}}_j(e(h_i,h_j))=\frac{\exp (e(h_i,h_j))}{\sum _{j^{\prime }\in N_i}\exp (e(h_i,h_{j^{\prime }}))}$$

GAT 通过邻居节点变换特征的加权平均值（结合非线性激活 $\sigma$ ）计算节点 $i$ 的新表示：

$$h_i^{\prime }=\sigma (\sum _{j\in N_i}{\alpha }_{ij}\cdot W{h}_j)$$

3、图注意力机制的表达能力

注意力机制是指根据输入键向量集合和附加查询向量计算一个分布。

3.1、GAT的局限性

如果注意力函数始终对某一个键向量的权重不小于其他任何键向量的权重，并且不依赖于查询向量，这种注意力函数为静态注意力。

静态注意力的定义：一个（可能是无限的）评分函数族 $\mathcal{F}\subseteq ({\mathbb{R}}^d\times {\mathbb{R}}^d\to \mathbb{R})$ 对于一组键向量集合 $\mathcal{K}=\{k_1,...,k_n\}\subseteq {\mathbb{R}}^d$ 和查询向量集合 $\mathcal{Q}=\{q_1,...,q_m\}\subseteq {\mathbb{R}}^d$ 计算静态评分。如果对于每个 $f\in \mathcal{F}$ ，都存在一个“最高评分”的键向量 $j_f\in [n]$ ，使得对于每个查询 $i\in [m]$ 和键向量 $j\in [n]$ ，都有 $f(q_i,k_{j_f})\ge f(q_i,k_j)$ 。我们称一个注意力函数集合在给定的 $\mathcal{K}$ 和 $\mathcal{Q}$ 下计算了静态注意力，如果其评分函数计算了静态评分，并可能后续结合了单调正规化（如 softmax）。

静态注意力的能力非常有限，因为每个函数 $f\in \mathcal{F}$ 都有一个始终被选择的键向量，而与查询无关。这样的函数无法建模不同键向量对不同查询相关性不同的情况。图 1-a 展示了静态注意力的情况。

GAT的局限性：GAT的设计目的是为每个节点计算其邻居的加权平均值作为表示。然而对于任何节点表示集合 $K=Q=\{h_1,...,h_n\}$ ，GAT层仅能计算静态注意力。证明如下：

证明：令 $G=(V,E)$ 是一个由GAT层建模的图，其参数 $a$ 和 $W$ 以及节点表示为 $\{h_1,...,h_n\}$ 。学习得到的参数 $a$ 可以写为连接的形式 $a=[a_1\parallel a_2]\in {\mathbb{R}}^{2d^{\prime }}$ ，其中 $a_1,a_2\in {\mathbb{R}}^{d^{\prime }}$ ，GAT的评分函数 $e$ 可以重写为：

$$e(h_i,h_j)=\text{LeakyReLU}(a_1^{T}W{h}_i+a_2^{T}W{h}_j)$$

由于 $V$ 是有限集，存在一个节点 $j_{\text{max}}\in V$ ，使得 $a_2^{T}W{h}_{j_{\text{max}}}$ 在所有节点中达到最大值（ $j_{\text{max}}$ 是静态注意力的定义中所需的 $j_f$ ）。由于LeakyReLU和softmax的单调性，对于每个查询节点 $i\in V$ ，节点 $j_{\text{max}}$ 同样会导致其注意力分布 $\{{\alpha }_{ij}|j\in V\}$ 的最大值。因此，直接从静态注意力的定义可以得出， $\alpha$ 仅计算静态注意力。这也意味着， $\alpha$ 无法计算动态注意力。

3.2、GATv2的提出与改进

动态注意力的定义：一个（可能是无限的）评分函数族 $\mathcal{F}\subseteq ({\mathbb{R}}^d\times {\mathbb{R}}^d\to \mathbb{R})$ 对于一组键向量集合 $\mathcal{K}=\{k_1,...,k_n\}\subseteq {\mathbb{R}}^d$ 和查询向量集合 $\mathcal{Q}=\{q_1,...,q_m\}\subseteq {\mathbb{R}}^d$ 计算动态评分，如果对于任意映射 $\varphi :[m]\to [n]$ ，都存在 $f\in \mathcal{F}$ ，使得对于任意查询 $i\in [m]$ 和键向量 $j\ne \varphi (i)\in [n]$ ，都有 $f(q_i,k_{\varphi (i)})>f(q_i,k_j)$ 。我们称一个注意力函数集合在给定的 $\mathcal{K}$ 和 $\mathcal{Q}$ 下计算了动态注意力，如果其评分函数计算了动态评分，并可能后续结合了单调正规化（如 softmax）。

也就是说，动态注意力可以使用查询 $i$ 选择每个键向量 $\varphi (i)$ ，通过使 $f(q_i,k_{\varphi (i)})$ 在集合 $\{f(q_i,k_j)|j\in [n]\}$ 中达到最大值。

标准GAT评分函数的主要问题在于学习到的权重层 $W$ 和注意力层 $a$ 是连续应用的，因此可以被压缩为单个线性层。为了解决这一限制，GATv2将注意力层 $a$ 应用在非线性激活函数（LeakyReLU）之后，而将权重层 $W$ 应用在向量拼接之后【例如 $[h_i\Vert h_j]$ 】，从而有效地通过多层感知机计算每个查询键对的评分。

公式如下：

• GAT (Velickovic et al., 2018)：

$$e(h_i,h_j)=\text{LeakyReLU}(a^T\cdot [W{h}_i\Vert W{h}_j])$$

• **GATv2 **：

$$e(h_i,h_j)=a^T\cdot \text{LeakyReLU}(W\cdot [h_i\Vert h_j])$$

GATv2的改进：一个 GATv2 层可以对任意节点表示集合 $K=Q=\{h_1,...,h_n\}$ 计算动态注意力。证明如下：

证明： 令 $G=(V,E)$ 表示由一个 GATv2 层建模的图，其节点表示为 $\{h_1,...,h_n\}$ 。令 $\phi :[n]\to [n]$ 为任意节点映射。我们定义函数 $g:{\mathbb{R}}^{2d}\to \mathbb{R}$ 如下：

$$g(x)=\{\begin{array}{ll}1,& \mathrm{\exists }i:x=[h_i\Vert h_{\phi (i)}]\\ 0,& \text{否则}\end{array}$$

接下来，我们定义一个连续函数 $\tilde{g}:{\mathbb{R}}^{2d}\to \mathbb{R}$ ，使得它仅在特定的 $n^2$ 个输入上等于 $g$ ：

$$\tilde{g}([h_i\Vert h_j])=g([h_i\Vert h_j]),\mathrm{\forall }i,j\in [n]$$

对于所有其他输入 $x\in {\mathbb{R}}^{2d}$ ，我们让 $\tilde{g}(x)$ 取任何保持连续性的值（这是可能的，因为我们仅固定了 $\tilde{g}$ 在有限点上的值）。

因此，对于每个节点 $i\in V$ 和 $j\ne \phi (i)\in V$ ：

$$1=\tilde{g}([h_i\Vert h_{\phi (i)}])>\tilde{g}([h_i\Vert h_j])=0$$

如果我们将两个输入向量连接起来，并将 GATv2 的评分函数 $e$ 定义为连接向量 $[h_i\Vert h_j]$ 的函数，根据通用近似定理， $e$ 可以逼近 $\tilde{g}$ 在 ${\mathbb{R}}^{2d}$ 的任何紧致子集上。

因此，对于任意足够小的 $ϵ$ （满足 $0<ϵ<\frac{1}{2}$ ），存在参数 $W$ 和 $a$ ，使得对于每个节点 $i\in V$ 和 $j\ne \phi (i)$ ：

$$e_{W,a}(h_i,h_{\phi (i)})>1-ϵ>0+ϵ>e_{W,a}(h_i,h_j)$$

并且由于 softmax 的递增单调性：

$${\alpha }_{i,\phi (i)}>{\alpha }_{i,j}$$

注：通常情况下，如果 GATv2 使用任何常见的非多项式激活函数，上述结果依然成立。

4、部分实验结果

4.1、合成任务：DictionaryLookup

任务设置：

• 设计一个简单的双分图任务来测试 GNN 的动态注意力能力。
• 下层节点包含字母属性和数值，上层节点仅包含字母属性，目标是根据共享的字母属性预测上层节点的数值。

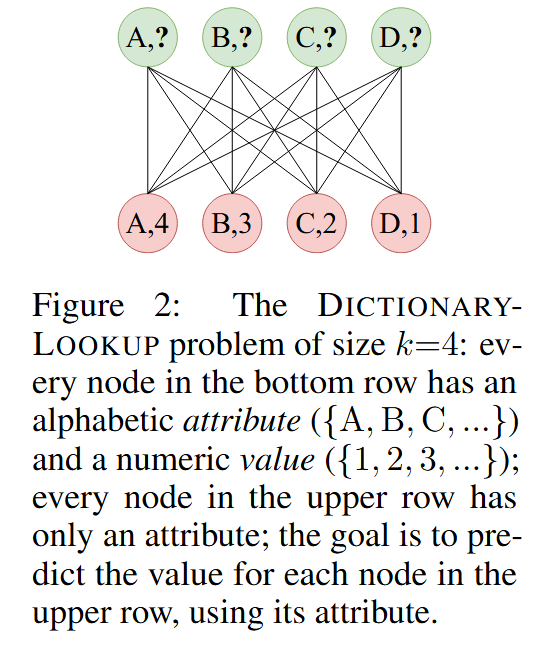
实验结果：

• GAT（单头）无法拟合训练集数据，多头 GAT 可以拟合训练集但在测试集上表现不佳。

• GATv2 在训练和测试集上均达到 100% 准确率，即使在复杂设置（如 k=100）下，使用单个注意力头也能解决问题。

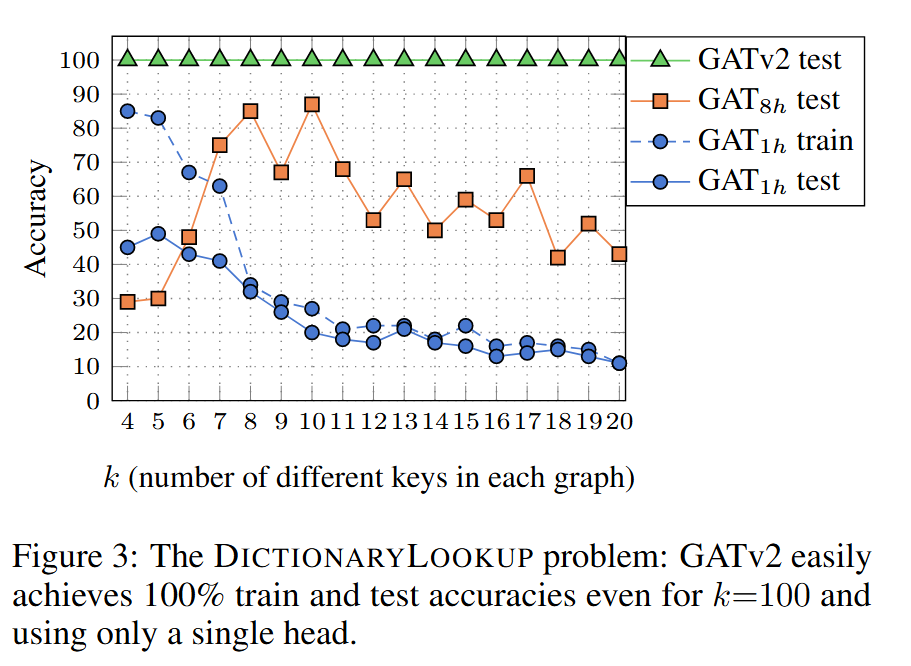
4.2、噪声鲁棒性

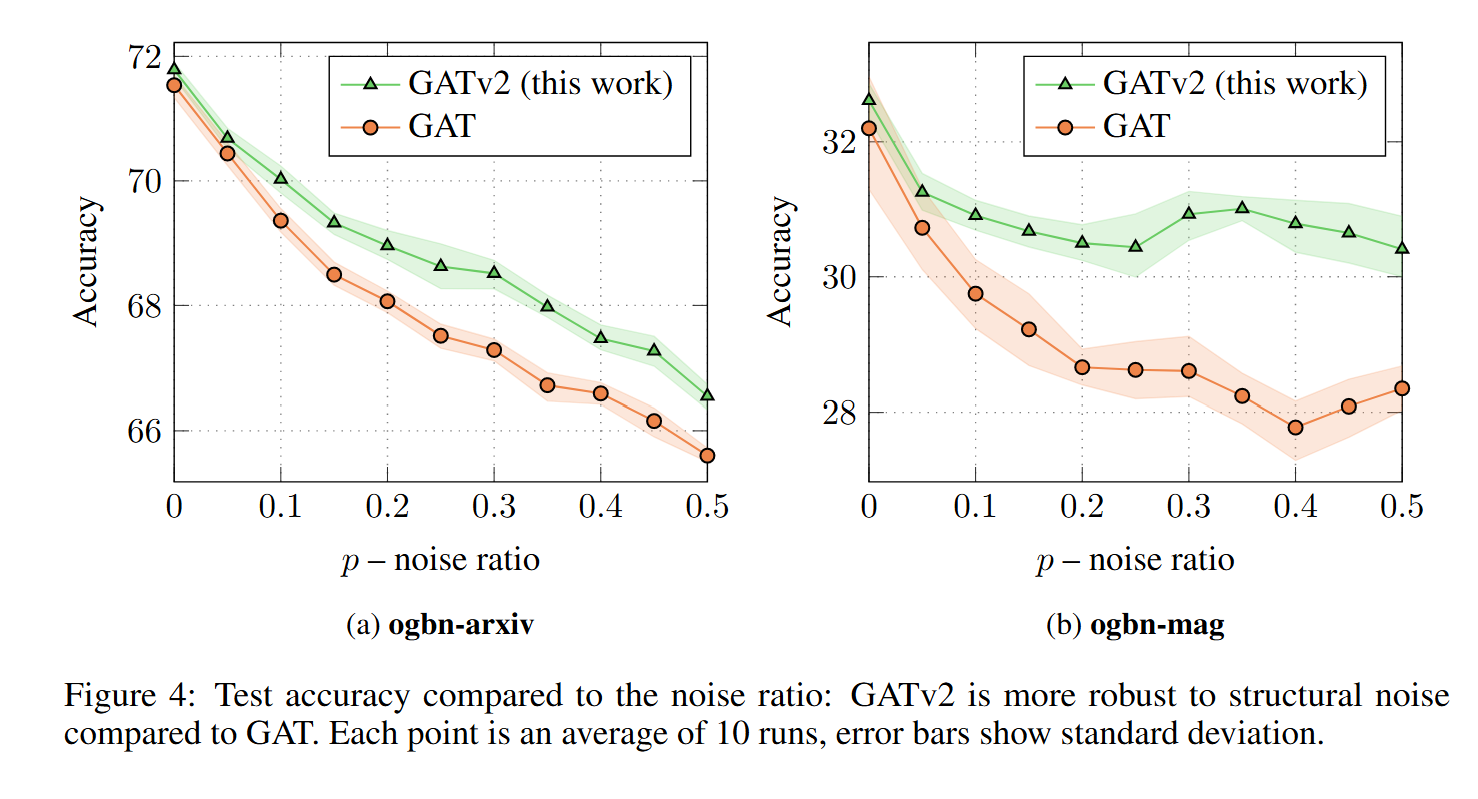
图4显示了两个来自开放图基准（OGB）的节点预测数据集的准确率随噪声比率 $p$ 的变化情况。

4.3、其他实验

在12个基准任务（包括节点分类、链接预测和图级别预测）上的广泛实验证明，GATv2在所有任务中性能均优于GAT，同时保持相同的参数成本。部分实验结果如下图：

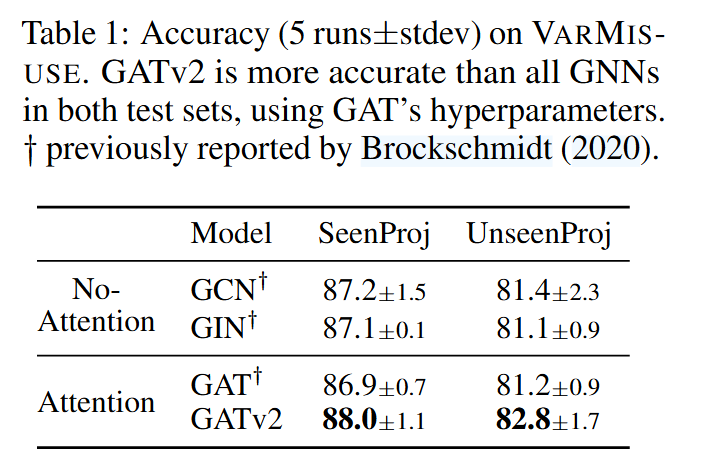
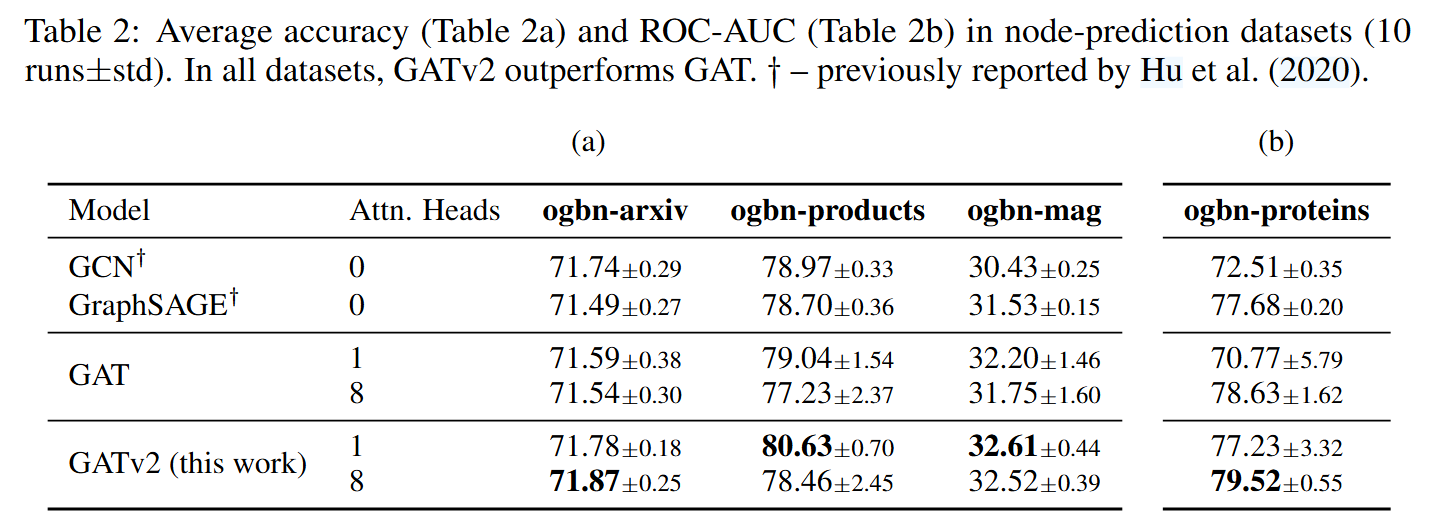
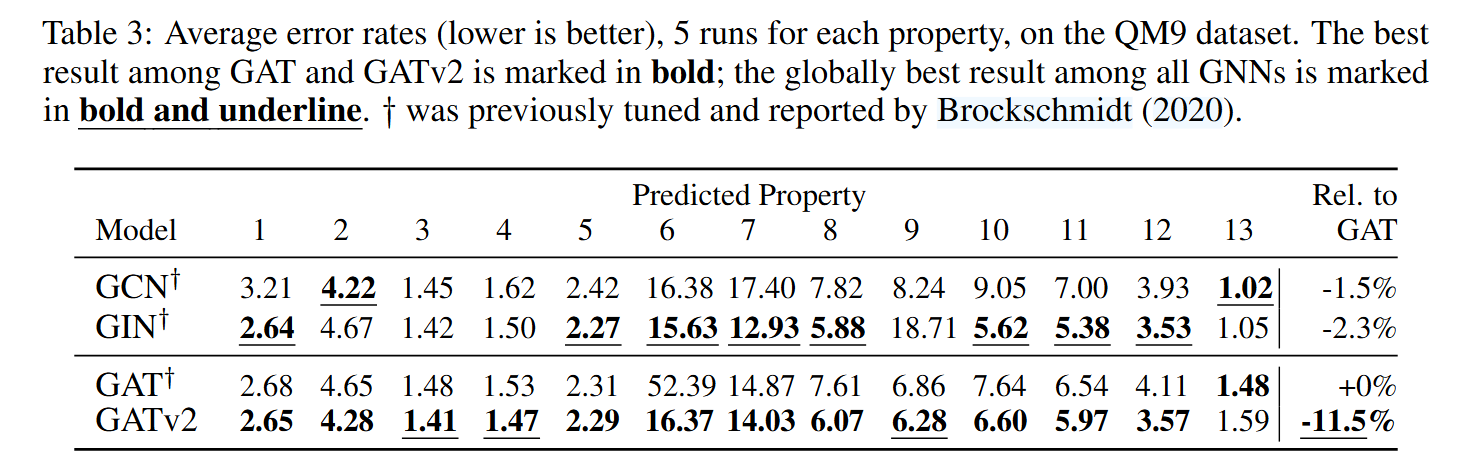
5、结论

本文确定了广泛使用的GAT并未计算动态注意力。相反，标准定义和实现中的注意力机制仅为静态：对于任何查询，其邻居评分在节点层面是单调递增的。此外，注意力系数的排序对于图中所有节点都是相同的，并且不依赖于查询节点。

为了解决这一局限性，我们提出了一种简单的修正并引入了GATv2：通过修改GAT中的操作顺序，GATv2实现了一个通用逼近器注意力函数，因此其表达能力严格优于GAT。