HDU 3516 Tree Construction 区间DP+四边形不等式优化

Tree Construction HDU - 3516
在第一象限上有 $n$ 个点，对于 $i<j$，有 $x_j>x_i,y_j<y_i$，将这些点用树连接起来，树的枝干只能向右或者向上走，问连接边的最小长度是多少？

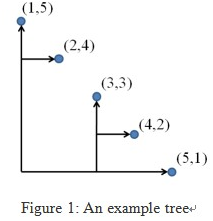
令 $dp[i][j]$ 为区间 $[i,j]$ 中的点形成的最小边长，则存在递推关系：

$dp[i][j]=\min\{dp[i][k]+dp[k+1][j]+x[k+1]-x[i]+y[k]-y[j]\}$

然后就可以用区间DP写出来啦，但是 $n\le 1000$ ，因此要考虑优化。采用四边形不等式优化。

可以观察到 $w(i,j)=x[k+1]-x[i]+y[k]-y[j]$ ，首先证明 $w(i,j)$ 为凸，即对于 $i<i+1\le j<j+1$：

$\begin{aligned} w(i,j)+w(i+1,j+1)&\le w(i,j+1)+w(i+1,j)\\ \tag{1} w(i,j)-w(i,j+1)&\le w(i+1,j)-w(i+1,j+1) \end{aligned}$

而 $w(i,j)-w(i,j+1)=y[j+1]-y[j]$ 跟 $i$ 无关，即两边相等，故凸性自然成立。

再证 $dp[i][j]$ 为凸，采用数学归纳法，参考 oi-wiki ，对于 $i<i+1\le j< j+1$ ，即证：

$dp[i][j]+dp[i+1][j+1]\le dp[i][j+1]+dp[i+1][j]$

首先设 $dp[i][j+1],dp[i+1][j]$ 的最优解分别在 $k_1,k_2$ 取到，并假设 $k_1< k_2$，则有 $i\le k_1<j,i+1\le k_2<j+1$，则有：

$\begin{aligned}\tag{2} dp[i][j]&\le dp[i][k_1]+dp[k_1+1][j]+w(i,j)\\ dp[i+1][j+1]&\le dp[i+1][k_2]+dp[k_2+1][j+1]+w(i+1,j+1) \end{aligned}$

由 $k_1+1<k_2+1\le j<j+1$，再根据归纳假设（dp 为凸），则有：

$dp[k_1+1][j]+dp[k_2+1][j+1]\le dp[k_1+1][j+1]+dp[k_2+1][j]\tag{3}$

将 $(2)$ 中两个不等式左右相加，得：

$dp[i][j]+dp[i+1][j+1]\le \\ dp[i][k_1]+dp[i+1][k_2]+dp[k_1+1][j]+dp[k_2+1][j+1]+w(i,j)+w(i+1,j+1)$

再根据 $(1)$ 中 $w$ 的凸性，以及不等式 $(3)$ ，可得：

$dp[i][j]+dp[i+1][j+1]\le \\ dp[i][k_1]+dp[i+1][k_2]+dp[k_1+1][j+1]+dp[k_2+1][j]+w(i,j+1)+w(i+1,j)\\ =dp[i][j+1]+dp[i+1][j]$

证毕。$k_1\ge k_2$ 时同理可证。

最后证明决策单调，参考 oi-wiki，令 $s[i][j]$ 表示 $dp[i][j]$ 的最优决策点，证明决策单调即证明 $s[i][j-1]\le s[i][j]\le s[i+1][j]$ ，首先证明前半部分。

令 $s[i][j-1]=k,s[i][j]=u$，用反证法，假如 $k>u$，则有 $u+1<k+1\le j-1<j$，根据已经证明了的 $dp$ 的凸性，有：

$dp[u+1][j-1]+dp[k+1][j]\le dp[u+1][j]+dp[k+1][j-1]$

又因为 $k$ 为 $dp[i][j-1]$ 的最优解，因此：

$dp[i][k]+dp[k+1][j-1]\le dp[i][u]+dp[u+1][j-1]$

以上两不等式左右相加，即有：

$dp[i][k]+dp[k+1][[j]\le dp[i][u]+dp[u+1][j]$

得到结论：对于 $dp[i][j]$ ，$k$ 比 $u$ 优，矛盾！因此 $k\le u$，即 $s[i][j-1]\le s[i][j]$ 。后半部分同理可证。

实际使用的时候其实只要看 $w(i,j)$ 满足区间包含单调性以及凸性，后面的 $dp$ 为凸以及决策单调性便都是成立的，可以直接使用（UPD：满足形如 $dp[i][j]=\min\{dp[i][k]+dp[k+1][j]+w(i,j)\}$，证明一下单调性以及凸性即可，但是会发现有些题目的转移方程并不一定这么整齐，比如P4767 [IOI2000]邮局，需要提供更加完整的证明，但是图快的话会把 s[i][j] 打个表，看看是否符合决策单调，如果符合，那就直接使用），这里证明一下是为了深入理解一下这么做为什么是对的。

实际实现时，设置数组 s[MAXN][MAXN] ，s[i][j] 表示 dp[i][j] 的最优决策值，初始化时令 s[i][i]=i （意思是区间 $[i,i]$ 的最优决策点为 $i$ ，因为只有这一个元素可以选择），然后在之前区间DP 最内层循环 k 的时候，把上下界限改为 s[i][j-1] 和 s[i+1][j] ，并在取最优 k 时及时更新 s[i][j] 就可以了。

代码如下：

#include<iostream>
#include<algorithm>
#include<cstring>
//#define WINE
#define MAXN 1010
#define INF 0x3f3f3f3f
using namespace std;
int n,x[MAXN],y[MAXN],dp[MAXN][MAXN];
int s[MAXN][MAXN];
int main(){
#ifdef WINE
    freopen("data.in","r",stdin);
#endif
    while(scanf("%d",&n)!=EOF){
        for(int i=1;i<=n;i++){
            scanf("%d%d",&x[i],&y[i]);
            s[i][i]=i;
        }
        memset(dp,0,sizeof(dp));
        for(int len=2;len<=n;len++)
            for(int i=1;i+len-1<=n;i++){
                int j=i+len-1;dp[i][j]=INF;
                for(int k=s[i][j-1];k<=s[i+1][j]&&k<j;k++)
                    if(dp[i][k]+dp[k+1][j]+x[k+1]-x[i]+y[k]-y[j]<dp[i][j]){
                        s[i][j]=k;
                        dp[i][j]=dp[i][k]+dp[k+1][j]+x[k+1]-x[i]+y[k]-y[j];
                    }
            }
        printf("%d\n",dp[1][n]);
    }
    return 0;
}