应用信息论基础第五章信道编码笔记

学习要点：

信道编码分析

联合典型序列
信道编码定理
信源信道联合编码定理

信道编码设计

经验主义设计
编码错误概率
典型信道编码

文章目录

5.1 基本概念
5.2 典型设计
5.3 信道编码定理

证明正定理
证明逆定理

5.4 典型信道编码
5.5 信源信道联合编码定理

5.1 基本概念

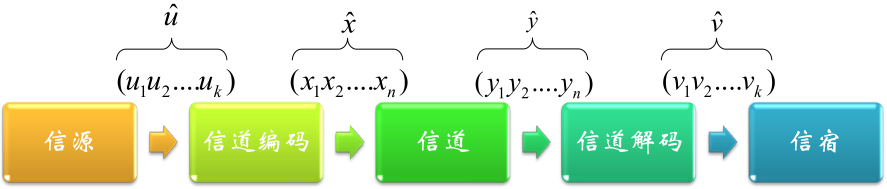
在这里插入图片描述

从通信角度看信道编码：
- 信道不可靠
- $\hat{W}$ 与传输的消息 $W$ 不同
研究目标：
- 使信息经信道传输后出现的差错最小！
信道构成 $\{\mathcal{X},q(y|x),\mathcal{Y}\}$
- 输入：符号集合 $\{1,2,...,M\}$
- 编码函数： $X^n:\{1,2,...,M\}\to\mathcal{X}^n$
- 译码函数： $g:\mathcal{Y}^n\to\{1,2,...,M\}$
信道编码 $(M,n)$ 码

信道编码：

原理：
- 增加冗余位，扩大信号空间，增大信号间距离
分类：
比如线性码（linear code）
- 编码函数为线性函数
- 任意个码字的线性组合仍然是码字

性能指标——错误概率：

条件错误概率：

$\begin{aligned} \lambda_i&=\mathrm{Pr}\{g(Y^n)\not=i|X^n=x^n(i)\}\\ &=\sum_{y^n}q(y^n|x^n(i))I(g(y^n)\not=i) \end{aligned}$

其中 $I(\cdot)$ 为指示函数

最大错误概率：

$\lambda^{(n)}=\max_{i\in\{1,...,M\}}\lambda_i$

算术平均错误概率：

$P_e^{(n)}=\frac{1}{M}\sum_{i=1}^M\lambda_i$

若输入等概，则算术平均错误概率等于译码错误概率
算术平均错误概率 $\le$ 最大错误概率

性能指标——码率：

码率： $R=\dfrac{\log_{|\mathcal{X}|}M}{n}$
- 表示的是每个码字母所能携带的最大信息量，其中 $\log_{|\mathcal{X}|}M$ 是一个发送的消息可能具有的最大熵， $n$ 为信道编码的长度，除以 $n$ 表示信道码中每个码字所能携带的最大信息量（从原理上讲 $R<1$ ），对应的单位是 bits/传输。（每一传输实际上就是发送一个信道码的一位，因为对于一个消息来说其信道码有 $n$ 位，所以需要 $n$ 次传输）
可达：
- 若存在（二元）序列 $(\lceil2^{nR}\rceil,n)$ 满足： $n\to\infty$ 时， $\lambda^{(n)}\to 0$ ，则称码率 $R$ 是可达的（achievable）
  - $2^{nR}\le\lceil2^{nR}\rceil<2^{nR}+1$
  - $(\lceil 2^{nR}\rceil,n)$ 简记为 $(2^{nR},n)$

信道容量的定义：

离散无记忆信道（DMC）的信道容量为所有可达码率的上确界（上确界指的是最小上界）， $C=\sup{R}$
- 小于信道容量的码率可以获得任意小的差错概率
- 蕴含着渐进无差错和码的存在性，指导工程实践
- 信道容量定义： $C=\max I(X;Y)$ ，相对容易求解，但无法保证信道无差错传输
- 香农第二定理说明了上述两种定义等价
  $C=\sup{R}\iff C=\max I(X;Y)$

5.2 典型设计

信道传输中如何减少差错？
香农公式： $C=W\log{(1+\dfrac{P_s}{N_0W})}$
提高抗干扰能力的方法：
- 增加功率（提高信噪比）
- 加大带宽（信号变化剧烈）
- 延长时间（降低速率）
最直观的设计：重复和增加冗余

重复码：
在这里插入图片描述

二进制信道编码的码率-误差分析：

在这里插入图片描述

码率 $R=\dfrac{k}{n}$
误码率 $P_e=\frac{1}{k}\sum_{i=1}^kP_e^i,P_e^i=\{v_i\not=u_i\},i=1,...,k$
码率 $R$ 和误码率 $P_e$ 在二进制独立信源以及二进制独立信道下的关系：

$R\le\frac{1-H(p)}{1-H(P_e)}$

证明：

Fano 不等式（二进制）
$H(X|Y)\le H(P_e)+P_e\log(K-1)=H(P_e)$
互信息
$\begin{aligned} I(X;Y)&\ge I(U,V)\ge\sum_{i=1}^kI(U_i;V_i)\\ &=\sum_{i=1}^k(H(U_i)-H(U_i|V_i))=k-\sum_{i=1}^kH(U_i|V_i)\\ &\ge k-kH(P_e) \end{aligned}$

$nC\ge k(1-H(P_e))\implies\frac{k}{n}\le\frac{1-H(p)}{1-H(P_e)}$

在这里插入图片描述
无差错传输的要求：

传输速率与信道容量 $R\le\dfrac{1-H(p)}{1-H(P_e)}=\dfrac{C}{1-H(P_e)}$
误码率 $P_e\ge H^{-1}(1-\dfrac{C}{R})$
若 $R>C$ ，则 $P_e>0$ ，传输有差错，通信不可靠
若 $R<C$ 或 $R=C$ ， $P_e$ 可以等于零

好码的要求：

相同误码率下，码率越高越好
$P_e=0$ ， $R$ 能无限提高吗？（信道编码定理想要回答的问题）

5.3 信道编码定理

典型序列（Typical Sequence）

渐进均分性定理（AEP）
- 若 $X_1,...X_n\sim p(x),i.i.d.,EX_n=\mu<\infty$ ，则
  $\frac{1}{n}\log{p(X_1,...,X_n)}\overset{\text{依概率}}{\longrightarrow} H(X)$
典型序列及典型集（typical set）
- 序列 $(x_1,...,x_n)\in\mathcal{X}^n$ 满足 $2^{-n(H(X)+\epsilon)}\le p(x_1,...,x_n)\le 2^{-n(H(X)-\epsilon)}$ ，典型序列的集合称为典型集 $A_\epsilon^{(n)}$
性质：
- 典型集的概率近似为 1
- 典型集中所有元素几乎是等概的
- 典型集的元素个数几乎等于 $2^{nH(X)}$

联合典型序列（Jointly Typical Sequence, JTS）

联合典型序列
- $(X,Y)\sim p(x,y)$ ，随机序列对 $(x^n,y^n)\in\mathcal{X}^n\times\mathcal{Y}^n$ 且
  - $|-\frac{1}{n}\log{p(x^n)}-H(X)|<\epsilon$
  - $|-\frac{1}{n}\log{p(y^n)}-H(Y)|<\epsilon$
  - $|-\frac{1}{n}\log{p(x^n,y^n)-H(X,Y)}|<\epsilon$
  - 其中 $p(x^n,y^n)=\prod_{i=1}^np(x_i,y_i)$
联合典型集
- 联合典型序列构成的集合记为 $A_\epsilon^{(n)}$

联合渐进均分性（Joint AEP）

$(X^n,Y^n)\sim p(x^n,y^n)=\prod_{i=1}^np(x_i,y_i),i.i.d.$
- 当 $n\to\infty$ 时， $\mathrm{Pr}\{(X^n,Y^n)\in A_\epsilon^{(n)}\}\to 1$
- $|A_\epsilon^{(n)}|\le 2^{n(H(X,Y)+\epsilon)},|A_\epsilon^{(n)}|\ge(1-\epsilon)2^{n(H(X,Y)-\epsilon)}$
- 如果 $\tilde{X}^n$ 与 $\tilde{Y}^n$ 独立且 $(\tilde{X}^n,\tilde{Y}^n)\sim p(x^n)p(y^n)$ ，则 $\mathrm{Pr}\{(\tilde{X}^n,\tilde{Y}^n)\in A_\epsilon^{(n)}\}\le 2^{-n(I(X;Y)-3\epsilon)}$ ，且对于充分大的 $n$ ，有 $\mathrm{Pr}\{(\tilde{X}^n,\tilde{Y}^n)\in A_\epsilon^{(n)}\}\ge(1-\epsilon)2^{-n(I(X;Y)+3\epsilon)}$

在这里插入图片描述
信道编码定理（Channel Coding Theorem, CCT）

信息论最重要的结论
- Shannon Theorem II (Noisy-channel coding theorem)
- 有噪信道可实现几乎无失真传输
该定理的结果与直观感觉正好相反
- 若信道有错误，如何能够完全纠正？
- 尤其是：纠正的过程本身也受错误的影响
基本思想：
- 允许任意小的非零错误概率存在
- 构造码列 $C^{(n)},n\to\infty$ ，保证大数定律或 AEP 生效
- 计算随机码的平均错误概率，随机码=所有码的平均=存在至少一个满足要求的码，即由于随机码

表述：

正定理：对于离散无记忆信道（DMC），小于其容量 $C$ 的所有码率是可达的，即对于任意 $R<C$ ，可以找到一个信道编码方案 $(2^{nR},n)$ ，使得最大错误概率 $\lambda^{(n)}\to0$

逆定理：对于任意编码方案 $(2^{nR},n)$ ，若 $\lambda^{(n)}\to0$ ，则必有 $R\le C$

证明正定理

已知：DMC, $\mathcal{X},\mathcal{Y},p(y|x),X\sim p(x)$

编码：

设 $p(x)$ 达到信道容量 $C$ ，即 $I(X;Y)=C$ ，对于充分大的 $n$ ，根据 $p(x)$ 独立生成 $(2^{nR},n)$ 码 $C^{(n)}$
- $\forall x^n\in C^{(n)},p(x^n)=\prod_{i=1}^np(x_i)$ ， $C^{(n)}$ 有 $2^{nR}$ 个码字
- 设接收向量为 $y^n$ ，则 $p(y^n|x^n)=\prod_{i=1}^np(y_i|x_i)$

译码（前两种最优，第三种简单）：

最大后验概率（MAP）：选择 $\hat{x}^n\in C^{(n)}$ 满足 $p(\hat{x}^n|y^n)$ 最大。
最大似然（ML）：选择 $\hat{x}^n\in C^{(n)}$ 满足 $p(y^n|\hat{x}^n)$ 最大。
典型集译码：选择 $\hat{x}^n\in C^{(n)}$ 满足 $\hat{x}^n$ 与 $y^n$ 联合典型。
若接收到的序列 $y^n$ 存在唯一的发送序列 $\hat{x}^n$ 与其具有联合典型性，则解码成功；
否则，解码错误，记为事件 $\mathcal{E}$
目标：将证明若 $R<C$ ，则 $\mathrm{Pr}\{\mathcal{E}\}\to0$
- 若平均错误概率 $\to0$ ，则 $\lambda^{(n)}\to0$ ，从而 $R$ 可达。

错误事件（两种情形）：

存在 $\hat{x}^n$ 与 $y^n$ 联合典型， $x^n$ 与 $y^n$ 联合典型，但 $\hat{x}^n \neq x^n$
$x^n$ 和 $y^n$ 非联合典型

错误概率：

记 $x^n(i)$ 为第 $i$ 个码字， $i=1,...,M,M=2^{nR}$ ，假设发送 $x^n(1)$
令 $E_i\triangleq\{(x^n(i),y^n)\in A_\epsilon^{(n)}\}$
则
$\begin{aligned} \lambda_1&=\mathrm{Pr}\{\mathcal{E}|x^n(1)\}=\mathrm{Pr}\{\bar{E}_1\cup E_2\cup...\cup E_M\}\\ &\le \mathrm{Pr}\{\bar{E}_1\}+\sum_{i=2}^M\mathrm{Pr}\{E_i\}\\ &\le\epsilon+(M-1)2^{-n[I(X;Y)-3\epsilon]}\\ &\le\epsilon+2^{3n\epsilon}\cdot 2^{-n(C-R)} \\ &\le 2\epsilon \end{aligned}$
由对称性 $\lambda_i=\lambda_1\le2\epsilon\implies P_e^{(n)}=\mathrm{Pr}\{\mathcal{E}\}\le2\epsilon$

码率的可达性

$C^{(n)}$ 是按照 $p(x)$ 随机生成的 $(M,n)$ 码，译码错误概率记为 $P_e^{(n)}$
$C^{(n)}$ 为所有服从 $p(x)$ 的 $(M,n)$ 码的平均
- $\exists$ 最优的 $(M,n)$ 码 $C^{(n)*}$ ，使得 $\mathrm{Pr}\{C^{(n)}出错\}\le2\epsilon$
- 不妨设 $\lambda_1^*\le\lambda_2^*\le...\le\lambda_M^*$ ，则 $\lambda_{M/2}^*\le4\epsilon$
构造新码 $\tilde{C}^{(n)*}=\{C^{(n)*}错误概率最小的一半码字\}$
- 最大错误概率 $\tilde{\lambda}^{(n)*}\le4\epsilon$
- $\tilde{C}^{(n)*}$ 有 $\frac{M}{2}=2^{nR-1}$ 个码字，码率为 $R(1-\frac{1}{n})$
- 当 $n\to\infty$ 时， $\tilde{C}^{(n)*}$ 满足 $R(1-\frac{1}{n})\to R$ 且 $\tilde{\lambda}^{(n)*}\to0$
- 因此 $R$ 可达