应用信息论基础 第四章 信道与信道容量 笔记

学习要点：

• 信道特性

1. 基本概念
2. 信道模型及分类
3. 信道容量特性

• 信道容量计算

4. 离散信道容量
5. 组合信道容量
6. 连续及模拟信道容量

文章目录

• 4.1 信道与信道容量
• 4.2 离散信道的信道容量
• 4.3 信源与信道的匹配
• 4.4 组合的信道
• 4.5 连续信道的信道容量
• 4.6 模拟信道的信道容量

4.1 信道与信道容量

无记忆信道指的信道转移的这个特性在每一时刻彼此是独立的。






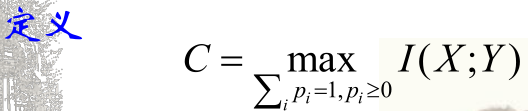
符号变为 $m$ 个的话，$C=\max I(X;Y)=\max H(X)=\log{m}$ bit

无噪声应该不等于无差错，因为假如两个不同的输入都以概率 $1$ 映射到了同一个输出，那么也是产生了差错的。

这个例子很有意思。可以找到明确的译码方案来达到这个容量。

4.2 离散信道的信道容量

离散无记忆信道（DMC，discrete memoryless channel）

无记忆性：若某一时刻的输出仅和当时的输入有关，而与过去的输入和输出无关。

对于转移概率矩阵 $Q$ ，它的每一行的和都是 $1$ ，但是列和不一定是 $1$





其中 $J$ 是输出字符集的大小，$K$ 是输入字符集的大小。

额，这个证明我觉得可有可无，因为对称信道每一行是不同的排列，对于不同的输入字符，其输出的概率分布里的数值形成的集合是相同的，因此每一行的熵都相同，自然有 $H(Y|X)=H(Y|a_k)$，其中 $a_k$ 为第 $k$ 个输入字符。

然后 $C$ 在输出分布为均匀分布时取得。

这个定理也很显然，对于对称信道，输出等概时，输入也是等概。我觉得这个证明写复杂了，对称信道每一行是不同的排列，每一列也是不同的排列，因此每一行的和是相同的，并且每一列的和也是相同的，也易知行和与列和都是 $1$，因此在输入等概时可以直接得出 $H_0=\dfrac{1}{J}$

其中 $K$ 表示输入输出字符集大小，强对称信道中输入输出字符集的大小是一样的。

现在就是通过调整输入分布，来得到最大的 $I(X;Y)$ ，也就是 $I(p,Q)$，从而得到信道容量。其中 $p$ 是输入分布，$Q$ 是转移概率矩阵。

这个可以稍微算一下：

$\begin{aligned} I(X=0;Y)&=H(Y)-H(Y|X=0)\\ &=-2\times\frac{3}{8}\log{\frac{3}{8}}-\frac{1}{4}\log\frac{1}{4}-(-\frac{3}{4}\log\frac{3}{4}-\frac{1}{4}\log\frac{1}{4})\\ &=\frac{3}{4} \end{aligned}$

剩下的不算了，道理一样的。

这个定理的意思是，假如我们现在找到了一个能够达到信道容量的最佳分布 $p^*$，那么对于概率不为 $0$ 的输入字符，其与输出字符的互信息必等于信道容量；假如该输入字符概率为 $0$ ，那么互信息必小于等于信道容量。

互信息的公式要记一下：

$\begin{aligned} I(X;Y)&=\sum_k\sum_jp(a_k,b_j)\log\frac{p(a_k,b_j)}{p(a_k)p(b_j)}\\ &=\sum_k\sum_jp(a_k)q(b_j|a_k)\log\frac{p(a_k)q(b_j|a_k)}{p(a_k)p(b_j)}\\ &=\sum_k\sum_jp(a_k)q(b_j|a_k)\log\frac{q(b_j|a_k)}{p(b_j)}\\ &=\sum_kp(a_k)\sum_jq(b_j|a_k)\log\frac{q(b_j|a_k)}{p(b_j)}\\ &=\sum_kp(a_k)I(X=a_k;Y)\\ I(X=a_k;Y)&=\sum_jq(b_j|a_k)\log\frac{q(b_j|a_k)}{p(b_j)}\\ \end{aligned}$

额，这个求偏导的地方步骤写的很简略…

$\begin{aligned} \frac{\partial g(p)}{\partial p(a_k)}&=\frac{\partial}{\partial p(a_k)}[\sum_{i=1}^Kp(a_i)\sum_{j=1}^Jq(b_j|a_i)\log\frac{q(b_j|a_i)}{p(b_j)}]-\mu\\ &=\frac{\partial}{\partial p(a_k)}[\sum_{i=1}^Kp(a_i)\sum_{j=1}^Jq(b_j|a_i)\log\frac{q(b_j|a_i)}{\sum_{i=1}^Kp(a_i)q(b_j|a_i)}]-\mu\\ &=\sum_{j=1}^Jq(b_j|a_k)\log\frac{q(b_j|a_k)}{p(b_j)}+\sum_{i=1}^Kp(a_k)\sum_{j=1}^Jq(b_j|a_k)\frac{\partial}{\partial p(a_k)}\log\frac{q(b_j|a_k)}{\sum_{i=1}^Kp(a_i)q(b_j|a_i)}-\mu\\ &=\sum_{j=1}^Jq(b_j|a_k)\log\frac{q(b_j|a_k)}{p(b_j)}-\sum_{i=1}^Kp(a_k)\sum_{j=1}^Jq(b_j|a_k)\frac{q(b_j|a_k)}{\sum_{i=1}^Kp(a_i)q(b_j|a_i)}\log{e}-\mu\\ &=\sum_{j=1}^Jq(b_j|a_k)\log\frac{q(b_j|a_k)}{p(b_j)}-\sum_{j=1}^Jp(b_j)\frac{q(b_j|a_k)}{p(b_j)}\log{e}-\mu\\ &=\sum_{j=1}^Jq(b_j|a_k)\log\frac{q(b_j|a_k)}{p(b_j)}-\sum_{j=1}^Jq(b_j|a_k)\log{e}-\mu\\ &=I(X=a_k;Y)|_{p=p^*}-\log{e}-\mu \end{aligned}$

重点就是分母上的 $p(b_j)$ 在求导的时候要展开。

妙啊。

单调递减这个也很显然，把分母写开之后发现 $p(a_k)$ 在分母这里，一层层推出去就发现这玩意是单减的。

二元对称信道怎么搞都行，可以直接 $C=\max{I(X;Y)=\max{H(Y)}-H(Y|X)}=\max{H(Y)}-H(\epsilon)=1-H(\epsilon)$

等号在输出字符之间独立时取到（因为信道是无记忆的，所以输出字符独立要求输入字符独立）

有记忆信道的结论和无记忆信道的结论中的不等号的方向是相反的。

4.3 信源与信道的匹配

为啥这么复杂。。要我来的话：$I(X;Y)$ 关于 $p(y)$ 上凸，因此极值点唯一。

4.4 组合的信道

这个和信道很有意思

4.5 连续信道的信道容量

4.6 模拟信道的信道容量