Convex Optimization: 3 Convex functions 作业

3.1, 3.2, 3.22, 3.28, 3.39, A2.23, A2.42, A2.46.

文章目录

• 3.1
• 3.2
• 3.22
• 3.28
• 3.39
• A2.23

3.1

这道题考的是凸函数的定义。假设一个函数 $f:\mathbf{R}\to\mathbf{R}$ ，并且 $a,b\in\mathbf{dom}\ f$ 且 $a<b$ 。

（a）证明对于所有的 $x\in[a,b]$ 都有：

$f(x)\le\frac{b-x}{b-a}f(a)+\frac{x-a}{b-a}f(b)$

证明：显然 由凸函数的定义，存在 $\theta\in[0,1]$ 使得

$f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y)$

令 $y=x,\theta=\dfrac{b-x}{b-a}$，则有：

$f(x)\le\frac{b-x}{b-a}f(a)+\frac{x-a}{b-a}f(b)$

（b）证明对于所有的 $x\in(a,b)$ ，有：

$\frac{f(x)-f(a)}{x-a}\le\frac{f(b)-f(a)}{b-a}\le\frac{f(b)-f(x)}{b-x}$

如图：

这个说的就是 ab 的斜率要大于 ax 之间的斜率，小于 xb 之间的斜率。

（c）假设 $f$ 可微，用 （b） 中的结果证明：

$f'(a)\le\frac{f(b)-f(a)}{b-a}\le f'(b)$

证明：对 （b） 的结果，左边令 $x\to a$，右边令 $x\to b$ ，即可得 （c）

（d）假设 $f$ 二阶可微，用 （c） 中的结果证明 $f''(a)\ge0$ 并且 $f''(b)\ge0$ 。

证明：由 （c）可得：

$\frac{f'(b)-f'(a)}{b-a}\ge0$

取极限 $b\to a$ 可得 $f''(a)\ge0$ ，同理可得 $f''(b)\ge0$

3.2

对于第一个图来说，这个可以是 quasiconvex 的，因为根据定义，其 sublevel sets:

$S_\alpha=\{x\in\mathbf{dom}\ f|f(x)\le\alpha\}$

是凸的（你在这个涂横着来一刀，这个面下面和这个函数形成了一个凸集），同理，这个肯定不是 concave 或 quasiconcave ，因为其上面的集合不是凸的；

这个不是凸的，因为沿下图的路径 I 得到的曲线看出来其不是凸的：

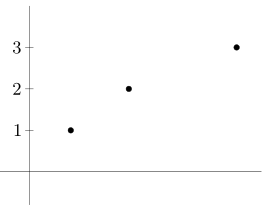
第二个图可能是凹的，也可能是 quasiconcave，但不能是凸的或 quasiconvex 因为其 sublevel sets 不是凸的。

3.22

证明以下函数是凸函数：

（a）$f(x)=-\log(-\log(\sum_{i=1}^me^{a_i^Tx+b_i}))$ ，定义域为 $\{x|\sum_{i=1}^me^{a_i^T+b_i<1}\}$ ，可以直接使用结论：$\log(\sum_{i=1}^ne^{y_i})$ 是凸的（注：log-sum-exp 的凸性是通过二阶导证的）。

首先复习一下 composition rules，对于函数 $f(x)=h(g(x))$ 来说，满足以下两个条件之一，$f$ 就是凸的：

1. $g$ 是凸的，$h$ 是凸的，并且 $\tilde{h}$ 不减
2. $g$ 是凹的，$h$ 是凸的，并且 $\tilde{h}$ 不增

这个怎么记呢？可以这样记：外面函数 $h$ 总要求是凸的，里面 $g$ 则不同，那么如何记忆 $g$ 的凹凸与增减之间的对应的，脑补 $f''(x)$ 的形式，里面会有一项 $h'g''$ ，若 $g$ 凸，则 $g''\ge0$，故要求 $h'\ge0$ ，即 $h$ 不减；若 $g$ 凹，则 $g''\le0$ ，故要求 $h'\le0$，即 $h$ 不增。

（证明方法是对 $f$ 求二阶导，然后应用链式法则得到 $g,h$ 的相关一二阶导数的要求）（如下）

所以对于这道题，令 $g(x)=-\log(\sum_{i=1}^me^{a_i^Tx+b_i})$ 则这玩意儿是凹的，所以我们来看上面说的第二个条件。又知 $h(x)=-\log(x)$ 是凸的，并且不增，因此也满足第二个条件，所以 $f$ 是凸的。 Done.

（b） $f(x,u,v)=-\sqrt{uv-x^Tx}$ ，定义域为 $\{(x,u,v)|uv>x^Tx,u,v>0\}$ ，可以使用结论：$x^Tx/u$ 在 $(x,u),u>0$ 上是凸的，$-\sqrt{x_1x_2}$ 在 $\mathbf{R}_{++}^2$ 上是凸的。

$\begin{aligned} f(x,u,v)&=-\sqrt{uv-x^Tx}\\ &=-\sqrt{u(v-\frac{x^Tx}{u})} \end{aligned}$

外部函数 $h(x_1,x_2)=-\sqrt{x_1x_2}$ 为凸且单调递减，内部函数 $g_1(u,v,x)=u$ 以及 $g_2(u,v,x)=v-x^Tx/u$ 都是凹函数，因此 $f(u,v,x)=h(g(u,v,x))$ 为凸。

（c）$f(x,u,v)=-\log(uv-x^Tx)$ ，定义域为 $\{(x,u,v)|uv>x^Tx,u,v>0\}$

$f(x,u,v)=-\log{u}-\log(v-x^Tx/u)$

第一项是凸的，第二项内部 $v-x^Tx/u$ 是凹的，因为 $v$ 是线性的，$x^Tx/u$ 在 $\{(x,u)|u>0\}$ 上是凸的，又因为外部函数 $-\log{t}$ 凸且单调减，因此第二部分凸。

（d）$f(x,t)=-(t^p-\|x\|_p^p)^{1/p}$ ，其中 $p>1$ ，并且定义域为 $\{(x,t)|t\ge\|x\|_p\}$ ，可以使用的结论有：$\|x\|_p^p/u^{p-1}$ 在 $(x,u),u>0$ 是凸的（证明见练习3.23），并且 $-x^{1/p}y^{1-1/p}$ 在 $\mathbf{R}_+^2$ 上是凸的（证明见练习3.16）。

$\begin{aligned} f(x,t)&=-(t^{p-1}(t-\frac{\|x\|_p^p}{t^{p-1}}))^{1/p}\\ &=-t^{1-1/p}(t-\frac{\|x\|_p^p}{t^{p-1}})^{1/p}\\ \end{aligned}$

其中外部函数 $h(y_1,y_2)=-y_1^{1/p}y_2^{1-1/p}$ 是凸的并且单减，内部函数为：

$g_1(x,t)=t^{1-1/p},\quad g_2(x,t)=t-\frac{\|x\|_p^p}{t^{p-1}}$

这两个函数都是凹函数，因此总体为凸。

（e）$f(x,t)=-\log(t^p-\|x\|_p^p)$，其中 $p>1$ ，定义域为 $\{(x,t)|t>\|x\|_p\}$

$\begin{aligned} f(x,t)&=-\log{t^{p-1}}-\log(t-\|x\|_p^p/t^{p-1})\\ &=-(p-1)\log{t}-\log(t-\|x\|_p^p/t^{p-1}) \end{aligned}$

第一项是凸的，第二个内部是一个凹函数，外部是一个单减的凸函数，因此整体是凸。

3.28

考的是能够保持凸性的操作。

用仿射函数的 pointwise supremum 来表示一个凸函数。这个问题是对书上 83 页结论的扩展，不同的是此处 $\mathbf{dom}f\neq \mathbf{R}^n$，令 $f:\mathbf{R}^n\to\mathbf{R}^n$ 是一个凸函数，定义 $\tilde{f}:\mathbf{R}^n\to\mathbf{R}$ 为所有 $f$ 的全局 unerestimators 的仿射函数的 pointwise supremum：

$\tilde{f}(x)=\sup\{g(x)|g\text{ affine,}g(z)\le f(z)\text{ for all }z\}$

证明：

（a）证明对于 $x\in\mathbf{int\ dom\ }f$ ，有 $f(x)=\tilde{f}(x)$

令点 $(x,f(x))$ 在 $\mathbf{epi}\ f$ 的边界上（$\mathbf{epi}\ f$ 就是该函数上面的点集），（不选择 $\mathbf{int\ epi\ }f$ 是因为当这个点在 $\mathbf{int\ epi\ }f$ 上时，对于任意小的 $\epsilon>0$ 有 $(x,f(x)-\epsilon)\in\mathbf{epi\ }f$ ，这是不可能的，根据 2.5.2 节的结果，可知对于 $(x,f(x))$ 处的 $\mathbf{epi\ }f$ ，存在一个支持超平面，即 $a\in\mathbf{R}^n,b\in\mathbf{R}$ ，使得：

$a^Tz+bt\ge a^Tx+bf(x)\text{ for all } (z,t)\in \mathbf{epi\ }f$

如果 $(z,t)\in\mathbf{epi\ }f$ ，则 $t$ 可以任意大，因此我们得出结论 $b\ge0$ 。

假设 $b=0$ ，则：

$a^Tz\ge a^Tx\text{ for all }z\in\mathbf{dom\ }f$

和 $x\in\mathbf{int\ dom}\ f$ 相矛盾！因此 $b>0$ 。上述不等式同除以 $b$ 得到：

$t\ge f(x)+(a/b)^T(x-z)\text{ for all }(z,t)\in\mathbf{epi}\ f$

因此仿射函数：

$g(z)=f(x)+(a/b)^T(x-z)$

为 $f$ 的 affine global underestimator ，所以根据 $\tilde{f}$ 的定义：

$f(x)\ge\tilde{f}(x)\ge g(x)$

但是 $g(x)=f(x)$，因此必须有 $f(x)=\tilde{f}(x)$

（b）证明如果 $f$ 是闭，那么 $f=\tilde{f}$ （即 $\mathbf{epi\ }f$ 是一个闭集）

• A3.3 ：一个函数 $f:\mathbf{R}^n\to\mathbf{R}$ 是闭的，如果对 $\forall\alpha\in\mathbf{R}$ ，其 sublevel set

$\{x\in\mathbf{dom\ }f|f(x)\le\alpha\}$

是闭的。这等价于 $f$ 的 epigraph

$\mathbf{epi}\ f=\{(x,t)\in\mathbf{R}^{n+1}|x\in\mathbf{dom\ }f,f(x)\le t\}$

是闭的。

一个闭的凸集是所有包含这个集合半平面的交集（见第二章，例 2.20）。对 $\mathbf{epi\ }f$ 使用这个结论，定义：

$H=\{(a,b,c)\in\mathbf{R}^{n+2}|(a,b)\neq0,\inf_{(x,t)\in\mathbf{epi\ }f}(a^Tx+bt)\ge c\}$

粗略来说，$H$ 是包含 $\mathbf{epi\ }f$ 的所有半平面的集合，根据第二章的结论，

$\mathbf{epi\ }f=\bigcap_{(a,b,c)\in H}\{(x,t)|a^T+bt\ge c\}$

显然 $H$ 中所有元素都满足 $b\ge0$ ，实际上 $b>0$，因此仿射函数：

$h(x)=-(a/b)^Tx+c/b$

是 $\le f$ 的，因为对于 $\forall(x,t)\in\mathbf{epi}\ f$，有

$t\ge f(x)\ge-(a/b)^Tx+c/t=h(x)$

相反地，假如 $h(-a^Tx+c)\le f$ 则 $(a,1,c)\in H$ ，需要证明：

$\mathbf{epi\ }f=\bigcap_{(a,b,c)\in H,b>0}\{(x,t)|a^Tx+bt\ge c\}$

也就是说 $\mathbf{epi}\ f$ 是所有包含 $\mathbf{epi}\ f$ 的非垂直的半平面的交集。然后证明：

$\bigcap_{(a,b,c)\in H,b>0}\{(x,t)|a^Tx+bt\ge c\}=\bigcap_{(a,b,c)\in H}\{(x,t)|a^Tx+bt\ge c\} \tag{1}$

显然左边的包含右边的，现在证假如在左边，那么它一定在右边，用反证法，首先设 $(\bar{x},\bar{t})$ 在左边的集合中，即：

$a^T\bar{x}+b\bar{t}\ge c$

对于所有的半平面 $a^Tx+bt\ge c$ 并且不是垂直的（即 $b>0$）并且包含 $\mathbf{epi\ } f$ ，假设 $(\bar{x},\bar{t})$ 不在右边的集合中，即存在 $(\tilde{a},\tilde{b},\tilde{c})\in H$ （$\tilde{b}=0$ 也是必要的），使得：

$\tilde{a}^T\bar{x}<\tilde{c}$

$H$ 至少包含一个元素 $(a_0,b_0,c_0)$ 其中 $b_0>0$ （要不然 $\mathbf{epi\ }f$ 将会是垂直半平面们的交集了），考虑一个半平面为 $(\tilde{a},0,\tilde{c})+\epsilon(a_0,b_0,c_0)$ ，其中 $\epsilon>0$ ，这个半平面是非垂直的，并且对于 $\forall (x,t)\in \mathbf{epi\ }f$ ，它是包含 $\mathbf{epi\ }f$ 的：

$(\tilde{a}+\epsilon a_0)^Tx+\epsilon b_0 t\ge\tilde{a}^Tx+\epsilon(a_0^T+b_0t)\ge\tilde{c}+\epsilon c_0$

原因是 $\tilde{a}^Tx\ge\tilde{c}$ 和 $a_0^Tx+b_0t\ge c_0$ 都包含 $\mathbf{epi\ }f$ ，但是对于 $\epsilon>0$ ，有：

$(\tilde{a}+\epsilon a_0)^Tx+\epsilon b_0 t\ge\tilde{a}^Tx+\epsilon(a_0^T+b_0t)<\tilde{c}+\epsilon c_0$

因此半平面不包含 $(\bar{x},\bar{t})$ ，这和假设矛盾，因此 $(1)$ 是成立的。

3.39

共轭函数的性质。

（a）一个凸函数加上一个仿射函数的共轭：定义 $g(x)=f(x)+c^Tx+d$ ，其中 $f$ 是凸的，用 $f^*$ 来表示 $g^*$ ：

$\begin{aligned} g^*(y)&=\sup(y^Tx-f(x)-c^Tx-d)\\ &=\sup((y-c)^Tx-f(x))-d\\ &=f^*(y-c)-d \end{aligned}$

（b）透视函数的共轭：用 $f^*$ 来表示凸函数 $f$ 的透视函数：

$\begin{aligned} g^*(y,s)&=\sup_{x/t\in\mathbf{dom\ }f,t>0}(y^Tx+st-t(f(x/t)))\\ &=\sup_{t>0}\sup_{x/t\in\mathbf{dom\ }f}(t(y^T(x/t)+s-f(x/t)))\\ &=\sup_{t>0}t(s+\sup_{x/t\in\mathbf{dom\ }f}(y^T(x/t)-f(x/t)))\\ &=\sup_{t>0}t(s+f^*(y))\\ &=\begin{cases} 0&s+f^*(y)\le0\\ \infty&\text{otherwise.} \end{cases} \end{aligned}$

（c）共轭以及最小：令 $f(x,z)$ 为 $(x,z)$ 上的凸函数，定义 $g(x)=\inf_zf(x,z)$ ，用 $f^*$ 来表示 $g^*$：

$\begin{aligned} g^*(y)&=\sup_x(x^Ty-\inf_zf(x,z))\\ &=\sup_{x,z}(x^Ty-f(x,z))\\ &=f^*(y,0) \end{aligned}$

作为应用，用 $h^*,A,b$ 来表示函数 $g(x)=\inf_z\{h(z)|Az+b=x\}$ 的共轭，其中 $h$ 是凸的：

首先我们要找到 $f(x,z)$：

$f(x,z)=\begin{cases} h(z)&Az+b=x\\ \infty&\text{otherwise.} \end{cases}$

则有：

$\begin{aligned} f^*(y,v)&=\sup(y^Tx+v^Tz-f(x,z))\\ &=\sup_{Az+b=x}(y^Tx+v^Tz-h(z))\\ &=\sup_z(y^T(Az+b)+v^Tz-h(z))\\ &=b^Ty+\sup_z(y^TAz+v^Tz-h(z))\\ &=b^Ty+h^*(A^Ty+v) \end{aligned}$

我感觉应该是我上面的这种写法，不知道答案为啥这样写：

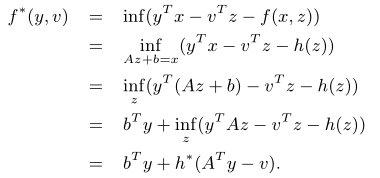
但是结果一样：

$g^*(y)=f^*(y,0)=b^Ty+h^*(A^Ty)$

（d）共轭的共轭：证明假如 $f$ 是凸的且闭的，那么 $f=f^{**}$ （一个函数其 epigraph 是闭的，则其是闭的），提示：证明 $f^{**}$ 是 $f$ 所有的 affine global underestimators 的点式上确界，然后用练习 3.28 的结论。

根据定义：

$f^*(y)=\sup_x(y^Tx-f(x))$

假如 $y\in\mathbf{dom\ }f^*$ ，则仿射函数 $h(x)=y^Tx-f^*(y)$ 小于等于 $f$ ，反之，假如 $h(x)=a^Tx+b$ 小于等于 $f$ ，则 $a\in\mathbf{dom\ }f^*$ 并且 $f^*(a)\le-b$ ，那么所有小于等于 $f$ 的仿射函数的集合正好就等于所以函数 $h(x)=y^Tx+c$ 的集合，其中：

$y\in\mathbf{dom\ }f^*,\quad c\le-f^*(y).$

因此，根据练习 3.28 ，有：

$f(x)=\sup_{y\in\mathbf{dom\ }f^*}(y^Tx-f^*(y))=f^{**}(y)$

A2.23

证明以下函数 $f:\mathbf{R}^n\to\mathbf{R}$ 是凸的：

（a）$f(x)=-\exp(-g(x))$ ，其中 $g:\mathbf{R}^n\to\mathbf{R}$ 定义域是凸的，并且满足：

$\begin{bmatrix} \nabla^2g(x)&\nabla g(x)\\ \nabla g(x)^T&1 \end{bmatrix} \succeq0$

其中 $x\in\mathbf{dom\ }g$ 。

求 $f$ 的梯度以及 Hessian：

$\begin{aligned} \nabla f(x)&=e^{-g(x)}\nabla g(x)\\ \nabla^2f(x)&=e^{-g(x)}\nabla^2g(x)-e^{-g(x)}\nabla g(x)\nabla g(x)^T\\ &=e^{-g(x)}(\nabla^2g(x)-\nabla g(x)\nabla g(x)^T)\\ &\succeq 0 \end{aligned}$

因此 $f$ 凸。

（b）函数：

$f(x)=\max\{\|APx-b\||P\text{ is a permutation matrix}\}$

其中 $A\in\mathbf{R}^{m\times n},b\in\mathbf{R}^m$ 。

因为 $f$ 是带有参数 $P$ 的 $\|APx-b\|$ 的最大值，又因为 $\|APx-b\|$ 是凸函数，因此 $f$ 凸。