树状数组
树状数组
树状数组是一种支持单点修改和区间查询的,代码量小 (这是重点) 的数据结构。
事实上,树状数组能解决的问题是线段树能解决的问题的子集:树状数组能做的,线段树一定能做;线段树能做的,树状数组不一定可以。然而,树状数组的代码要远比线段树短,时间效率常数也更小,因此仍有学习价值。
有时,在差分数组和辅助数组的帮助下,树状数组还可解决更强的 区间加单点值 和 区间加区间和 问题。
树状数组工作原理
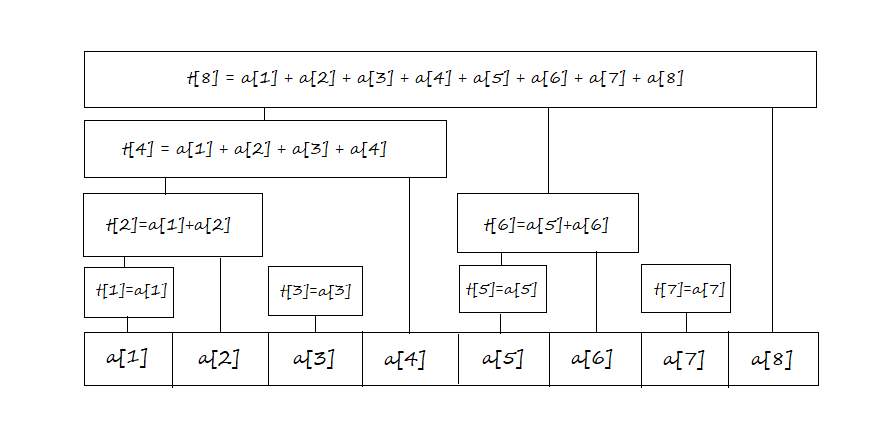
\(t[x]\) 管辖一段左边界是 \(x-lowbit(x)+1\)、右边界是 \(x\) 的区间总信息(如图)
基本操作
\(lowbit\)
将 \(x\) 的二进制所有位全部取反,再加 \(1\),就可以得到 \(-x\) 的二进制编码
设原先 \(x\) 的二进制编码是 \((...)10...00\),全部取反后得到 \([...]01...11\), 加 \(1\) 后得到 \([...]10...00\),也就是 \(-x\) 的二进制编码了。这里 \(x\) 二进制表示中第一个 \(1\) 是 \(x\) 最低位的 \(1\)
\((...)\) 和 \([...]\) 中省略号的每一位分别相反,所以 \(x \& -x = (...)10...00 \& [...]10...00 = 10...00\),得到的结果就是 \(lowbit\)
il int lowbit(cs int x){
return x&(-x);
}
\(update\)
对于修改 \(x\),只需要修改 \(x\) 会影响的 \(\log x\) 个 \(t_i\) 即可
il void update(int x,cs int k){
while(x<=r) tr[x]+=k,x=lowbit(x);
}
\(query\)
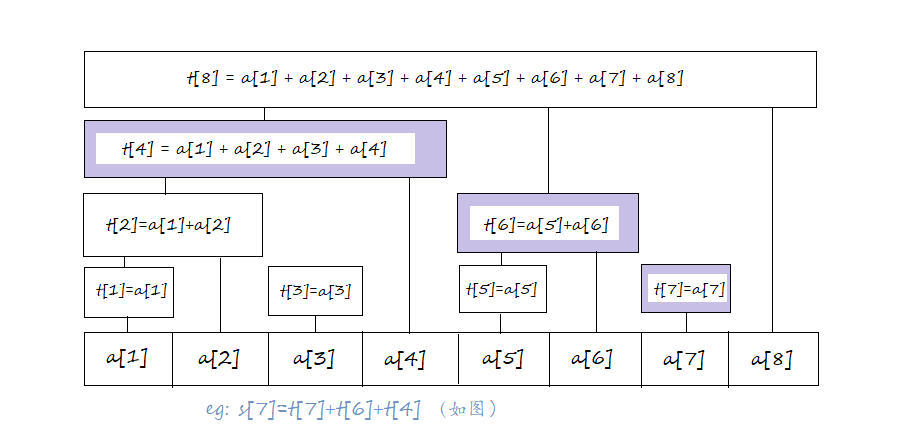
如图,对于查询 \(x\) 的前缀和:
从 \(t[x]\) 开始往前跳,有 \(c[x]\) 管辖 \(a[x-\operatorname{lowbit}(x)+1 \ldots x]\)
令 \(x \gets x - \operatorname{lowbit}(x)\),如果 \(x = 0\) 说明已经跳到尽头了,终止循环;否则回到第一步。
将跳到的 \(t\) 合并。
il int query(int x){
ri int s=0;
while(x) s+=tr[x],x=lowbit(x);
return x;
}
单点加&区间和
区间和用一下前缀和思想就好了
struct tree{
int tr[N],r;
il int lowbit(cs int x){return x&(-x);}
il void update(int x,cs int k){while(x<=r) tr[x]+=k,x+=lowbit(x);}
il int query(int x){ri int s=0;while(x) s+=tr[x],x-=lowbit(x);return s;}
il int ask(int l,int r){if(l>r) swap(l,r);return query(r)-query(l-1);}
}t;
signed main(){
ri int n=rd(),m=rd();t.r=n;
for(ri int i=1;i<=n;++i) t.update(i,rd());
for(ri int i=1,op,l,r;i<=m;++i){
op=rd(),l=rd(),r=rd();
op==1?t.update(l,r),0:(wt(t.ask(l,r)),putchar(10));
}
return 0;
}
区间加&单点查
考虑差分,对于差分数组 \(d\),\(a[x]\sum_{i=1}^x d[i]\)
区间 \([l,r]\) 加 \(k\) 相当于 \(d[l]+k\),\(d[r+1]-k\)
查询单点 \(x\) 相当于求 \(d[x]\) 的前缀和
struct tree{
int tr[N],r;
il int lowbit(cs int x){return x&(-x);}
il void update(int x,cs int k){while(x<=r) tr[x]+=k,x+=lowbit(x);}
il void operate(int l,int r,int k){update(l,k),update(r+1,-k);}
il int query(int x){ri int s=0;while(x) s+=tr[x],x-=lowbit(x);return s;}
}t;
signed main(){
ri int n=rd(),m=rd();t.r=n;
for(ri int i=1;i<=n;++i) a[i]=rd();
for(ri int i=1;i<=n;++i) t.update(i,a[i]-a[i-1]);
for(ri int i=1,op,l,r,k;i<=m;++i){
if((op=rd())==2) wt(t.query(rd())),putchar(10);
else l=rd(),r=rd(),k=rd(),t.operate(l,r,k);
}
return 0;
}
区间加&区间和
考虑差分&前缀和,对于差分数组 \(d\),\(a[x]\sum_{i=1}^x d[i]\)
于是,对于\(x\)的前缀和 \(s[x]\)
开两颗树状数组,分别维护 \(\sum_{i=1}^x (x+1) \cdot d[i]\) 和 \(\sum_{i=1}^x i \cdot d[i]\) 即可
struct tree{
int tr[N],r;
il int lowbit(cs int x){return x&(-x);}
il void update(int x,cs int k){while(x<=r) tr[x]+=k,x+=lowbit(x);}
il int query(int x){ri int s=0;while(x) s+=tr[x],x-=lowbit(x);return s;}
}t1,t2;
il void update(int l,int r,int k){
t1.update(l,k),t1.update(r+1,-k),t2.update(l,k*l),t2.update(r+1,-k*(r+1));
}
il int ask(int l,int r){
return (r+1)*t1.query(r)-l*t1.query(l-1)-t2.query(r)+t2.query(l-1);
}
矩形区域加&区域和(二维树状数组)
考虑二维差分&前缀和
对于差分数组 \(d[i][j]=a[i][j]+a[i-1][j-1]-a[i-1][j]-a[i][j-1]\)
对于其二维前缀和\(s[x][y]\)
开四颗树状数组
\(t1\) 维护 \(\sum_{i=1}^x \sum_{j=1}^y (x+1) \cdot (y+1) \cdot d[i][j]\)
\(t2\) 维护 \(\sum_{i=1}^x \sum_{j=1}^y i \cdot j \cdot d[i][j]\)
\(t3\) 维护 \(\sum_{i=1}^x \sum_{j=1}^y i \cdot d[i][j]\)
\(t4\) 维护 \(\sum_{i=1}^x \sum_{j=1}^y j \cdot d[i][j]\)
struct tree{
int tr[N][N];
il int lowbit(cs int x){return x&(-x);}
il void update(int x,int y,int k){
for(ri int i=x;i<=n;i+=lowbit(i)){
for(ri int j=y;j<=m;j+=lowbit(j)) tr[i][j]+=k;
} return;
}
il int query(int x,int y){
ri int as=0;
for(ri int i=x;i;i-=lowbit(i)){
for(ri int j=y;j;j-=lowbit(j)) as+=tr[i][j];
} return as;
}
}t1,t2,t3,t4;
il void update(int x,int y,int k){
t1.update(x,y,k),t2.update(x,y,k*x*y);
t3.update(x,y,k*x),t4.update(x,y,k*y);
}
il void Update(int x,int y,int xx,int yy,int k){
update(x,y,k),update(xx+1,yy+1,k);
update(x,yy+1,-k),update(xx+1,y,-k);
}
il int query(int x,int y){
return t1.query(x,y)*(x+1)*(y+1)+t2.query(x,y)
-t3.query(x,y)*(y+1)-t4.query(x,y)*(x+1);
}
il int Query(int x,int y,int xx,int yy){
return query(x-1,y-1)+query(xx,yy)-query(x-1,yy)-query(xx,y-1);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号