尝试matlab复现1990年论文STL: A Seasonal-Trend Decomposition Procedure Based on Loess中使用的LOESS算法
前言
最近在学习时间序列预测，需要使用STL算法对时间序列进行季节性趋势分离，而其中使用到一个称作LOESS的平滑算法。
本文是对1990年一篇有关时间序列分析论文中提及的LOESS算法的部分解读，并基于matlab实现
STL: A Seasonal-Trend Decomposition Procedure Based on Loess
数据来源
在google earth engine上获取2002年到2018年共17年的全球温度月(平均)数据，空间分辨率0.5°，时间分辨率1月
(获取数据需要特殊网络环境)
var d2 = ee.ImageCollection("ECMWF/ERA5/DAILY").filterDate("2002-01-01","2019-01-01");
var start_t = ee.Date("2002-01-01");
var sq = ee.List.sequence({
start: 1,
end: 12*17
});
var d2 = ee.ImageCollection(sq.map(function(m){
var start_d = start_t.advance(ee.Number(m).subtract(1),"month");
var end_d = start_d.advance(1,"month");
var new_d = d2.filterDate(start_d,end_d).mean()
.set("system:time_start",start_d.millis());
return new_d;
}));
var TMP = d2.select("mean_2m_air_temperature");
Export.image.toDrive({
image: TMP.toBands(),
crs: "EPSG:4326",
dimensions: "720x360",
region: ee.Geometry.Rectangle([[-180,-90],[180,90]],null,false),
fileNamePrefix: dataname[4]
});
文件大小186MB，文件格式tif，可以在matlab中使用imread(filename)直接读取
算法解读
LOESS基于局部加权回归(Local Weighted Regression)原理，对散点图的某个x坐标进行局部的而非全局的加权回归，而后估计在给定x坐标上的值。
LOESS包含两个关键参数，q表示在给定x坐标周围参与局部多项式回归的近邻点个数，d表示进行局部多项式回归的多项式次数。
这里的x做可以取连续值，因为它只需计算与最近的采样点的距离即可得到回归权重，通过近邻点来估计当前位置点(类似KNN的思想)。
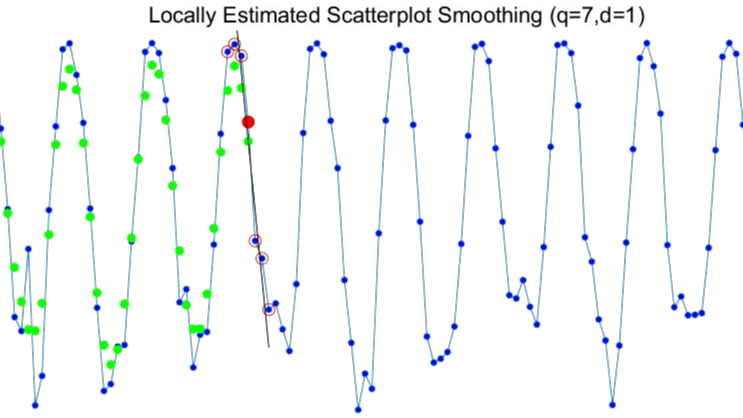
下图演示了参数为q=7,d=1的LOESS平滑过程
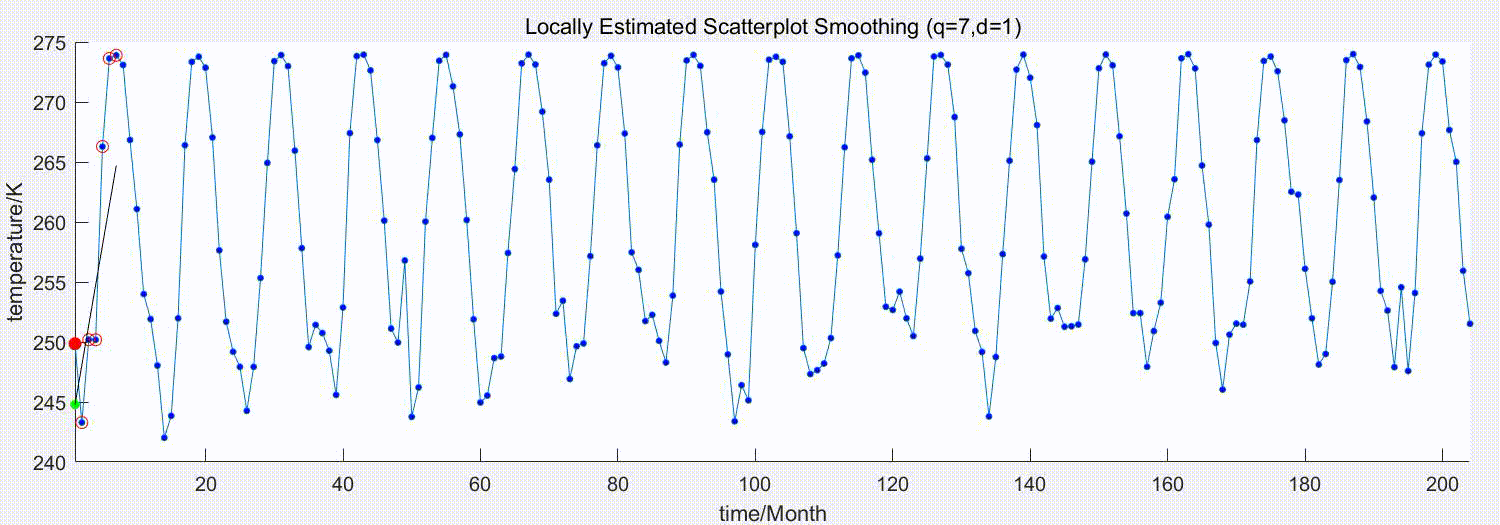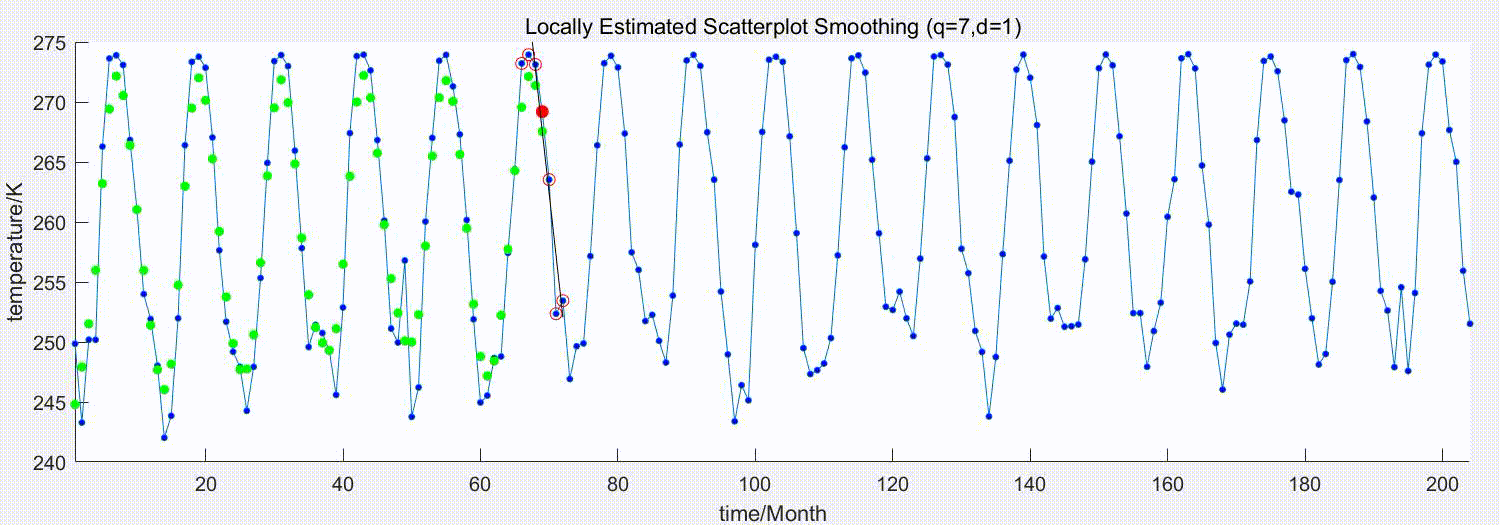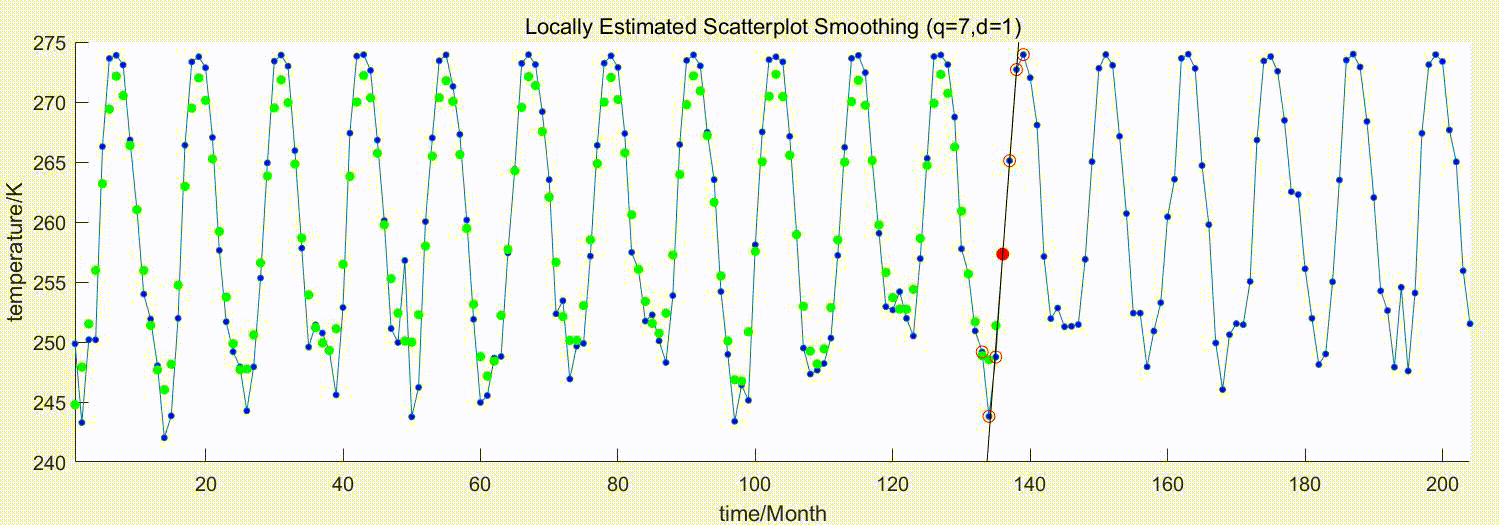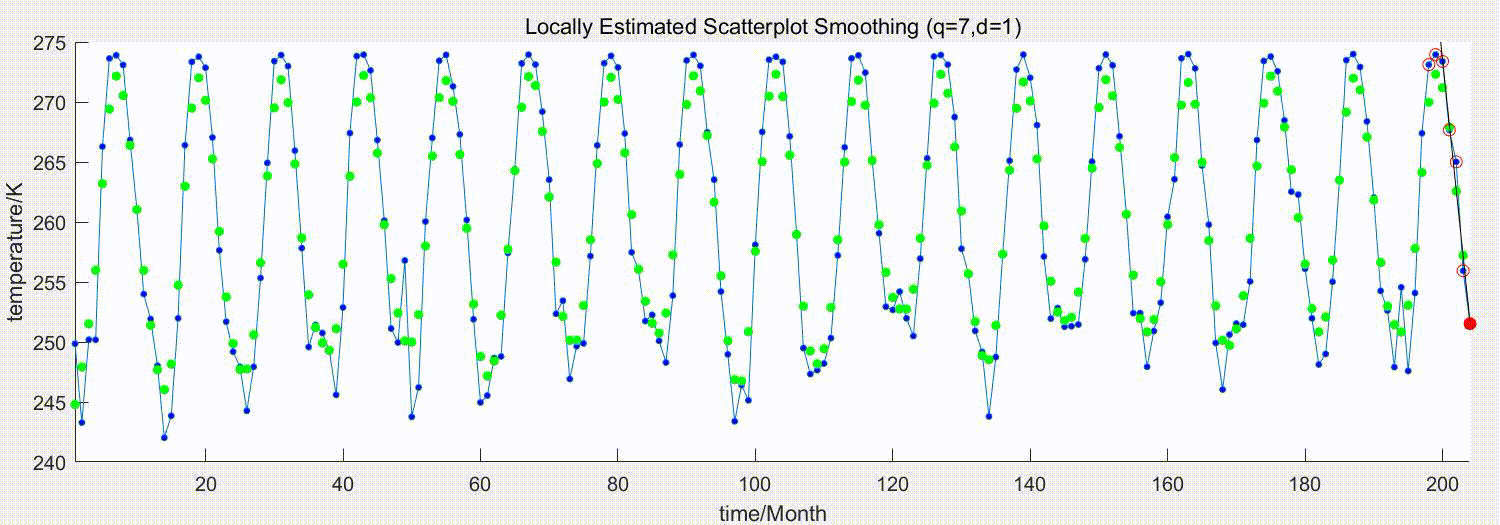
蓝点为原始序列，红点为待估计的原始序列点，红圈为选中参与局部回归的近邻点，绿点为平滑后的估计值
算法实现
读取tif文件并取其中一个像素点的时间序列，该序列长度为\(12\times 17=204\)，为17年的月采样序列
data = imread("TMP_monthly.tif");
y = reshape(data(1,1,:),1,[]);
x = 1:numel(y);
% 这里约定x和y为行向量
定义q和d，这里选择以7个近邻点做1次多项式(线性)回归
q = 7;
d = 1;
首先对x和y进行一个缩放和中心化(Z-Score标准化)，目的是为了在计算最小二乘解时避免数据溢出
实测如果不进行缩放，在x值超过120时会导致最小二乘解结果产生偏差，即便数据以64位浮点的double类型存储也无法解决，而预先进行缩放是个人实测有效的方法，不过要注意在最后进行反变换恢复成原始序列。
y_mean = mean(y);
y_std = std(y);
x_mean = mean(x);
x_std = std(x);
ys = (y-y_mean)/y_std;
xs = (x-x_mean)/x_std;
在遍历序列中每个采样点之前声明一个数组用于存储平滑后的序列
yhat = nan * ones(size(ys));
循环体中的内容如下
for i = 1:numel(xs)
xi = xs(i);
% 1. 选择与xi近邻的q个y值不为nan的点
% 2. 计算近邻元素权值
% 3. 计算加权回归系数
% 4. 计算估计值
end
第一步的操作是为了保证时间序列存在空缺值的情况下仍能进行，LOESS的基本逻辑就是采用最近邻点进行回归估计，因此能有效填补空缺值。
实现思路：使用mink()函数来取得q个x上距离abs(xs-xi)最小值点，循环判断这些点的y值是否存在nan，如果存在，则每次多取一个点(stq加1)，直到取到q个符合要求的近邻点。其中I为近邻点的索引数组，B为近邻点x值与\(x_i\)的距离数组.
stq = q;
[B,I] = mink(abs(xs - xi),stq);
idxs = ~isnan(ys(I));
I = I(idxs);
while numel(I)~=q
stq = stq + 1;
[B,I] = mink(abs(xs - xi),stq);
idxs = ~isnan(ys(I));
I = I(idxs);
end
B = B(idxs);
上述得到的B中的元素，为从小到大排列的距离值，与索引序列I中的元素一一对应，B(1)是与\(x_i\)最近元素的x轴距离，相反B(end)是与\(x_i\)最远距离。通过B可以计算近邻点的权值，但首先要将B整体除以最远距离B(end)进行[0,1]范围归一化
weight = W(B/B(end));
function res = W(u)
idx1 = u>=1;
idx2 = u<1 & u>=0;
idx3 = u<0;
res = zeros(size(u),"like",u);
res(idx1) = 0;
res(idx2) = (1-u(idx2).^3).^3;
res(idx3) = 0;
end
这里的W函数是文献中采用的三次权函数，有的文献中采用指数
计算得到的weight一般是像如下所示的以1开头逐步递减至0的序列
weight =
1.0000, 0.8930, 0.8930, 0.3485, 0.3485, 0.0000, 0.0000
它们就是对数组I对应索引元素的权重，比如当前循环处理第9个元素，那么其近邻的7个点从距离由近到远的元素索引和距离分别是
I =
9, 8, 10, 7, 11, 6, 12
B =
0, 0.0169, 0.0169, 0.0339, 0.0339, 0.0508, 0.0508
即最近的点赋予最高的权值，而在q之外的点赋予\(0\)的权值
然后是计算加权回归系数，先根据多项式阶数d构造线性方程组\(Ax=b\)中的A矩阵xmat，它是由近邻点x值序列构造的矩阵，其第\(1\)列为常数列，第\(2\)列为\(1\)次项，……，第\(k+1\)列为\(k\)次项
\(Ax=b\)中的b向量ymat为近邻点的y值序列
调用matlab的lsqminnorm(A,b)函数计算最小范数最小二乘解，相比A\b具有更高的数值稳定性，同时相比pinv(A)*b也有更高的计算效率
xmat = ones(q,d+1);
for k = 1:d
xmat(:,k+1) = xs(I).^k;
end
ymat = ys(I)';
tp = xmat' * diag(weight);
what = lsqminnorm(tp * xmat, tp * ymat);
最后使用回归系数估计\(x_i\)点的\(\hat y\)值
xpre = ones(1,d+1);
for k=1:d
xpre(k+1) = xi^k;
end
yhat(i) = xpre * what;
完整代码(包含可视化)
clear;
clf;
data = imread("TMP_monthly.tif");
y = reshape(data(1,1,:),1,[]);
x = 1:numel(y);
q = 7;
d = 1;
%% LOESS(x,y,q,d)
y_mean = mean(y);
y_std = std(y);
x_mean = mean(x);
x_std = std(x);
ys = (y-y_mean)/y_std;
xs = (x-x_mean)/x_std;
set(gca,"position",[0.05,0.12,0.93,0.8])
set(gcf,"position",1000*[2.6903 -0.2103 1.000 0.3500]);
set(gcf,"name","Temperature");
xlabel("time/Month");
ylabel("temperature/K");
hold on;
plot(xs*x_std+x_mean,ys*y_std+y_mean,'-o','markersize',3,'MarkerFaceColor','b');
xlim([xs(1)*x_std+x_mean,xs(end)*x_std+x_mean]);
title(sprintf("Locally Estimated Scatterplot Smoothing (q=%d,d=%d)",q,d));
xlabel("time/Month");
ylabel("temperature/K");
axlim = axis;
yhat = nan * ones(size(ys));
for i = 1:numel(xs)
xi = xs(i);
% 选择q个y上不为nan的值
stq = q;
[B,I] = mink(abs(xs - xi),stq);
idxs = ~isnan(ys(I));
I = I(idxs);
while numel(I)~=q
stq = stq + 1;
[B,I] = mink(abs(xs - xi),stq);
idxs = ~isnan(ys(I));
I = I(idxs);
end
B = B(idxs);
% 近邻元素权重
weight = W(B/B(end));
% 最小二乘回归
xmat = ones(q,d+1);
for k = 1:d
xmat(:,k+1) = xs(I).^k;
end
ymat = ys(I)';
tp = xmat' * diag(weight);
what = lsqminnorm(tp * xmat, tp * ymat);
xpre = ones(1,d+1);
for k=1:d
xpre(k+1) = xi^k;
end
yhat(i) = xpre * what;
% 绘图部分
if exist("selp","var")
delete(selp);
delete(selp1);
delete(regc);
end
selp = plot(xs(I)*x_std+x_mean,ys(I)*y_std+y_mean,'ro');
plot(xi*x_std+x_mean,yhat(i)*y_std+y_mean,'g.',"markersize",16);
selp1 = plot(xi*x_std+x_mean,ys(i)*y_std+y_mean,'r.',"markersize",22);
% 绘制回归曲线
xpre = ones(numel(I),d+1);
for k=1:d
xpre(:,k+1) = xs(I).^k;
end
pdy = xpre * what;
regc = plot(xs(I)*x_std+x_mean,pdy*y_std+y_mean,'k');
axis(axlim);
drawnow;
% pause(0.2);
end
function res = W(u)
idx1 = u>=1;
idx2 = u<1 & u>=0;
idx3 = u<0;
res = zeros(size(u),"like",u);
res(idx1) = 0;
res(idx2) = (1-u(idx2).^3).^3;
res(idx3) = 0;
end
