等距螺旋森林的迷路指南
t
通过阿基米德螺旋和渐开线的铺垫，相信您已经对等距螺旋有了一个大致的了解。
再来回顾一下：直线运动与圆周运动的叠加，可以形成螺旋曲线，传统意义上的螺旋线只是螺旋曲线的一部分。
直线与圆周的位置关系从高到低的可分为相切、相交、穿过圆心，如图1中的五种情况。
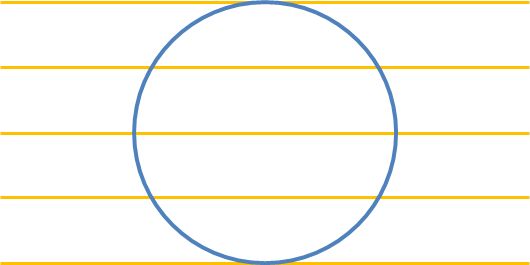
图1 直线与圆周的位置关系
圆周可以顺时针或逆时针旋转，直线运动分为从左到右，或从右到左。对所有情况进行排列组合，可以得到20种方案。通过对比可以发现顺时针旋转搭配从左到右直线运动的轨迹，等同于逆时针旋转搭配从右向左直线运动的轨迹，因此，单纯考虑从左向右的直线运动，图形的组合可以缩减一半，一共有10种组合。
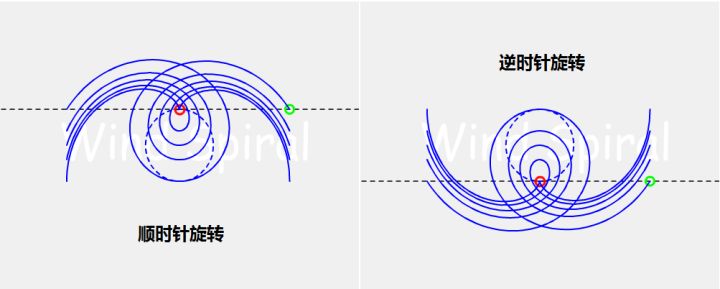
图2 等距螺旋的十种组合
若将图2中两部分的图形看作是旋转180°的结果，则图形的组合还可以缩减为5种。但不建议这样缩减，因为同一位置的直线运动顺时针旋转与逆时针旋转二者的曲线是有相关性的，如图3所示。
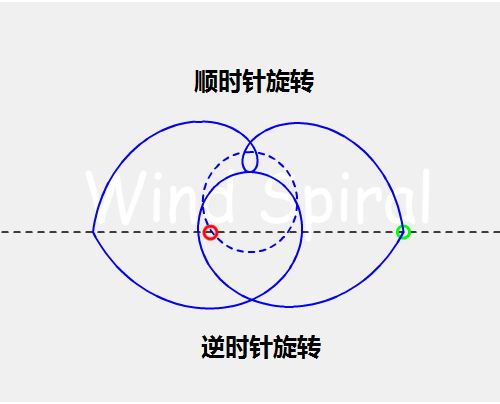
图3 顺/逆时针旋转的位置关系
对于同样的水平方向从左向右运动，图3中的上半部分为顺时针旋转产生的轨迹，下半部分为逆时针旋转所产生的轨迹，两条轨迹在近地点位置精确相切。
等距螺旋关注的是直线运动与圆周运动的关系，而传统的螺旋线仅是对射线运动的轨迹进行的分析。通过改变直线与圆周的位置关系，我们可以很容易发现传统的螺旋线在认识上存在的较多缺失。
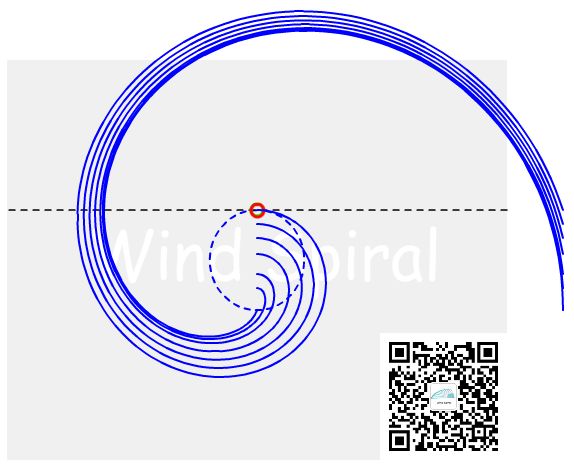
图4 等距螺旋模拟传统螺旋
图4中从近地点位置（直线距圆心的最近点）绘制的多条等距螺旋。圆周最下部引出的螺旋为渐开线螺旋，从圆心引出的螺旋为阿基米德螺旋。图4中的直线运动速度等于圆周的旋转速度，图中所有的螺旋从同一个竖直位置旋转一个周期到达同样的竖直位置。即同一旋转周期内直线运动相同的距离，增加旋转周期后的效果同样符合这一条件，所以，它们都属于等距（离外扩）螺旋。
从等距螺旋的公式分析（目前还未涉及到）可以知道，等距螺旋又可以称为等速度比螺旋。直线速度与圆周的旋转速度之间的比值，决定了螺旋外扩的快慢。以阿基米德螺旋为例，若直线速度与圆周速度比从0.2开始增加至1.4，每0.2为间隔，绘制的一系列阿基米德螺旋如图5所示的样子。
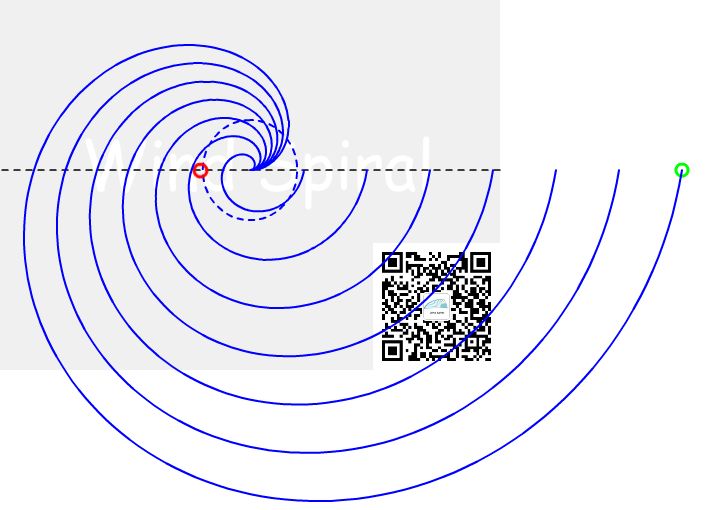
图5 不同速度比的阿基米德螺旋
提高直线与圆周的相交高度，螺旋按比例外扩的特性是相同的。
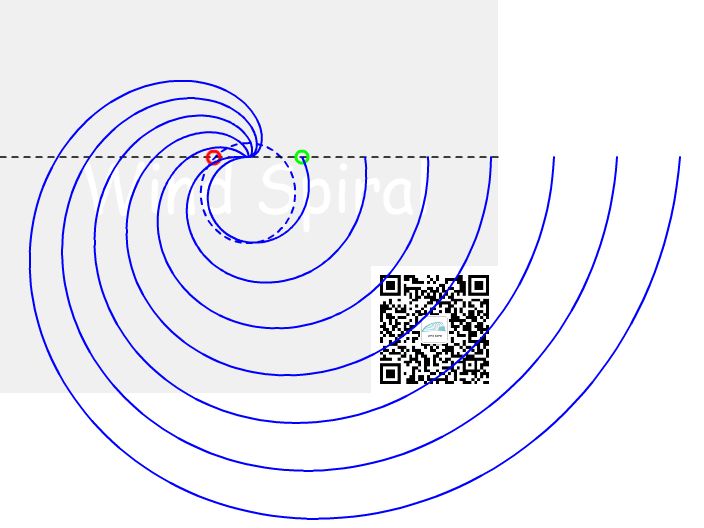
图6 不同速度比的等距螺旋
真正比较迷惑人的情况是多种运动方向、多种相交高度的螺旋堆叠在一起的情况，如图7所示。
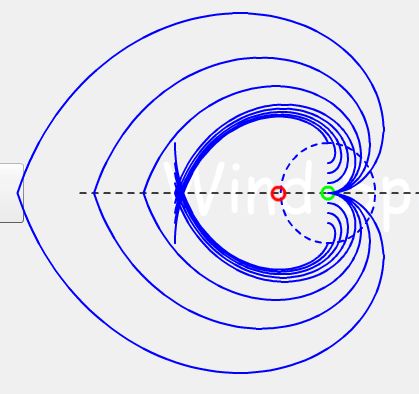
图7 多种等距螺旋的重叠效果。
图7中，上半部分的螺旋与下半部分的螺旋主要的区别是旋转的方向不同。由于螺旋线可以通过不同运动方向的搭配来实现，因此，它是一种运动的轨迹，并不直接代表某一种单一的运动方式。
通过对等距螺旋的基本位置关系与运动关系的分析，可以相对容易的对螺旋的成因进行理解，从而为进一步的公式推导铺平道路。
从等距螺旋的位置关系来看，阿基米德螺旋是从圆心引出的螺旋，渐开线螺旋是从圆周上引出的螺旋，并且对速度有特定的要求，因此，它们二者均是等距螺旋的特例。在其它直线与圆周相交所产生的螺旋中，还有一种非常特殊的对速度有要求的螺旋——风螺旋，将出现在我们的视野，等距螺旋的公式就是由风螺旋的公式演化而来，敬请期待！
更多内容请关注微信公众号“风螺旋线”及知乎“等距螺旋的算法之路”专栏，欢迎互动交流！
以上所用图形的动画演示文件下载地址：
