论渐开线的“正确”打开方式

 

关于渐开线，最易于理解的解释是：将绕在圆柱上的细线拉直打开，线头所形成的轨迹即是渐开线。

更专业的解释是：在平面上，一条动直线（发生线）沿着一个固定的圆（基圆）作滚动的过程中，此直线上任意一点的轨迹，称为此基圆的一条渐开线。

 

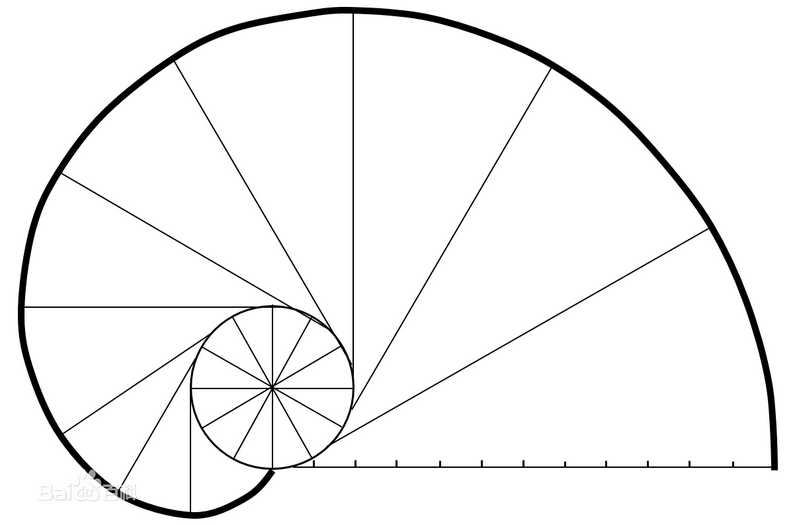
图1 渐开线螺旋

渐开线与阿基米德螺旋在现有公式上是不相融合的，主要原因是二者的描述方式有着较大的差别，因此，在公式建立时采用了不同的分析思路。

按照直线运动与圆周运动相叠加的思路来分析：直线与圆周相切（或者是相束缚）于一点，并随着圆周进行旋转，直线上有一动点，沿着与旋转相反的方向进行运动，每旋转一周，直线上移动的距离恰好等于一个周长时，动点所形成的轨迹就是渐开线。

 

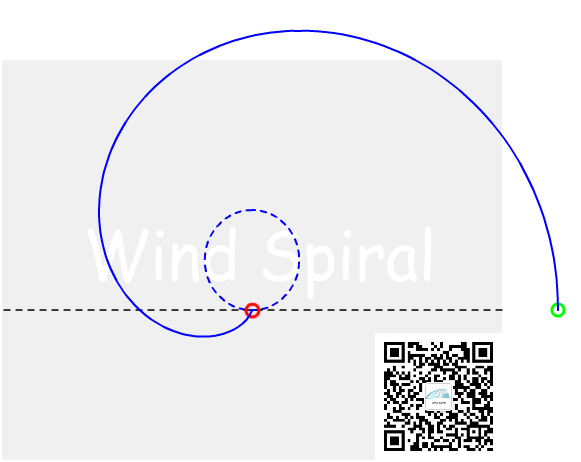
图2 运动轨迹所形成的渐开线

如图2所示，有一水平直线相切于圆周的底部（红色点位置），圆周顺时针旋转。有一绿色小球从切点开始自左向右沿直线运动，圆周旋转一周，绿色小球移动一个周长的距离。对绿色小球的运动轨迹进行记录，可以得到图2中蓝色的渐开线。

 

图2中实质上使用的是射线运动与圆周运动相叠加来产生的渐开线，若以完整的直线运动来表示渐开线曲线，可以看到如图3中的情况。

 

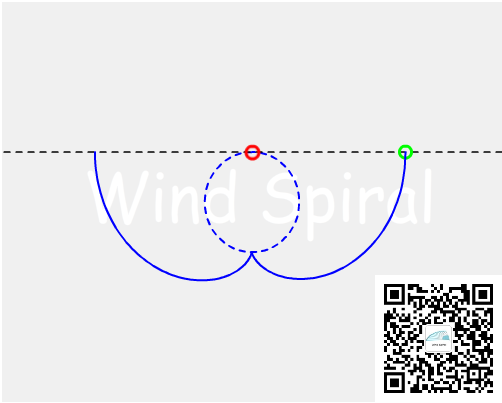
图3 直线运动产生的“两段”渐开线

绿色小球从屏幕左侧向右侧移动，初始位置距离红色小球半个圆周的长度，圆周逆时针旋转，绿色小球的轨迹为两条渐开线，这两条渐开线在圆周位置处相连接在一起，并且是相切关系。若将绿色小球的位置放的更远一些，可以形成较为完整的渐开线，并且可知，顺时针外扩的渐线与逆时针外扩的渐开线实际上是同一个运动轨迹所产生。

通过以上分析可以知道渐开线是直线运动与圆周运动相切时所产生的轨迹，直线运动的速度与圆周运动的速度必须相同，旋转方向相反。在上面的例子中，若直线运动的方向不变，只是改变圆周的旋转方向，则曲线的形态会完全不同，如图4所示。

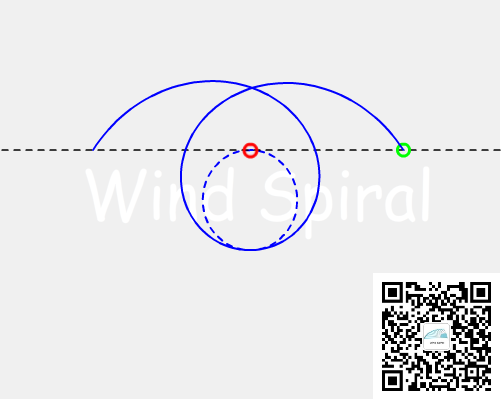
图4 从左向右移动与顺时针旋转的轨迹

通过图3与图4的对照可以看到，即使直线与圆周处于同一个相切位置，若旋转的方向不同，得到的轨迹将大不相同。以往的分析中，缺少对圆周与直线的位置关系、运动方向的分析，因而，得出的结论并不能够准确体现出螺旋的本质特征。

从直线与圆周的位置关系来分析，阿基米德螺旋是直线穿过圆心的产物。

直线与圆周相交，还会产生更多样的螺旋曲线，这些曲线均体现为同一个旋转周期内直线移动相同的距离，可以用共同的名称“等距螺旋”来命名，根据等距螺旋的参数来分析，匀速直线运动并不是必需的，直线运动的速度与圆周运动的速度比为固定值，才是它们的本质特征，因此，等距螺旋又可以称为等速度比螺旋。

在等距螺旋的框架下，阿基米德螺旋、渐开线螺旋、风螺旋 三者是等距螺旋的典型特例，可以用相同的公式来进行描述，且具有相似的特性。未来我们将对此话题进行深入的讨论，敬请关注。

如果您觉得本篇文章对您有所启发，请积极转发，未来我们将对此话题进行深入讨论，欢迎持续关注风螺旋线公众号，寻找更多答案。

本文相关螺旋的 flash版动画演示下载地址：

https://pan.baidu.com/s/1jY82o8C4KTN5As9hp621Dw

我为等距螺旋代言！