风螺旋线的外扩算法
风螺旋线的外扩算法
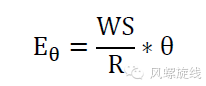
WS代表风速，R（大R）表示转弯率，Eθ表示转过某角度（θ）后得到的偏移量。
这个公式反过来看，会是这样的：
这样的式子，它的含意是什么呢？要得到一个指定的外扩距离Eθ，只需要将整个风螺旋线旋转θ角即可。
真得是这样么？为什么从来没有人告诉过我们呢？
我想说：真的是这样的，真的是这样的，真的是这样的。
（重要的事情说三遍，好了，证明给你看）
之所以没有人把这个公式反过来看，基于三点原因：
-
不知道外扩的方向是朝哪个方向。
-
不知道旋转的中心是指的哪一个。
-
没有意识到，反过来看时同样具有现实意义。
先来回答第一个问题。风螺旋线切线必然与某个Eθ向量相垂直，因为从最初的画法来看，我们是以不同的Eθ做半径，画出的圆弧相衔接得到风螺旋线，因此，每一个风螺旋线上的点都与一个特定的Eθ有关。
通过风速三角形在转弯过程中的分析，我们知道，能够到达最外侧边界的（换句话说是能伸得最远的那个）Eθ，必然与风速向量方向一致，与地速向量相垂直，此时地速向量与空速向量的夹角为最大偏流角DA，地速向量就是风螺旋线的切线方向。如下图所示：
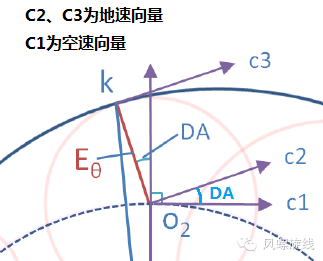
Eθ的外扩方向找到了，接下来旋转的中心点其实就是标称圆的圆心点，因为我们计算θ角时，一直都是基于标称圆的圆心来考虑的。
于是可以用一个例子来看这个问题：
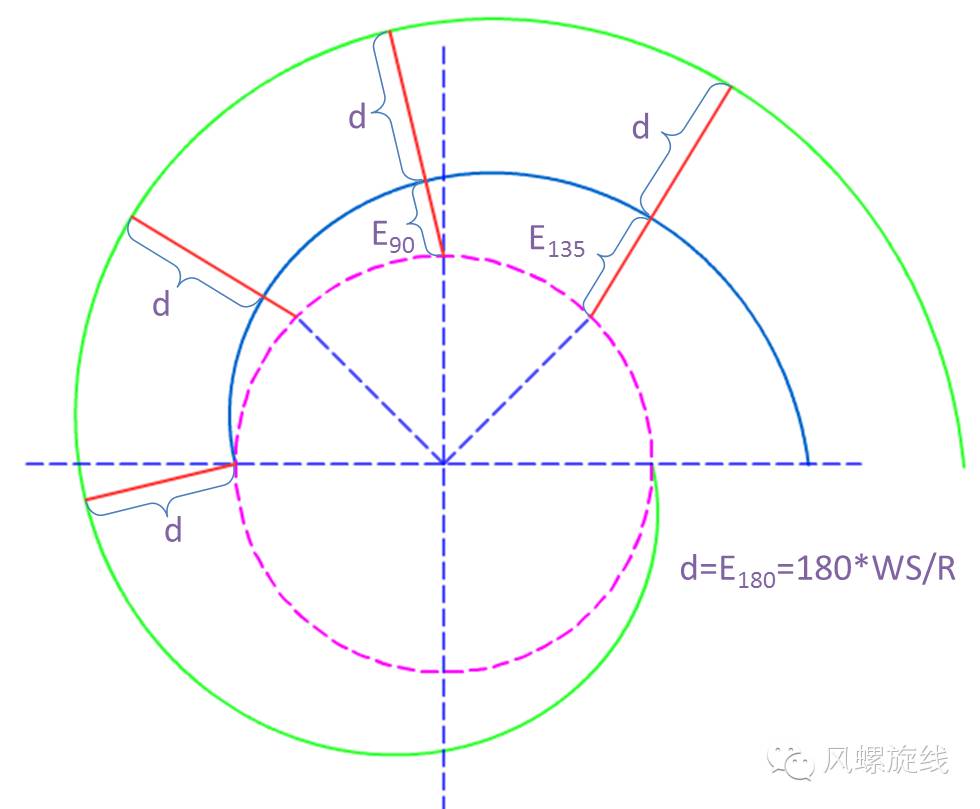
上图中绘制了两条初始角度相差180°的风螺旋线，按照之前的分析，可以看到，两条风螺旋之间的距离是沿着Eθ方向来进行外扩的。
如果需要外扩指定的距离，在手工绘图的情况下，可以采用旋转风螺旋模板的办法来实现，在计算机绘图的情况下，直接按照Eθ方向外扩即可。
上图中内侧风螺旋线的起点处，需要外扩时，仍必须沿Eθ方向进行量取。此时内侧风螺旋的Eθ值为零，但与之相关的风速向量却是存在的。在绘制保护区副区起点时，经常会感觉它比主区的风螺旋线“早”那么一点点，其实就是这个原因，早的那一点点实际上就是一个偏流角的距离。
回想最初设计出风螺旋线的那些老专家们，那时候的计算机应用肯定没有现在这么便捷，从分段圆弧模拟的作图方式就能印证这一点。但是在那样的困难环境下，他们却想出了风螺旋线这样最为“保守”的人造曲线，并且在保护区的绘制中用模拟画法实现了绝大部分的内容。
今天我们通过计算机技术，用“算法”概念来实现过去的设计理念，其中频繁出现的“巧合”，不禁让人感叹过去设计的巧妙。曾经很长时间里，我们被切线、外扩的算法困扰良久，各种复杂的计算方法更是将深入的讨论挡在了门外。我想这绝不是老一辈专家们的本意，技术手段的局限使然。
回到最初的风速三角形，重走一遍公式推演的道路，才发现，原来最大的秘密就藏在最初的那个地方。
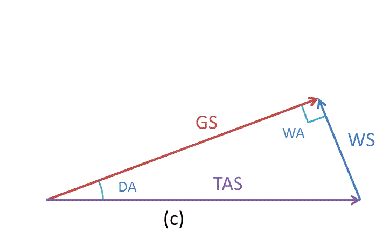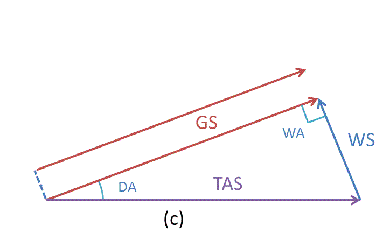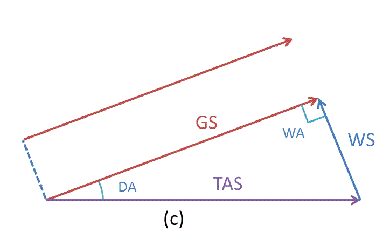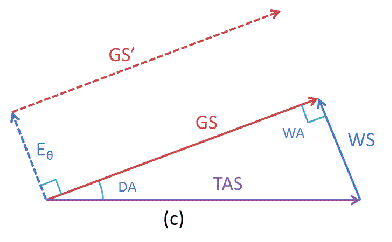
向老专家们致敬！
（to be continue 话题未完，敬请期待~~）
感谢大家关注《风螺旋线》微信公众号，历史信息中介绍了两种风螺旋线切线的计算方法，加上本篇风螺旋线的外扩方法，相信您已经具备了实现离场转弯保护区、PBN flyby、flyover转弯保护区、复飞转弯保护区自动化绘制所需的基础理论，相关论文目前尚属空白，期待大家发挥聪明才智，多多讨论相关的算法问题。
风螺旋线函数目前已在Flash系统中实现，尚缺乏在其它系统如CAD中实现的过程，建议有实力的读者将风螺旋线做成CAD插件，共享出来方便大家使用，相关话题也是一个很好的论文研究方向，期待大家深入讨论。
风螺旋线外扩算法的论文已于2017年元月发表于《飞行学院学报》，引文格式：
微信扫一扫
关注该公众号
