风螺旋线的切线（二）
风螺旋线的切线（二）
数学中的难题用计算机来解决时，可以采用一种简单粗暴的运算方法来计算结果，这种方法就是——迭代运算。
迭代运算的原理就是先粗略的计算出一个结果，然后和目标要求相比较，找出差距，调整后，重新计算，重复这个过程直到运算精度满足要求为止。
在PBN保护区绘制时，常见的一种情况就是从下一航路点绘制风螺旋线的切线做为最晚标称航迹，在此基础上外扩15°做主区外边界。（下图中的红线）
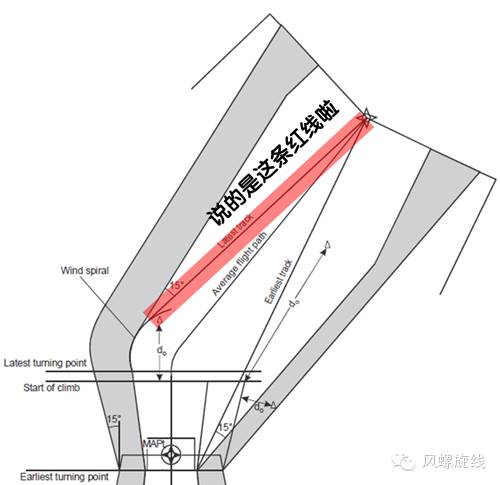
此种情况与之前提到的绘制平行标称航迹的算法的区别在于，这里需要让切线通过指定的点，之前的讨论中切线与转弯后的标称航迹相平行。
计算的过程简单来说是这样滴：
-
先从指定的点，向标称转弯圆弧绘制切线。在这里，转弯半径、指定点到标称圆圆心的距离 是已知条件。根据反余弦函数，可以得到与风螺旋切线有关的θ角。
-
从θ角对应的风螺旋线上点画切线，切线的角度是θ-DA+90（上次讨论的内容）。将首次得到的切点与曲线外的指定点进行连线，找出切线与连线之间的夹角（假设是Ω）。
-
将Ω角的值累加到θ角中，再次计算出风螺旋线上的点，计算切线角度、计算指定点连线的角度，算出差值。
-
重复上面的过程，直到切点与指定点之间的连线与切点处真实的切线近似重合为止。
迭代计算的路径如下图中所示：
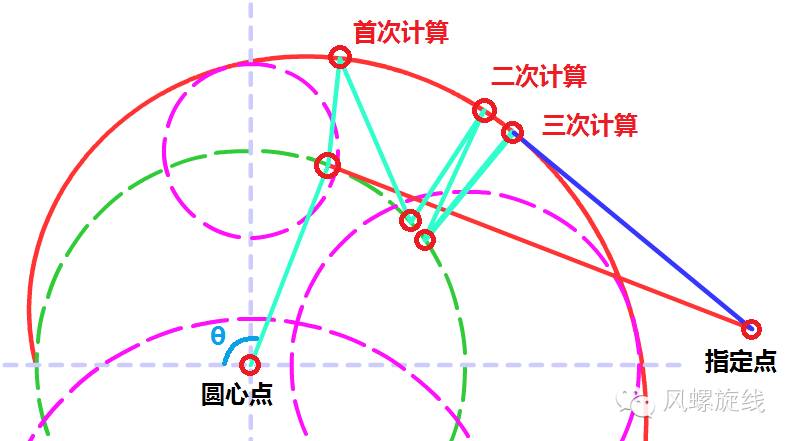
图中圆心点出发的浅蓝色（浅绿色？）线条是迭代计算的路径，标称圆弧上的点与风螺旋线上的点是1-1对应关系，因此可以在每次找出切线与连线的夹角后，直接累加到θ角中，实现的是精确逼近算法。这样的过程在计算机中大约需要多少次呢？
从实际测试的结果来看，距风螺旋线稍远的位置上，通过三次计算即可达到0.0000001以内的精度，小数点后有６个０。精度级别的提升主要与位置有关，比如下图中四次迭代计算，精度到了小数点后13位。
千万分之一的精度换算成角度数大约是0.000006度，如果转弯半径为50公里，这个精度级别大约在0.005米，也就是半厘米以内。
风螺旋线切线计算的两种方法就是这样，第一种切线与标称航迹平行，直接用加减法即可得出θ角。第二种切线过指定点，用迭代算法进行解决，迭代计算四次左右即可达到千万分之一级的精度。
有了这两种方法，已经可以解决大多数只有一侧风螺旋线的计算问题。如果存在多条风螺旋线，则需要讨论公切线的算法，留到下次再来讨论。
风螺旋切线的“世界性”难题就这样解决了？难以至信，我自己也是这样的感觉。
与此话题相关的论文已发表于2014年第8期的《空中交通》杂志，该论文的引用格式如下：
刘崇军.风螺旋线的深度分析[J].空中交通,2014(8):80-84.
往期话题请在关注微信公众号“风螺旋线”后，通过历史消息查看。
微信扫一扫
关注该公众号
