风螺旋的核心是旋转
风螺旋的核心是旋转
还记得上次说到的传统风速三角形吗？（其实是前天说的）动态的看会是下面的情形：
受侧风的影响，随着时间的推移，实际的轨迹线与标称的轨迹线会越来越远。
如果把这个三角形绑到一根绳上，抡起来看，会是什么样呢？
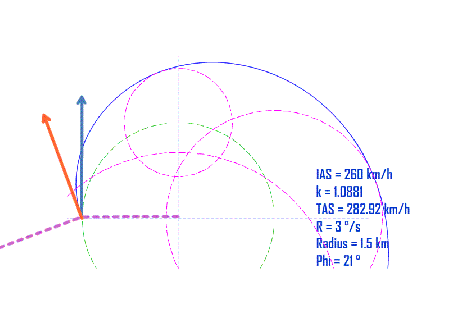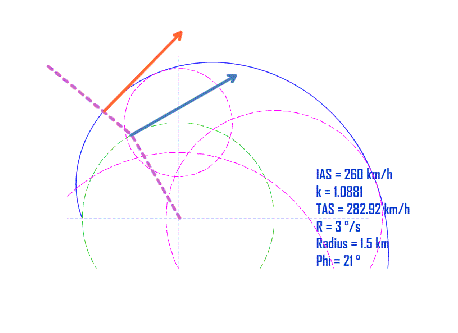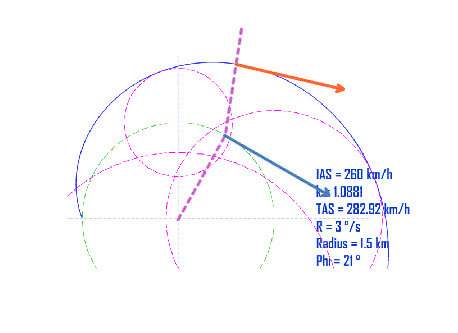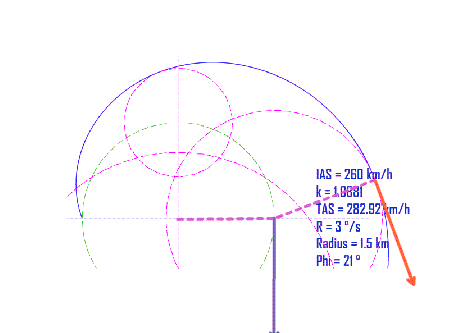
首先三角形肯定会散架，红色GS箭头被风吹的向外飘移，距离蓝色TAS箭头会越来越远。因为外飘的速率与转弯率相对应，所以看像起来是均速的外移。
GS箭头是按照最大的偏流角移动，所以始终与假想的TAS箭头夹角为最大偏流角DA。
为什么说是假想呢？
首先，现实世界找不到随时与地速相垂直的全向风，即始是存在这样全向变化的风，GS箭头也会因为要跑更多的路，因此，会滞后于在标称圆上移动的TAS箭头（风速在里既不增加地速也不减少地速，只是改变地速的方向）。所以这种固定角度的运动效果只是假想。
GS箭头的轨迹是不是看起来很眼熟？
没错，外侧的轨迹就是风螺旋线。
这和传统的的方法似乎不一样啊？传统的方法是分段圆弧然后画包络线，就像下面看到的那样。
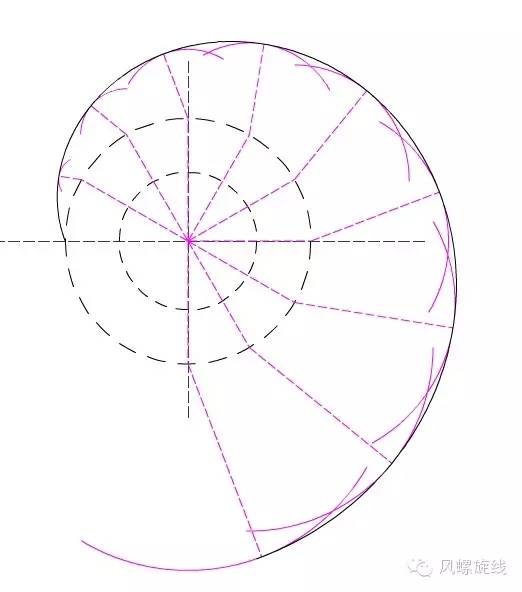
应该说只是思路不同，本质上却是一样的。
比较一下：
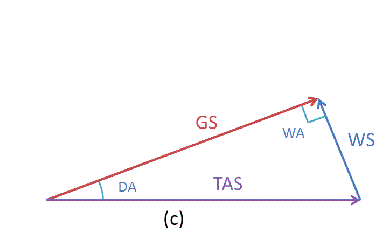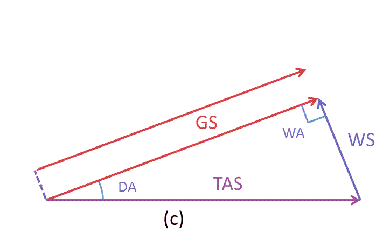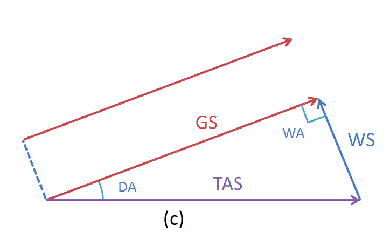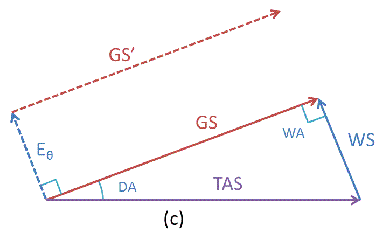
TAS与转弯半径垂直，GS外扩速度与转弯率相对应（Eθ=θ*w/R），每一个外侧边界点都是按最大偏流角计算得到。
为什么非得和速度三角形扯上关系呢？
这和后面的关键公式的推导有很密切的关系，这里只要记住一点，速度三角关系放在旋转的空间里，就会得到风螺旋线，它们实际上是统一的。
再往后聊的时候，你就会发现，与风螺旋有关的很多内容都是和旋转有关。
今天就到这里，下次再聊。
微信扫一扫
关注该公众号
