世界是几维的？
如果弯曲（旋转）是一种维度，世界大不相同
世界是几维的？三维的？四维的？11维的？
开始讨论之前先来想一下，维度的定义是什么？它有什么特点？
通常我们所说的维度指的是用来描述空间的尺度，如果把时间也作为了一个维度，我们能够直接感知到的就是四维空间（上下、左右、前后、早晚）。
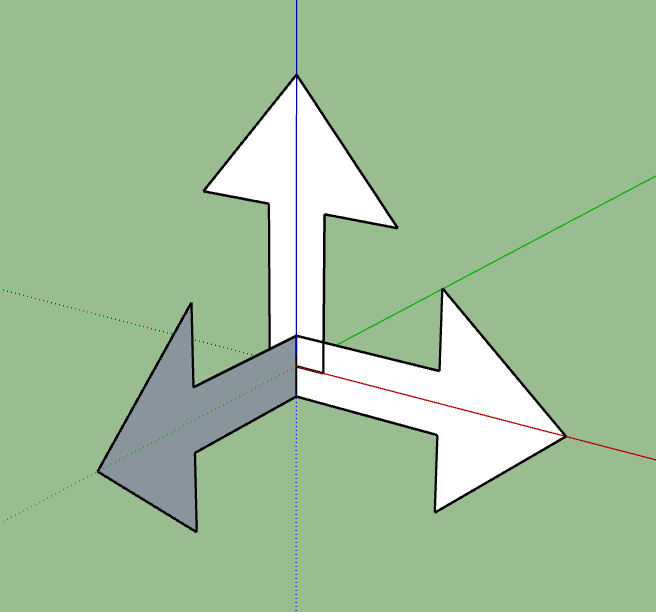
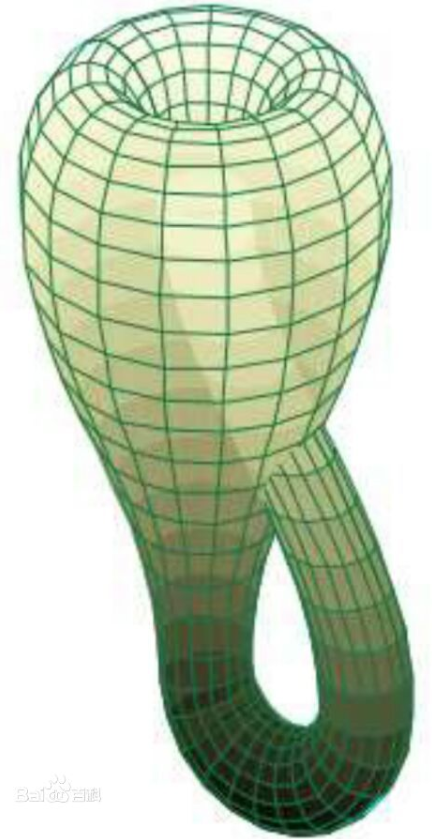
如果直接用三维空间来定义我们的世界，显然很多几何形状是无法解释的通的，比如“莫比乌斯带”和“克莱茵瓶”。
从0维的点到三维空间，可以发现，维度升高时，会经历从点到线、再到面再到“体”的变化。从高维度降低时，高维度的空间投影到低维度上会缩减成线或是点。时间在三维空间上的投影无法观察（物质的衰败算是可以看到的），因此，时间作为一个维度来理解并不合适。
传统中对于维度的定义都是直线式的，这导致我们对于复杂结构的描述缺少必要的参数，同时在数学的表达上陷入了复杂公式的泥沼中。
当世界以旋转（弯曲）的方式出现的时候，我们也应该以旋转的思维来理解它。正如我们在等距螺旋中所看到的一样，原以为的均速运动形成的螺旋，实际上是速度比保持不变所形成。
以旋转（弯曲）为维度，重新来看一下，我们的世界，将是下面的样子：
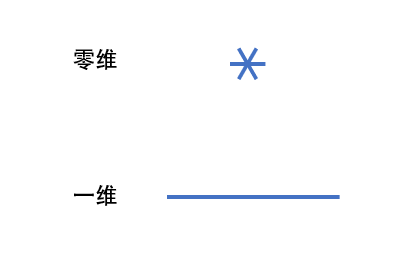
零维——是一个点。通常意义上，它本身并无大小，无论放大还是缩小，对它来说没有意义。
一维——点在单一方向上发生移动，移动的轨迹就一条直线。对于一维的物体，可以用长度来进行描述。
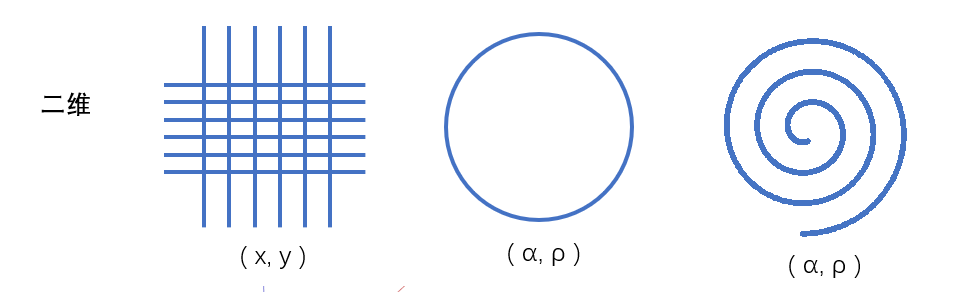
二维——除了前后移动，还可以左右移动时，就像是横竖交织的线条，最终可以形成一个平面。这就是二维的空间，从测量的角度来说，除了长度以外开始有了宽度。
如果没有外力做用，物体会保持静止或均速直线运动（一维空间）。只有当受到侧向力量的影响，运动方向才会发生改变，比如受引力的影响，直线轨迹会变成圆或者螺旋。所以弯曲的曲线是受外力作用而形成，这个外力可以用一个维度来表示，就是旋转的维度。
从这里开始，我们对于维度的认识开始分化。
圆周运动需要有引力来支持才能保持，从这一点上看，它与直线相比是增加了一个维度。螺旋与圆的关系，就是螺旋中存在外扩的直线速度。直线运动不需要有外力来维持，所以螺旋与圆相比，是同一个维度。
三维空间
二维世界向三维世界扩展时，有两种选择，第一种是增加一个直线维度，第二种是增加一个旋转的维度。
1、增加直线维度
增加一个直线维度后，前面提到的二维形状是什么样子。
平面的纸张增加一个直线维度后，相当于增加了厚度，变成立方体。
圆弧增加一个直线维度，会变成（空心的）圆柱面。站在这个圆柱面上，我们可以左右前后移动，当我们向前水平移动时，会回到起点，因为，这里有一个旋转的维度在里面。
螺旋线增加一个直线维度，会形成螺旋状的曲面。
2、增加旋转的维度
接下来看看旋转的维度对二维形状的改变。
一张纸卷曲起来，会形成圆柱面，这是二维平面变成三维曲线最简单的方式。因此，圆柱面既可以看作是平面卷曲的效果，也可以看作是圆弧沿直线拉伸的效果。
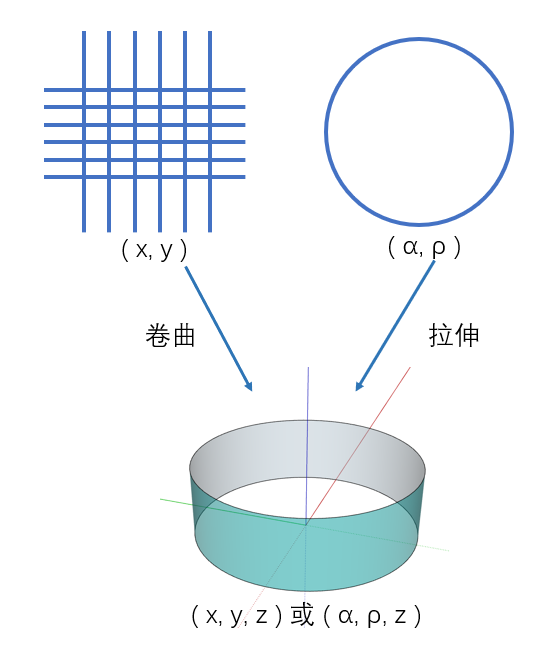
圆周在旋转时，有两种情况，一种是以圆心点为旋转中心，绕直径旋转一周得到球面。另一种情况是以圆外一点为旋转中心，旋转一周得到（空心）环状曲面。
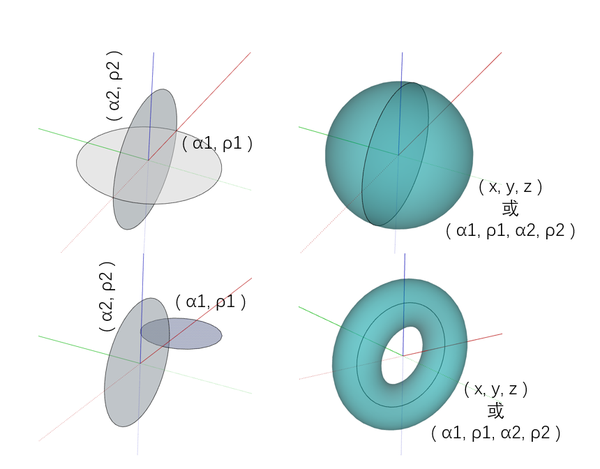
从上图可以看到，球面与环状面都通过增加一个旋转维度来实现的，它们属于同一维度的形状。
两个相垂直并相切的圆弧经过旋转，可以得到马鞍形状，其实它是上面提到的环状曲面的局部切片。
当平面在卷曲的过程中，伴随着的某一方向上的移动，会形成类似于扭曲的彩条形状。这种扭曲的条状与圆柱面属于相同的维度。
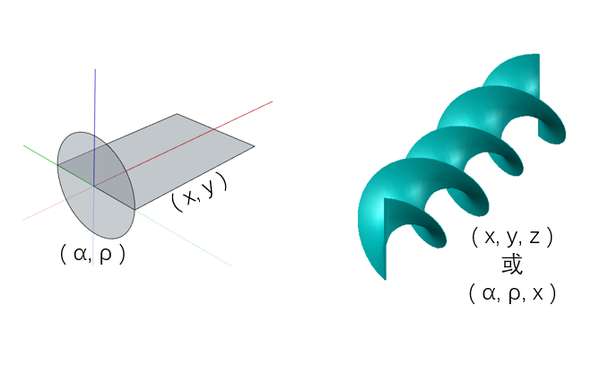
四维空间
若在前面提到的圆柱面、空心球面、扭曲的彩条面上增加垂直方向上的维度，圆柱面会变成实心，空心球会变成实心球。由于垂直方向上的维度可以将圆柱面变成无限“厚”，因此，理论上它将填满整个空间，与最简单的三维直线空间看起来完全一样。
这就好像大海深处某个位置有一个漩涡，只有处在其中时，可以感受到运动的方向不一样，从外面看，都是相同的实心水体。
上面提到的几种三维空间，增加“厚度”这个维度之后都将填满整个空间，不再是我们讨论的重点，我们继续关注增加旋转维度情况下的空间变化。
前面我们把圆柱面称为三维空间，在这个空间里增加直线维度—厚度，可以升级为四维。那么按照旋转的方式增加维度，会是什么样的效果？
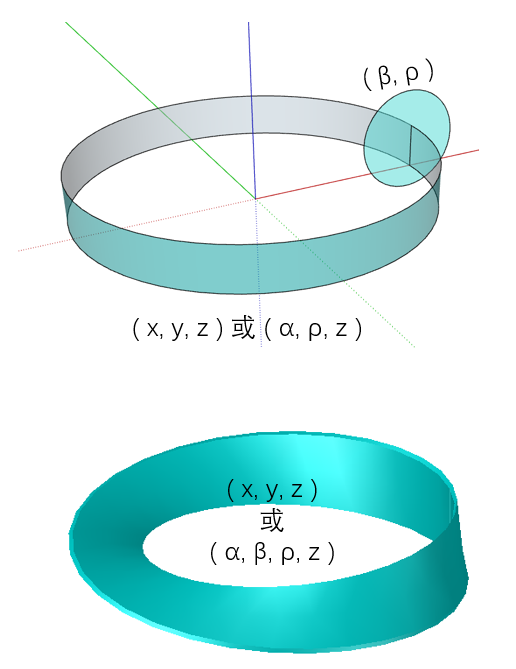
按照图中上方小圆方向对圆柱面进行扭曲，可以得到下方的图形。
圆柱面拆开旋转180°再接起来，得到一个很有名的形状——莫比乌斯环。
旋转的度数再增加一些，可以发现，每当增加180°的奇数倍时，圆柱面的正反面是相联通的，增加偶数倍时，正反面是不联通的。
使用CAD扫略命令（SWEEP），分别旋转多个180倍的度数，俯视图如下图所示：
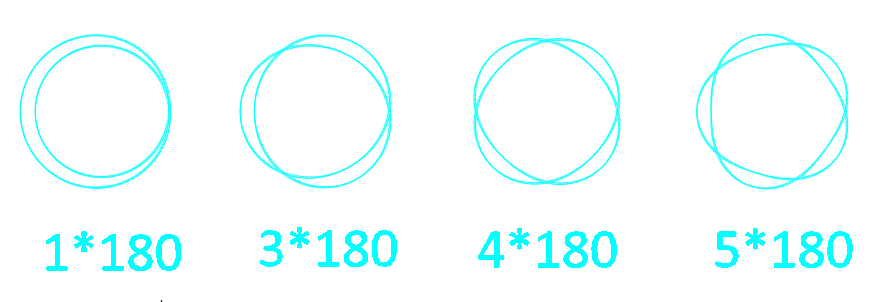
立体图如下图所示：
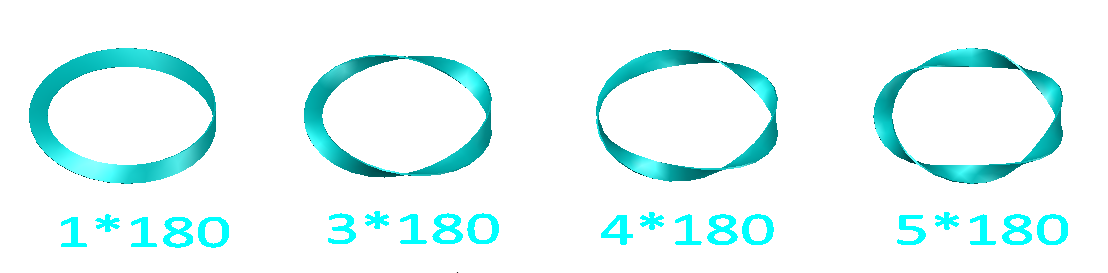
尽管这些曲面的旋转度数不同，但它们都在同一个旋转维度下连续变化得到的，所以它们属于同一个空间维度。如果旋转可以被定义为一个维度，则上面这些曲面都属于4维度的曲面。
五维空间
通过旋转增加维度时，空间没有被完全充满，于是维度就有了进一步升高的空间。
莫比乌斯带增加一个旋转的维度，就可以形成克莱茵瓶。刚想明白这个问题时激动了半天，上网一搜，别人早就证明了，连动画效果都有了（晚了一步哈）。这个话题就不多说了，总之，克莱茵瓶是属于五维度的空间。
通过旋转来扭曲空间时，并不总会像克莱茵瓶那样，形成封闭的空间曲面，发散的状态下，会像是螺旋线的多重叠加。
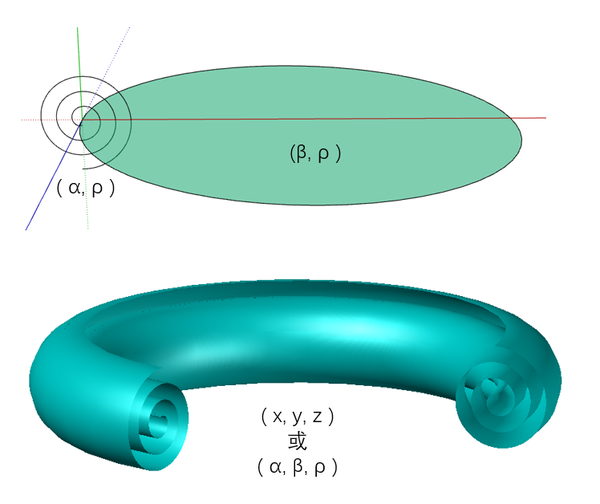
通过旋转增加维度时，旋转的方向会有多种的选择，所以会有多种的形状出现，很难画得完整，目前（我本人）的技术有限，就不再多画了。
六维空间
给克莱茵瓶增加一个垂直于表面的直线“厚度”维度，空间将再次被充满，所以六维度空间看起来会与三维度空间是相同的。
三维空间有三个直线轴向，在这三个直线轴向上分别叠加旋转的维度，刚好还是六维度的形式，大胆设想，对于复杂空间的数学定义可以是（x,y,z,α,β,γ）这样的坐标系来表示。后三者α,β,γ分别代表了以不同的圆心建立的坐标系，以角度来实现定位。
坐标系的应用举例
地球表面的位置点，我们可以用经纬度来表示，比如我国的大地原点，陕西省泾阳县永乐镇，位置在：北纬34°32′27.00″，东经108°55′25.00″。如果没有高度维度，我就会停留在这个（α,β）构成的二维地球表面。当人类能够离开地面，或是深入水中的时候，高度才有了意义，我们的空间就成为（α,β,z）构成的三维空间。
地球绕大阳旋转，本身又自转，在大阳系的维度中，地球表面上的点所经过的轨迹就像是多重旋转角度的莫比乌斯环。如果继续增加旋转中心点的定义，我们的维度还会有更多，但是精减合并下来，还是（x,y,z）就可以表达，只是公式上会复杂很多。
从直线到圆，只有增加额外的“引力”才能发生扭曲。若扭曲并不充分，就会有多种多样的曲线出现，很多的二次曲线、多次曲线，都可以看作是扭曲不充分，或是中间加入了新的“引力”原素，而形成的轨迹。总体来看，空间描述中六维度已经是客观描述的上限，或者说是可以图形表达出来的极限。更多的11维度、平行世界的想法，个人表示无法理解，只能呵呵了。
