聊一聊斐波那契螺旋
斐波那契螺旋（也称为黄金螺旋）是根据斐波那契数列得到的一种螺旋。
斐波那契数列是这样一种数列：1，1，2，3，5，8……，从第三项开始，每一项的数字是前两项数字之和。以这些数字为半径，连续绘制圆弧就可以得到如下面的斐波那契螺旋：
按照等距螺旋对螺旋的运动方式的解释，螺旋应由圆周运动与直线运动相叠加而产生，两种运动的速度比为固定值时，会形成等距离外扩的螺旋（简称等距螺旋，也称等速度比螺旋）。当速度比不固定时，螺旋会呈现出外扩幅度不断增大（或缩小）的特征。
斐波那契螺旋每一个旋转周期外扩的幅度都在增大，因此，它的速度比是在不断变化的。通过图形观察可以发现，斐波那契螺旋可以看作是基圆半径为1，扩张而成的螺旋。从半径为2的圆弧开始，可以找到下面的一组纯偶数数列：2，4，6，10，16，26……。
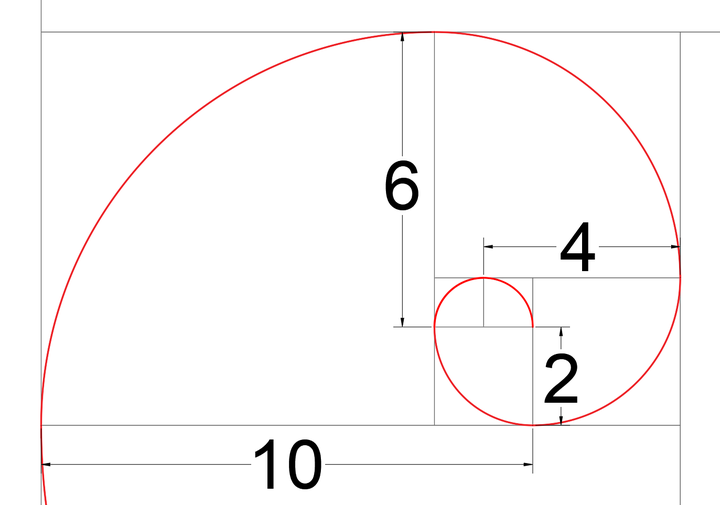
这组数列从第3项开始，每一项数字同样是前两项数字之和。百度“斐波那契数列”词条中有提到，类似的数列称为斐波那契—卢卡斯数列，所以这不是一项很特殊的发现。我们感兴趣的是直线运动与圆周运动在斐波那契螺旋中的具体体现和运动特点。
按照上面纯偶数数列在螺旋中的位置关系，我们可以发现，从圆弧半径2变化到4时，圆周旋转了90度，直线运动移动了2个单位；从4到6时，圆周旋转了90度，直线运动移动了2个单位；从6到10时，圆周旋转了90度，直线运动移动了4个单位。
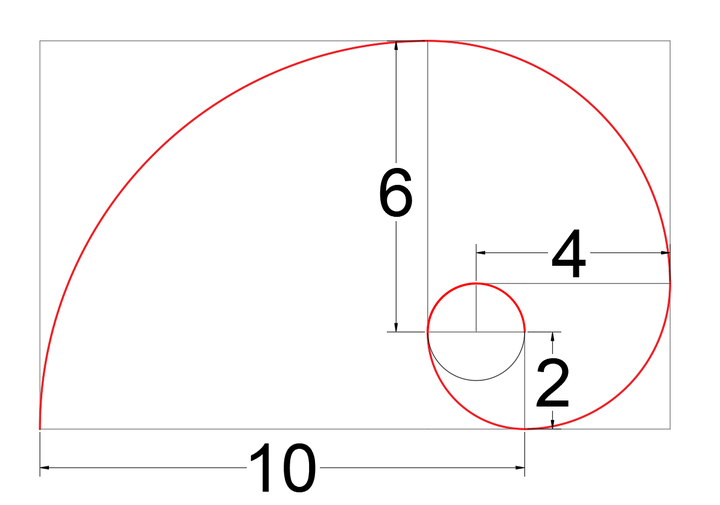
这样一个数列，实际上代表的是外圈螺旋与内圈螺旋之间的距离。如果将这个距离看作是直线运动的方向，那么，斐波那契螺旋中的直线运动是在逐渐远离圆心的。除了2，4，6这三项，直线距离圆心为1以外，此后的直线运动与圆心的距离每旋转90度，距离按照2，4，6，10的方式在增加。
再来看一下速度比的变化，从2到4，旋转90度，圆周速度用（2*Pi*r）/4来表示，r=1，则圆周速度为Pi/2。直线运动在这段时间内的距离值为2，所以直线运动与圆周运动的速度比为 2/(0.5*Pi)=4/Pi。其余位置的速度比用表格来表示：
区间 直线速度w 圆周速度v 速度比w/v
2~4 2 Pi/2 4/Pi
4~6 2 Pi/2 4/Pi
6~10 4 Pi/2 8/Pi
10~16 6 Pi/2 12/Pi
16~26 10 Pi/2 20/Pi
通过上表可以看到，斐波那契螺旋中的纯偶数数列可以看作是每旋转90度，所增加的直线方向上的距离，同时直线运动也是按照这样的数列在远离圆心。我们假定每旋转90度时，圆周运动的速度保持不变，则斐波那契螺旋中的速度比是按照4，4，8，12，20的数列在增加，符合我们对于“非等距螺旋是由于速度比在增加而产生的”这样的一种判断。
此外，螺旋每旋转90度，直线运动上增加整数距离，而90度弧长一定对应Pi/2的倍数，二者无法精确相等，因此，斐波那契螺旋并不是基于自身展开的渐开线。
外圈的斐波那契螺旋的直线运动总是与内圈的旋转相切，位置关系如下图所示：
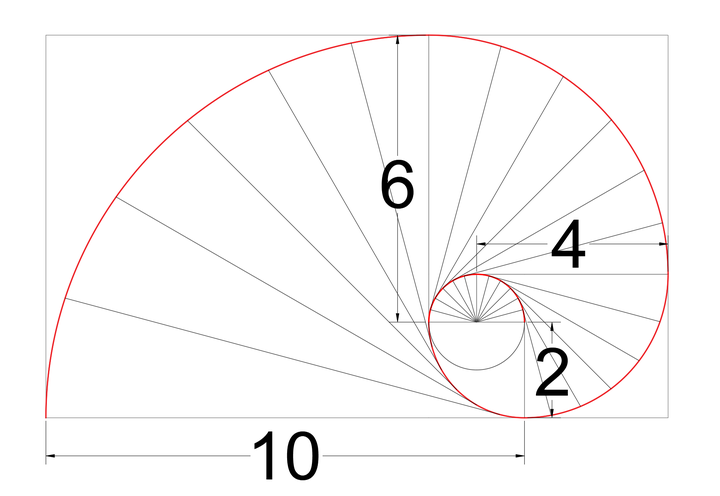
从上图可以看到，斐波那契螺旋具有自相似特性，每一个外圈的螺旋都与内侧的那一层螺旋相关。用直线运动与圆周运动来解释，那就是直线运动一直在按照2，4，6，10这样的数列扩散。在这个过程中，速度比一直在不断增加。
螺旋从大的范围来看是能够找到对称图形的，对于斐波那契螺旋来说，每一段圆弧的端点都可以作为一个对称点来使用。如果从基圆开始做对称螺旋，会是下面的形状：
从上图可以知道，螺旋的对称性对于斐波那契螺旋是同样适用的。那么螺旋的互补性呢？
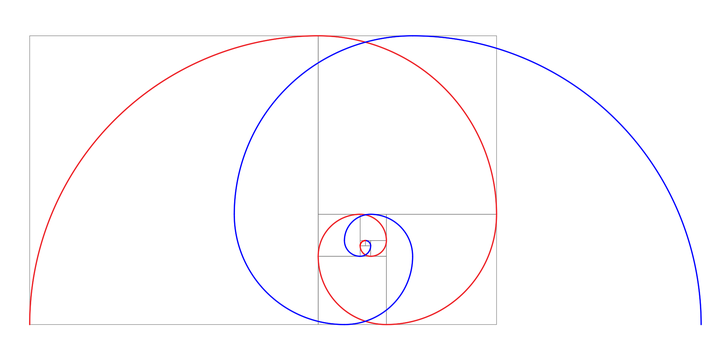
从形态上来看，斐波那契螺旋与下图中的蓝色曲线非常的相似，那么它的互补螺旋必将与红色部分的螺旋相近。（如果将蓝色螺旋看做是逆时针旋转所产生的螺旋，那么红色螺旋则是顺时针旋转所产生的螺旋，这两条螺旋称为互补螺旋）
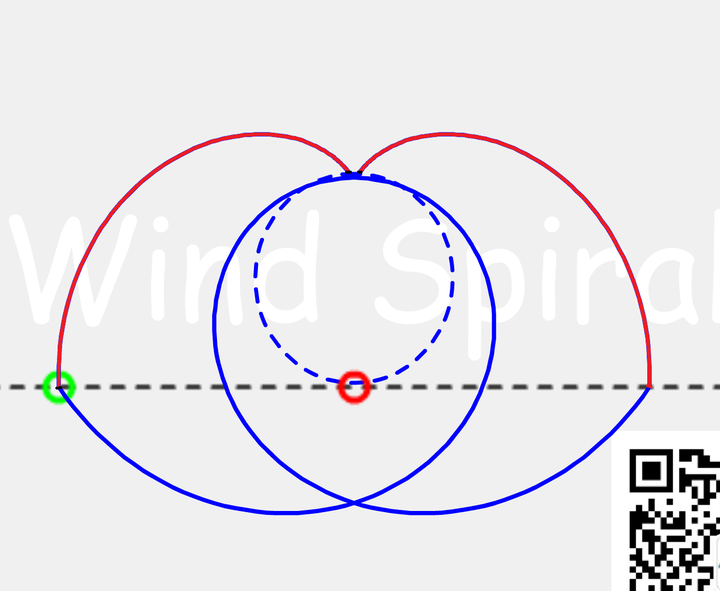
由于上图是在等距螺旋的框架下绘制的螺旋，因此，并不能精确体现出斐波那契螺旋的位置关系。斐波那契螺旋与等距螺旋的差别主要有两点，一是速度比一直在变化，不是固定值。二是直线运动逐渐远离圆心，位置不是固定不变的。
以我的数学基础目前解决不了螺旋公式构建的问题，留给感兴趣的人来分析吧，或者将来有时间了，再来详细讨论一下，从非等距螺旋的角度来构建斐波那契螺旋的参数公式。
目前来看，圆弧的表示方法相当于粗颗粒度（低精度）的螺旋画法，斐波那契螺旋一定可以用更精确的数学公式来进行描述，而这个公式在每一个90度位置计算的结果都应该是一个整数。这将是打通无理数与有理数之间关系的一种计算方法，或许还会对我们的数学观念带来一些改变，一切皆有可能，你怎么看呢？
外面正是病毒肆虐的时候，宅在家里也是对社会的贡献。有句话说的好，永远也不知道明天和意外究竟那一个会先到，那么我们唯一可以把握的就是当下。努力过好每一天，不虚度时光，喜欢的事情就全力以付去完成，每多走一步，就有一步的成长，每多思考一点，就有一点的收获，如此，甚好。
祝大家百毒不侵，平安喜乐~~
