复联四中的莫比乌斯环究竟是几维的？

 

复联四中有一个情节，钢铁侠拒绝了队友的求助，而后在内心的驱使下，对着一个立体的莫比乌斯环，自行验证时空穿越的可能性，最后实验成功，一切重启。

时空穿越现阶段只在电影里有可能，而莫比乌斯环的维度问题，我们现在就可以来聊一聊。

 

 

某度中对莫比乌斯带的解释如下：

它是由德国数学家、天文学家莫比乌斯（August Ferdinand Möbius）和约翰·李斯丁（Johhan Benedict Listing）在1858年独立发现的。这个结构可以用一个纸带旋转半圈再把两端粘上之后轻而易举地制作出来。事实上有两种不同的莫比乌斯带镜像，他们相互对称。如果把纸带顺时针旋转再粘贴，就会形成一个右手性的莫比乌斯带，反之亦类似。

 

 

当物体沿着莫比乌斯带的中线移动时，就会发现可以从纸张的正面平滑的移动到纸张的背面，看起来，这两个面似乎是在同一个平面里，维度相当于零，这样的认识究竟错在哪里了呢？

首先，按照现有“维度”的定义，一个具体的纸带它一定是三维的，用长、宽、高来表示，但这样的三维设定无法解释两个面之间为什么会平滑连接，因为，在现有的“维度”定义中没有将旋转视为一个维度。

地球是旋转的、太阳系是旋转的、宇宙应该也是在旋转的，而我们一直没有把旋转看做是一个维度。

一个纸条可以看成是长和宽构成的二维平面，如果只是直线方向上增加维度，它始终变不成曲面，而通过增加一个水平的旋转维度，一张纸条就可以变成一个柱面形状。

 

 

如果再将这个圆柱面切开，接口处旋转180度，重新接上，就可以得到莫比乌斯环。在这样的操作中，在圆柱面的垂直方向上又增加了一个旋转的维度，旋转方向与下图所示。

 

 

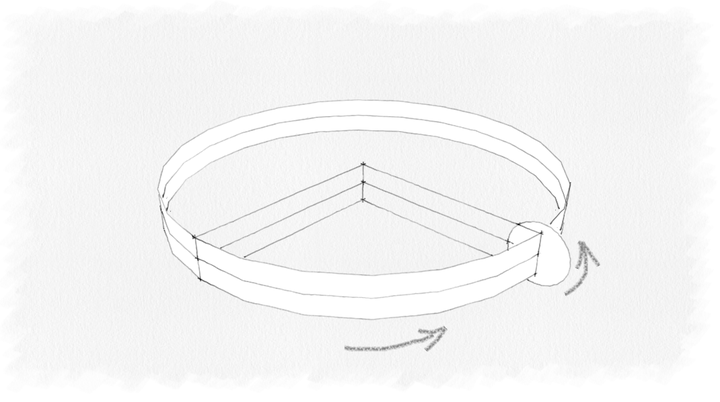
从这样的角度来看，莫比乌斯带实际上是二维平面增加了两个旋转维度之后的产物。两个旋转的维度互相垂直，不可以互相替代，因此，莫比乌斯带是带有两个旋转维度的四维空间。

圆柱侧面上如果继续增加旋转的度数，它的变化是连续的，并且可以用圆柱面的维度参数来进行描述，因此，并不会导至维度的继续增加。

圆柱面上的旋转可以有两种方向（正旋和反旋），会形成两种不同的莫比乌斯带，从维度上来说它们是相同的四维空间，只是旋转的方向有差别。

直线运动与圆周的旋转运动相叠加，可以产生螺旋状曲线。直线可以看做是一维空间，那么螺旋线则是二维空间。从数学公式上可以知道，当直线上的速度为零时，按照圆周进行运动的动点可以画出一个圆来，因此，从运动的角度来看，圆是一个纯粹的一维旋转的空间。

慧星从天际滑过，在我们眼中，它划出了一条直线，而地球的旋转我们感觉不到，二者在空间中的叠加轨迹恰好是一种螺旋状的轨迹。

与莫比乌斯环最相似的空间环境应该是洗衣机内的水流。整体绕着中心轴在旋转，旋转的过程中水流受机体结构的影响，上下翻转着。如果能把这些水流切成带状，那么一定是莫比乌斯带的形状。

因为有了旋转的维度，太阳每天都从东方升起，终点可以变成起点，世界有着无限连通的可能性，是否宇宙就是按照衣机模式在运行着呢？每一个星系就是一个流动的旋涡，每一个星球就是这旋涡中的一粒尘埃。