基于数学软件的阿基米德螺线切线计算与分析
要：通过运用数学软件，按照中学课程中导数求解的思路，简便实现阿基米德螺线切线的计算，并对验证结果进行分析得出结论，为拓展中学数学教学方法提供参考。
关键词：阿基米德螺线 导数 数学教学 Mathematica 交互
Calculate and Demonstrate of Tangent Line for Archimedean Sprial
Abstract：To simplify the calculate and demonstrate of tangent line for Archimedean spiral in middle school teaching, it will be achieved by using the mathmatic software. Following the step of derivative method, the conclusion could be got and observed easily. The method discussed in the article could be widly adopted for math teaching in middle school.
Key words：Archimedes’ Sprial
引言
高中数学中的导数部分一直是教学中的难点，提高教学内容的直观性和趣味性、开发适合中学生操作的实验课题，对于增加课堂吸引力和提高学生理解力将大有帮助。通过引入成熟的数学软件，将公式推导的过程进行简化，可以有效帮助学生理解导数的概念和应用，从而为大学的学习奠定良好的数学基础，同时为课堂教学提供更新颖的方式和方法。下面以阿基米德螺线的切线求解为例来分析导数概念在曲线求解中的应用。
1 阿基米德螺线的描述与公式
阿基米德螺线是古希腊数学家阿基米德提出的一种螺旋曲线，它的描述形式为：一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹。阿基米德螺线简化后的极坐标方程式为：r = a *θ
其中r表示的是动点距圆心的距离，a表示的是每旋转周期内，动点移动过的距离，θ表示射线旋转过的角度。
想要得到指定θ角度的切线方程，分析多个周期间切线的位置关系，这样的问题就属于典型的极坐标曲线求切线的问题，通过导数的计算方法可以简单的加以实现。
2 极坐标曲线切线计算的步骤和方法
极坐标曲线的切线计算可以按照下面的步骤来进行：
1.将极坐标公式转换为直角坐标系公式。
2.分别对x(θ)、y(θ)函数进行求导，得到x'(θ) 、y' (θ)，二者相除可以得到切线的斜率公式。
3.按照指定的角度θ0代入直角坐标公式和斜率公式组成切线方程。
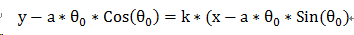
函数求导和切线方程的建立是整个计算中的难点，随着曲线函数复杂度的提高，手工推导的难度将大大增加，不利于对整体概念的理解和掌握。曲线与切线的关系展示也是传统教学中的难点，很难动态的去改变参数并展示结果。通过引入数学软件，以上问题都可以很好的得到解决。
3 Mathematica软件的基本用法
Mathematica是一款非常专业的科学计算软件，具有非常强大的数值和符号计算功能，它与MATLAB和Maple 并称为三大数学软件。Mathematica软件简便易用，它的书写形式更接近于自然语言，适合进行复杂的数学公式推导与验证。
在Mathematica中对公式求导是通过D[ ]函数来实现[1]，以阿基米德螺线切线斜率的计算为例，通过以下的代码即可实现斜率公式的推导：
运行以上代码可以得到斜率及切线的公式：
直线的显示可以用Plot[ ]函数，例如绘制直线y=5x+3，x在[-10,10]区间内的线段：
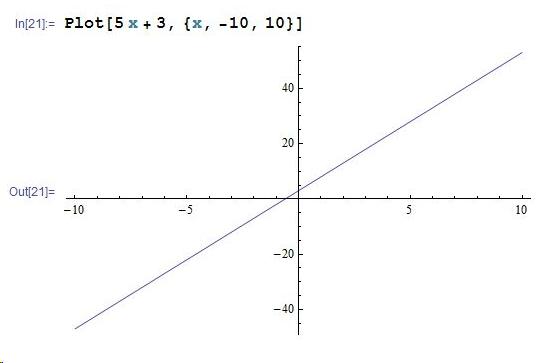
曲线的显示使用ParametricPlot[ ]函数来实现，比如绘制从0度至6Pi的阿基米德累线：
从上图中可以看到，Mathematica中的坐标系和日常教学中的坐标系是完全一致的，角度是按逆时针方向增长，函数中的角度值均按弧度值来取值。上图中还可以看到公式中a的取值在坐标轴上的体现，由于在x轴正方向上，每旋转一周，动点移动2*Pi*a的距离，若将a取值为50/Pi，则曲线与正向x坐标轴的交点是100的整数倍。
在切线公式代码的基础上，添加以下代码进行数据测试：
Mathematica软件会将运行过的计算公式保存在内存中，对变量直接赋值，直接引用公式项，如上图中的k项和t项，则可以输出计算结果。将绘图函数的结果保存到一个变量中，比如上图中的f1，函数末尾用分号结束，表示当前运算结果暂不输出，最后统一用Show[ ]函数将图形结果叠加在一起一并输出。通过以上代码，最终实现交替输出斜率与切线公式，之后合并输出曲线与切线的图形：
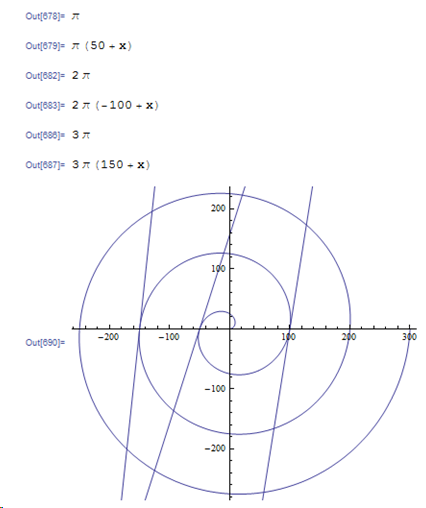
为了避免前次运算的结果对后续运算造成干扰，在代码开前用Clear[ ]函数对所有变量进行清零是一个较好的编程习惯。
4 计算结果的分析
通过设定不同的θ角度值，执行代码，可以看到不同的运算结果。
θ角度值为零时，切线与x轴重合，这符合动点运动方向的初始设定，即动点从原点开始向x轴正方向匀速移动，同时按照逆时针方向（角度增大的方向）旋转，最后形成阿基米德螺线的轨迹。
在以上的实验中，θ角按照Pi为间隔进行测试，斜率k的值“恰好”等于θ角度值。若以Pi/2为间隔，可以得到更具普遍性的结论：k值的变化不是均匀的，与θ值没有直接的对等关系，k值的正负值变化能很好的说明这一点。
在阿基米德《论螺线》的命题18，19中提到，当旋转完一个完整周期时（θ=2Pi），绘制的切线与y轴的交点距原点的距离等于以动点到圆心距离为半径的圆弧的周长。并且以后每个完整周期都符合这个规律。
按照实验中的参数来看，第一圈的半径等于100，圆周长为200Pi，与y轴的交点为（0，-200Pi），距离原点距离符合命题中的结论。x轴方向距离成倍增加时，y轴负方向距离也成倍增加，因此证明命题18，19是准确的。
若θ角度值不是2Pi的整数倍，则可以很容易的发现命题18，19中的规律是不适用的。比如当θ角度为3Pi时，实验中的切线公式为y= 3Pi(150+x)，很显然（x轴距离的2Pi倍）150*2Pi不等于（y轴距离）3Pi*150。因此，《论螺线》的命题18，19仅适用于θ角度值为2Pi整数倍的情况。
通过间隔为2Pi的切线斜率可以看到，每增加一个周期，斜率也会同步增加，因此，各条切线之间是不平行的，因此在大多数情况下x轴与y轴交点间的距离没有固定的比例关系。
5 结束语
通过使用数学软件，合理设计实验题目，可以简便快捷的将计算原理与图形效果紧密结合起来，帮助学生克服公式推导中的困难，从而更深入的从原理和结果之间的关系入手，进行分析和掌握课堂知识点。对于教学人员而言，应积极主动的了解和掌握新的软件应用方法，达到丰富教学手段，增强教学效果的目的。
参考文献：
[1] 章美月,刘海媛,金花. Mathematica数学软件与数学实验[M].徐州:中国矿业大学出版社，2013.
///辅导过的一篇论文，刊发时把图片都丢了，所以在这里补发一下。
