【等距螺旋的七个实验】实验三：认识风螺旋
若将螺旋看做是直线运动与圆周运动的叠加，每个旋转周期，直线上移动相同的距离，这样得到的螺旋曲线可以统称为等距螺旋。
【风螺旋的由来】
风螺旋是国际民航组织DOC8168规范中提到的，在飞行程序设计中使用的一种螺旋状曲线，用来描述航空器转弯过程中受风的影响而形成的最大的转弯外边界。
按照等距螺旋的运动形式进行分析，可以发现，风螺旋是直线运动与圆周运动相交的情况下，所产生的一种螺旋曲线。
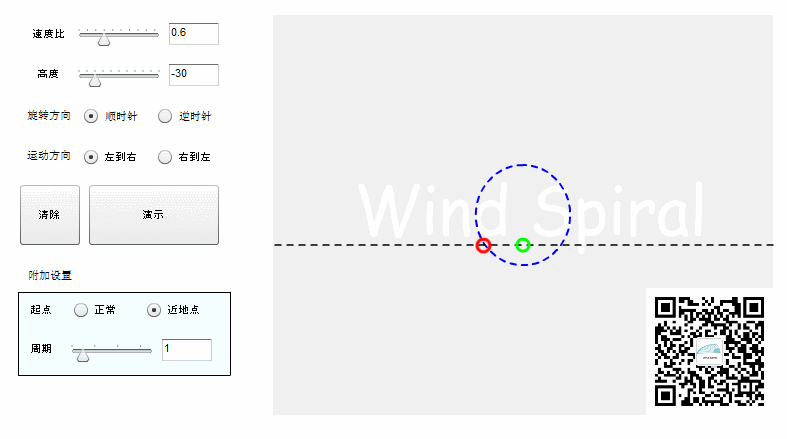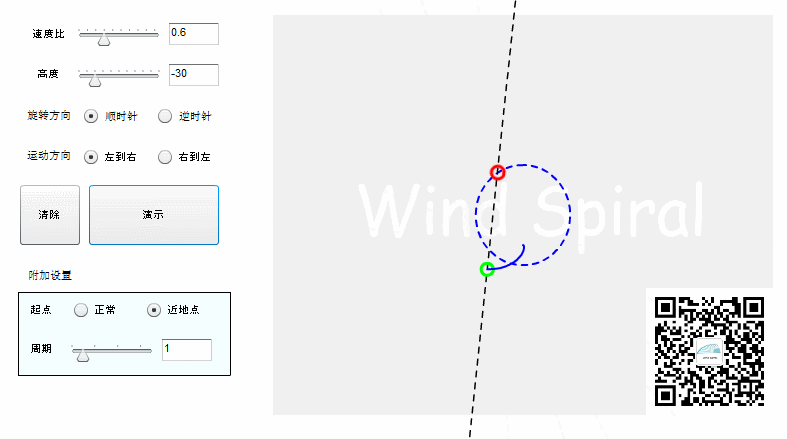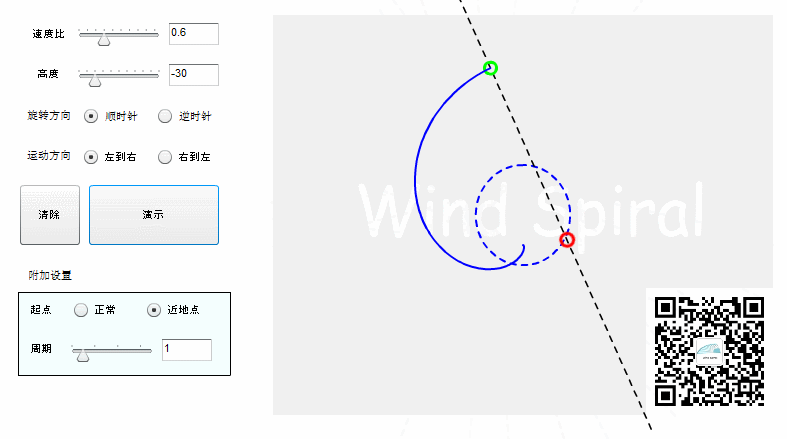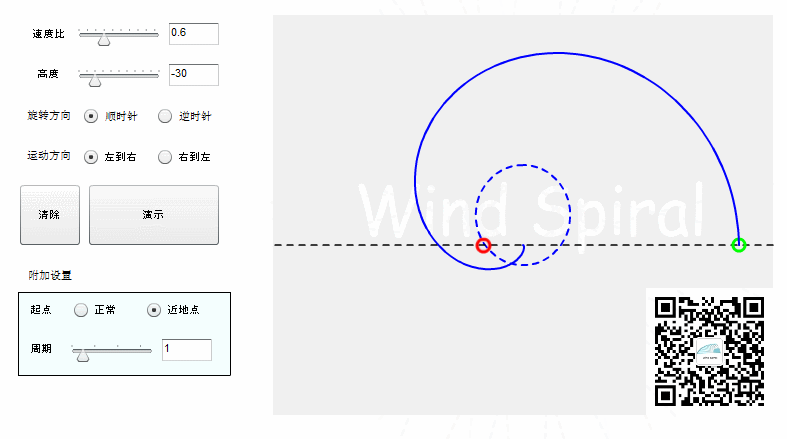
图1. 风螺旋线
（注：飞行程序设计中仅使用风螺旋在圆周以外的部分。）
若将圆周运动的速度用v来表示，直线运动的速度用w来表示，直线距圆心的距离用D来表示，圆周的半径用r来表示，那么风螺旋对速度的要求是:
w/v = D/r
图1中 w/v等于0.6 ,圆的半径为50,故D(高度)为30。
【对称特性】
顺时针外扩的螺旋与逆时针外扩的螺旋，可以构成一条完整的螺旋曲线。风螺旋也不例外，“完整”的风螺旋是下面的样子：
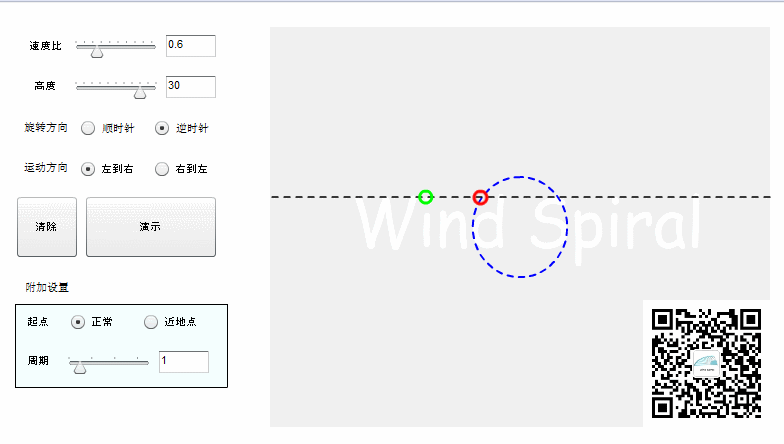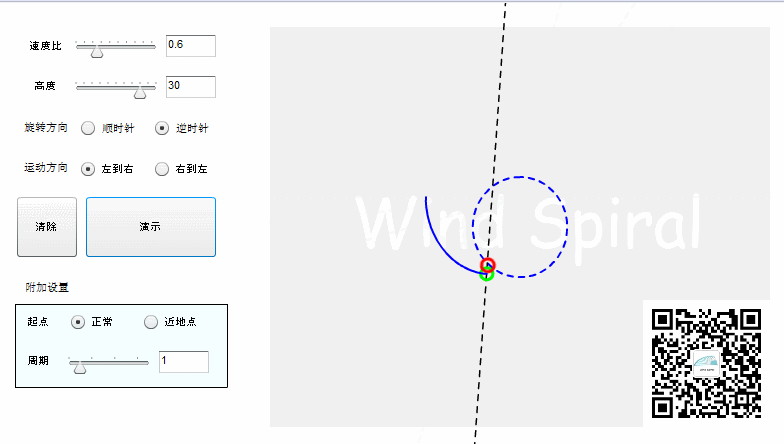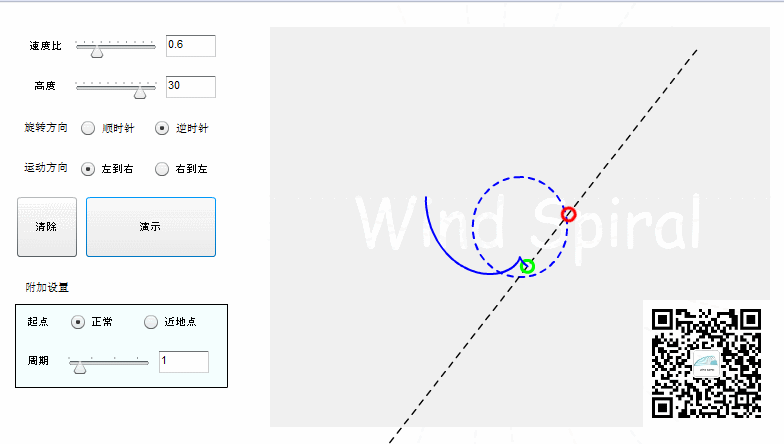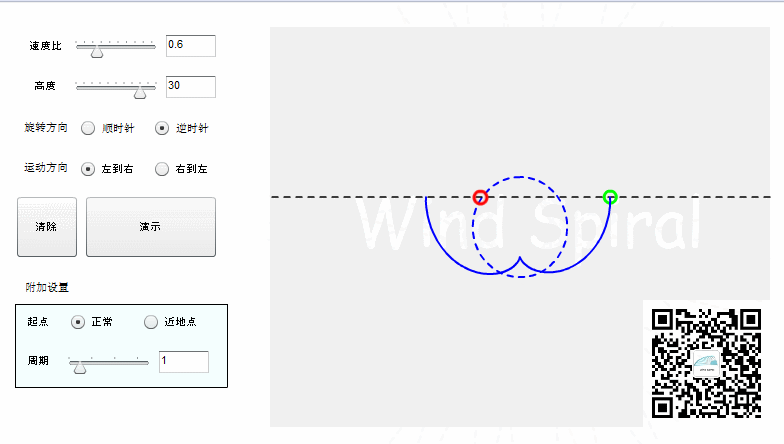
图2. 完整的风螺旋
从上面的图形可以看到，直线运动与圆周运动相交，同样可以产生出对称的螺旋状曲线，对称轴在图2中是过圆心与初始位置的直线相垂直的直径。
风螺旋的位置关系更具普遍性，它恰好是介于渐开线与阿基米德螺旋之间的一种形态，但风螺旋的数学定义更为严格，对运动的方向也有特定的要求。
【互补特性】
当圆周运动的旋转方向改变时，同样的直线运动可以产生不同的螺旋轨迹，这样的两种轨迹在对称轴的位置精确相切，形成互补的两条螺旋。
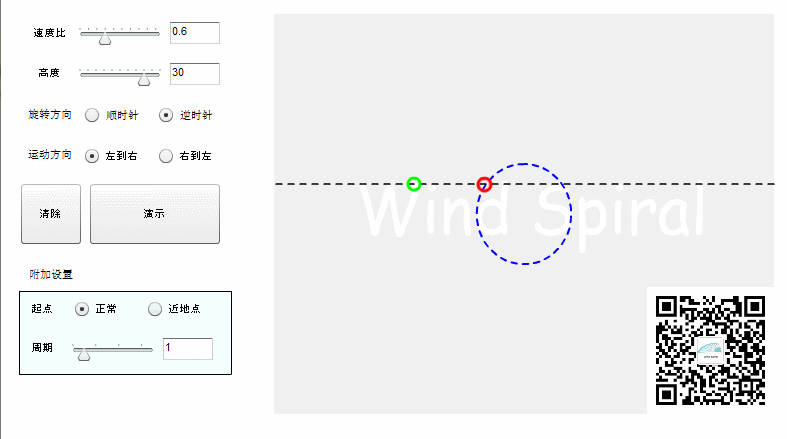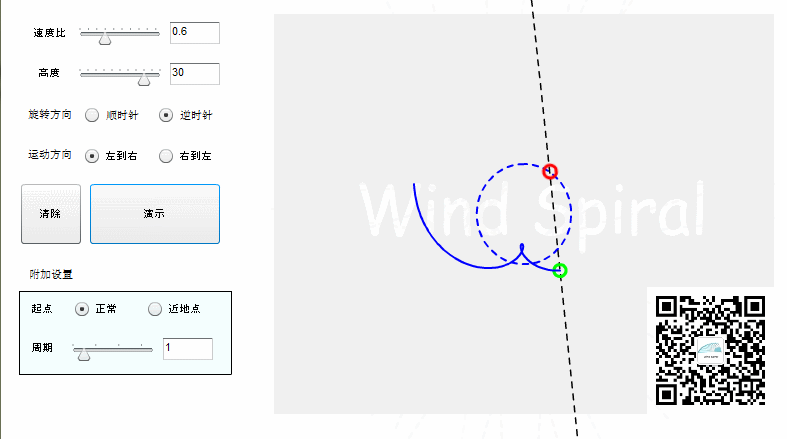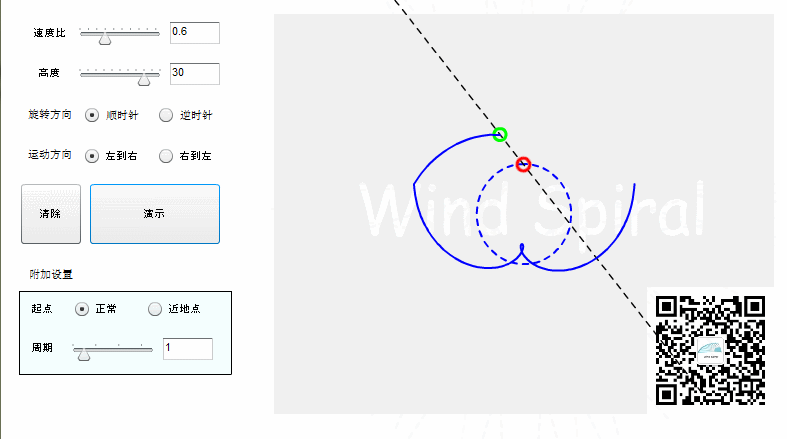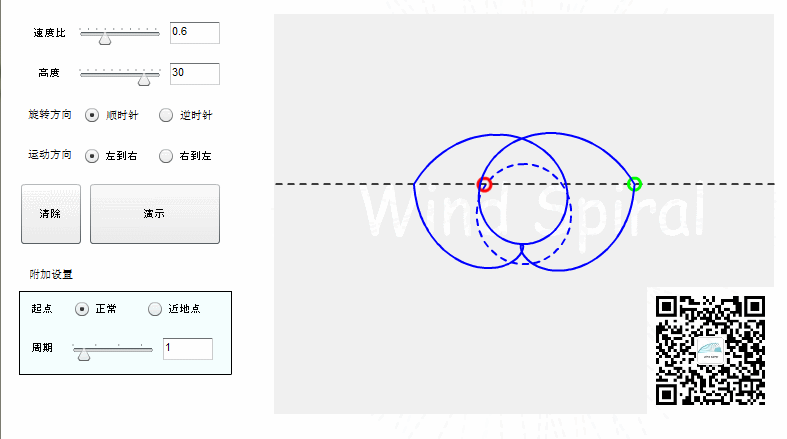
图3. 互补的风螺旋
由于互补出来的螺旋的形态及数学特征与风螺旋已经完全不一样了，因此，风螺旋的互补螺旋不能再称为风螺旋。
渐开线螺旋的互补螺旋同样也不能再被视为渐开线。
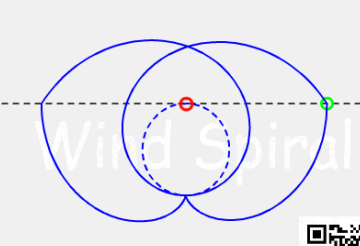
图4. 互补的渐开线螺旋
阿基米德螺旋由于它特殊的圆心位置，所以它的互补螺旋仍是阿基米德螺旋，并且样子完全相同。
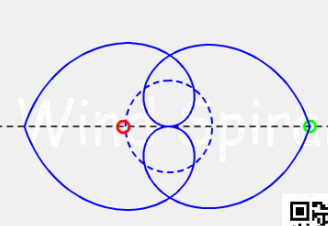
图5. 互补的阿基米德螺旋
【公式分析】
风螺旋中的角度关系如下图所示：
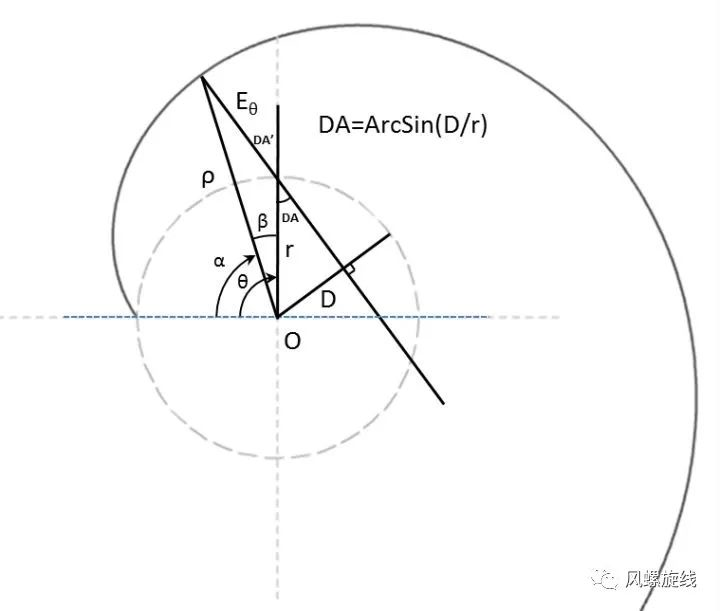
另一个方向的角度关系如下图所示：
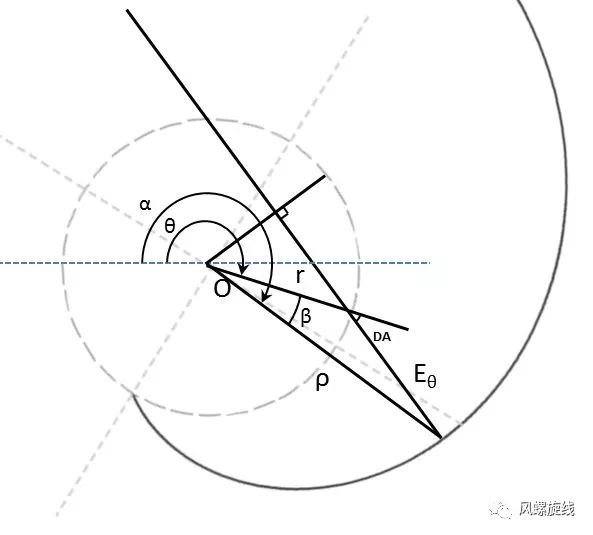
以上两种角度关系按照余弦定理进行推导，分别对应下面的公式二与公式三：
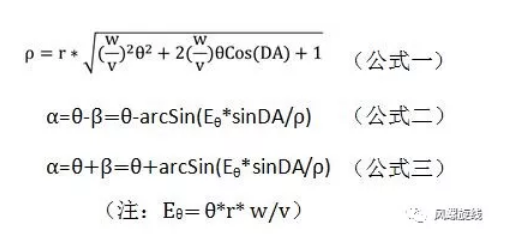
飞行程序设计中所采用的风螺旋，包含的计算条件有：直线运动的速度w不大于圆周运动的速度v，运动方向相逆（夹角大于90°），二者的速度之比等于直线距圆心的距离D与圆周半径r之比。若用DA来表示两种运动之间的夹角，则sinDA=w/v=D/r 。
风螺旋的公式中，w与v并不单独出现，而是以“比值”的形式存在。也就是说螺旋线的形态与速度比有关，与是否是匀速直线运动无关。若直线速度与圆周速度同时增大两倍，由于速度比不变，所以螺旋的形状也不会变。
阿基米德螺旋对速度比无特定要求，但要求直线必须过圆心。从公式来看，当DA角为零度时，直线过圆心，公式可以化简为：
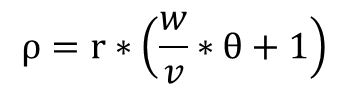
与常规的阿基米德螺旋极坐标公式 ρ=a*𝝷 是一致的。由于阿基米德螺旋公式是一种简化后的公式，缺少等距螺旋公式中的一些必要条件，也因此，无法向渐开线公式进行转换。
渐开线螺旋的公式可以由风螺旋公式转化得到，当DA等于90°，w/v等于1时，可以形成渐开线。由于渐开线 速度比 与角度的关系符合风螺旋的参数条件，因此，渐开线可以看作是风螺旋的一个特例。
由于风螺旋对速度比与角度有特定的要求，因此，对于一个指定的直线与圆周相交的位置，风螺旋有且仅有一条。
风螺旋的公式可以转化为阿基米德螺旋公式与渐开线公式，因此，风螺旋公式是等距螺旋的通用公式。
【切线特性】
阿基米德螺旋的切线方向是不固定的，因此看起来杂乱无章：
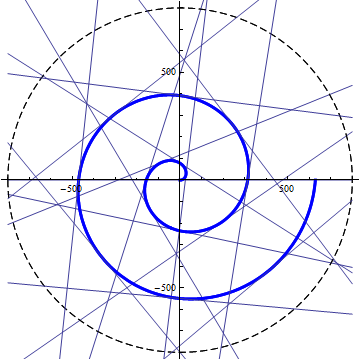
图6. 阿基米德螺旋与间隔45°的切线
渐开线螺旋的切线与运动方向相垂直，因此非常的规整：
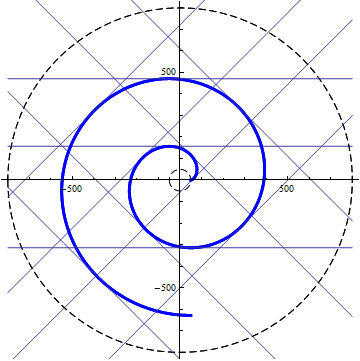
图7. 间隔45°的渐开线切线
风螺旋在基圆以外部分的切线与渐开线是一致的，（渐开线是风螺旋的特例），间隔180度的切线之间互相平行，如下图所示：
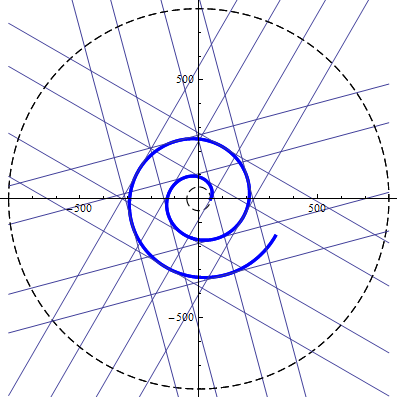
图8. 风螺旋与它的切线
渐开线并不会延伸到基圆以内，而风螺旋与圆相交，它会延伸到基圆以内，基圆以内的切线方向变化较大，与外部的切线特性不同。
风螺旋在应用时，是按照w小于v来考虑的，当w大于v时，又会是什么样的情况呢，留到下次再来讨论。
【软件下载】
等距螺旋实验演示软件：
https://pan.baidu.com/s/1d7KeVKclptXuvuGI5XMFBA
扩展阅读
【等距螺旋的七个实验】实验一 阿基米德螺旋的再认识
