【等距螺旋的七个实验】实验一

实验一：从射线到直线，阿基米德螺旋的再认识

【等距螺旋的七个实验】

　　若将螺旋看做是直线运动与圆周运动的叠加，每个旋转周期，直线上移动相同的距离，这样得到的螺旋曲线可以统称为等距螺旋。

　　当直线穿过圆心时，形成的螺旋即为阿基米德螺旋。

【运动形式】

　　传统的阿基米德螺旋描述了动点从一个原点出发，沿直线运动，同时直线绕原点旋转时，动点所形成的轨迹。

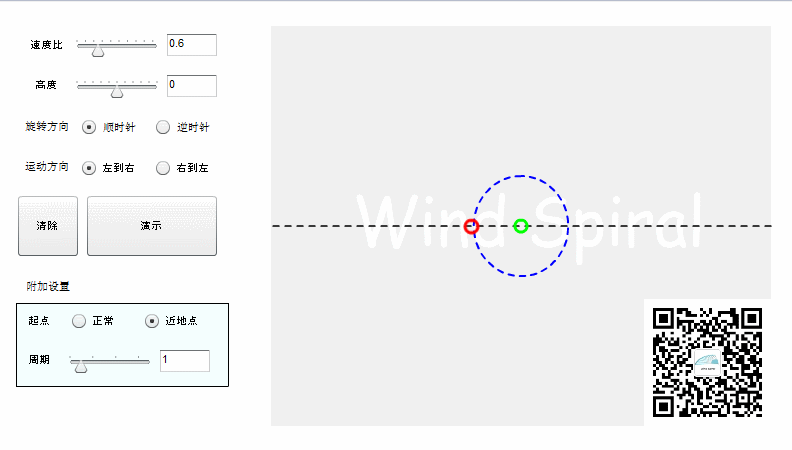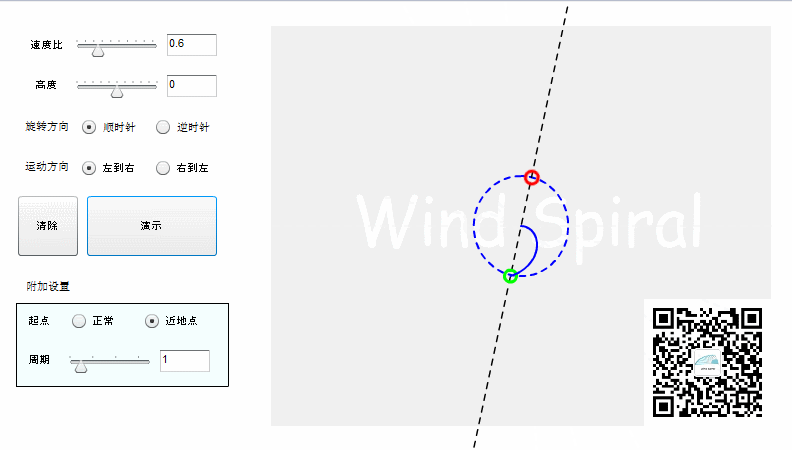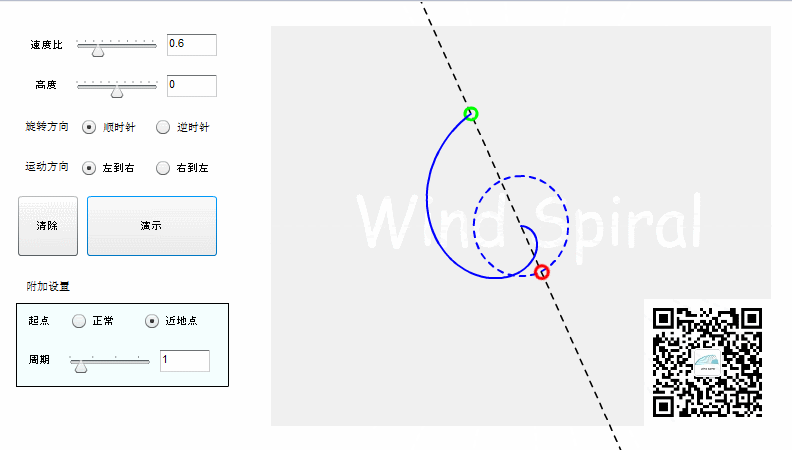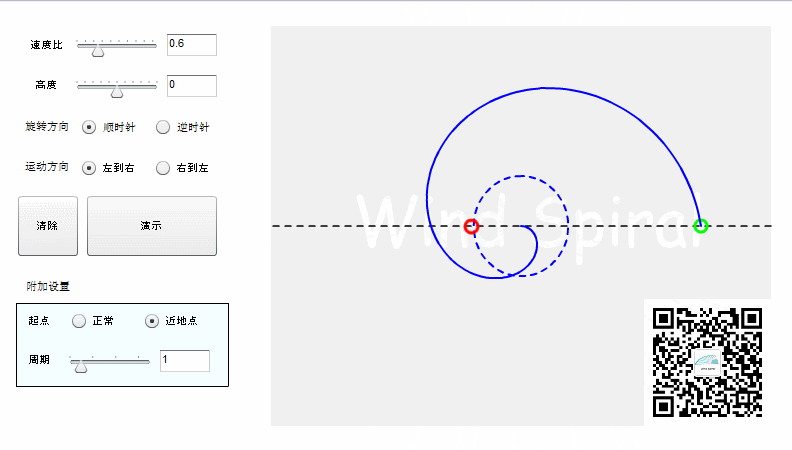
　　实际上阿基米德螺旋并不是完整的直线运动，而是射线运动。如果按照直线运动的方式来记录轨迹，则可以得到下面的结果。

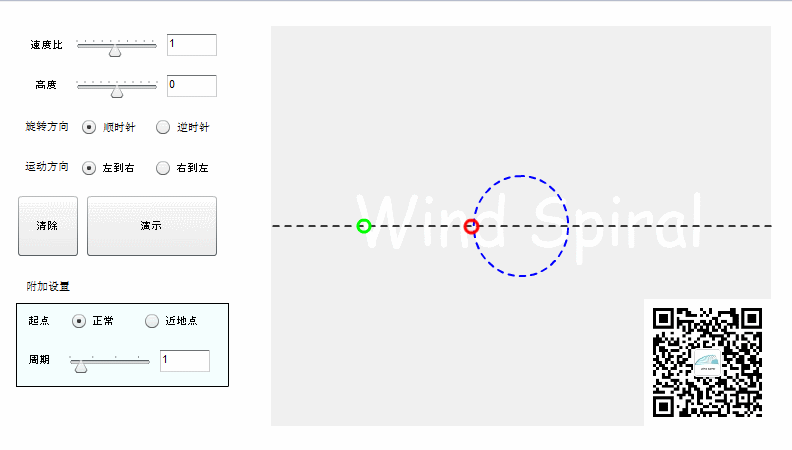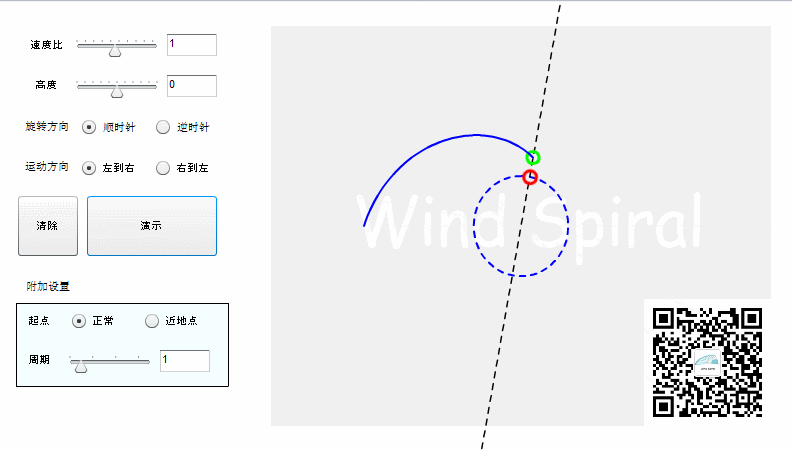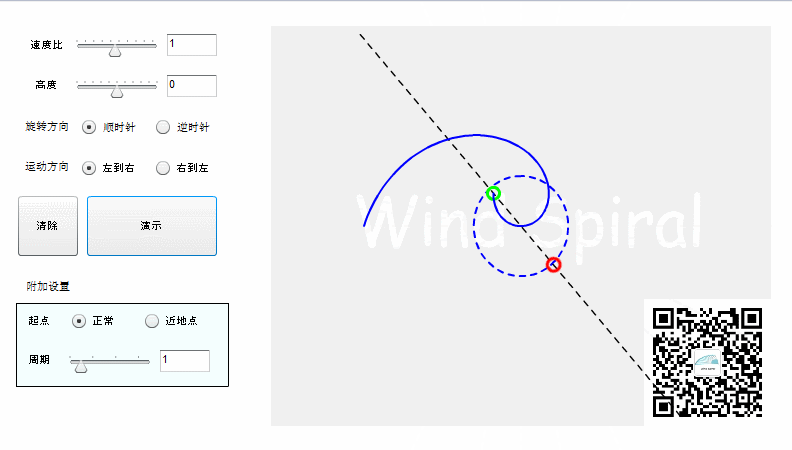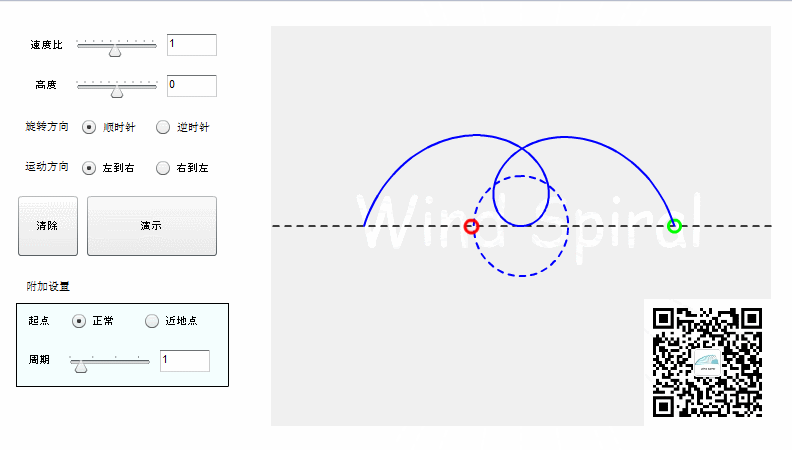
　　旋转可以分为顺时针与逆时针，对于同样的直线运动，不同的旋转方向所产生的轨迹将是下面的情况。

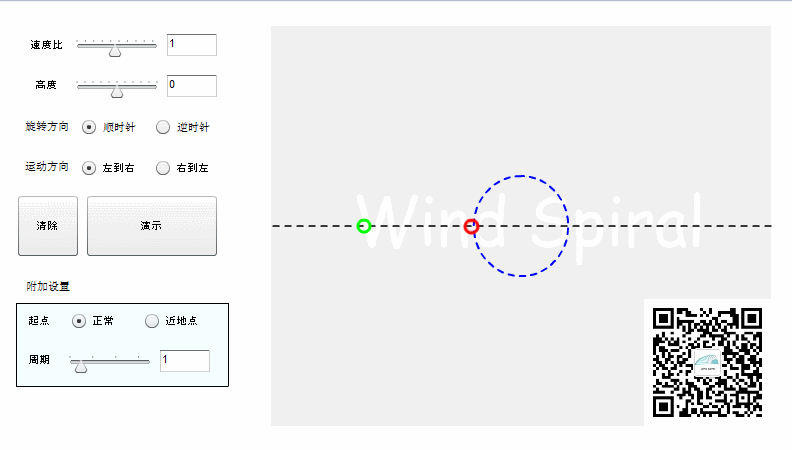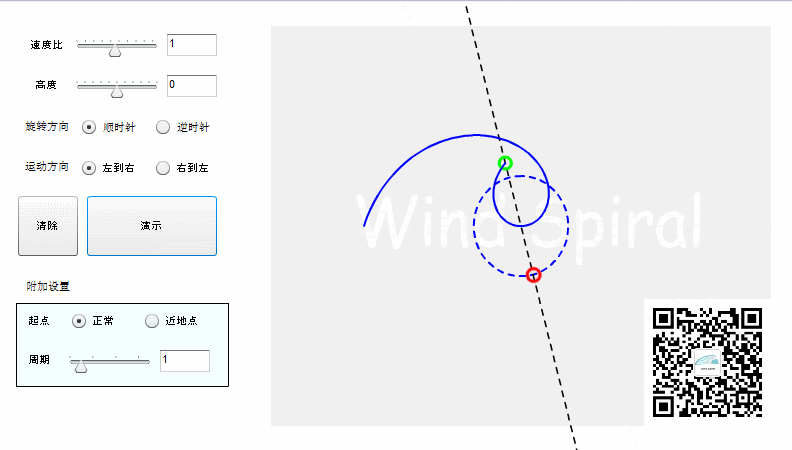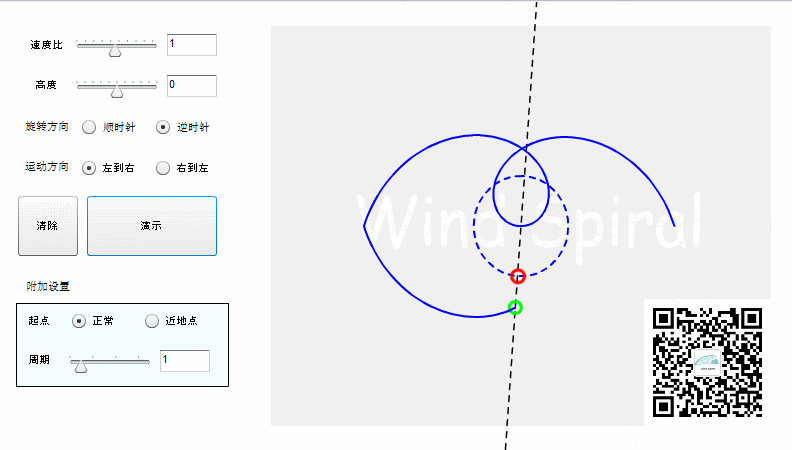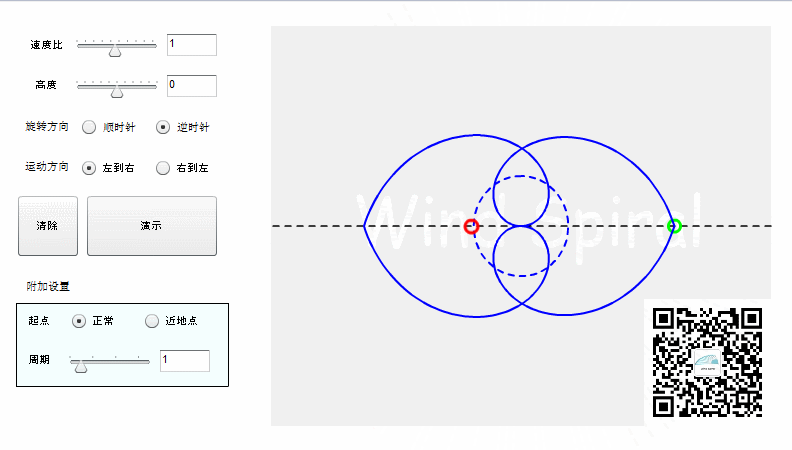
【对称特性】

　　从上面的图形可以看到，阿基米德螺旋顺时针旋转、逆时针旋转所形成的轨迹是完全对称的，这是阿基米德螺旋所特有的对称特性。如果直线运动改为从右向左，得到的轨迹仍然是与上图相同。

 

【公式分析】

　　阿基米德的一般公式为：　 ，该公式中未能体现出运动速度的变化对曲线的影响。传统的理解：认为匀速直线运动与匀速圆周运动相结合，可以得到阿基米德螺旋。

　　实际上当直线速度与圆周速度 统一增大一倍时，螺旋的形状是完全相同的。因此，等速螺旋的称法是不恰当的，对于等距螺旋来说，用等速度比来形容更为恰当。后面的实验中，我们将揭晓等距螺旋的通用公式，从公式中将可以看到引入速度比的情况下，能够更加准确的对等距螺旋进行描述。

　　　　　　　　　　======以下属于主观臆测部分======

　　“从哪里来，到哪里去”永远是哲学世界里一个难以回答的问题。在等距螺旋的世界里，这个问题比较好回答，我们从哪里来，就将回到哪里去。每一个旋转周期中，顺时针外扩的螺旋、都会与逆进针外扩的螺旋相交，而它们可以是同一种运动形式下连续形成的轨迹。如果我们是从无限远的某个地方沿着螺旋轨迹而来，那么也必将沿着螺旋轨迹回到那个无限远的地方（前提条件是生命的跨度足够的长）。

　　《金刚经》中提到“如来者，无所从来，亦无所去，故名如来”。如果我们站在螺旋轨迹上的一点，我们即不能分辨是顺时针还是逆时针在旋转，同时也不能分辨出是向左还是向右的直线运动，因为各种运动方向，在阿基米德螺旋中形成的螺旋结构是相同的。从这个意义上来说，螺旋是一种运动所产生的轨迹，不能用来直接区分运动的方向。因为，可以看到，顺时针旋转 加 从左向右运动，轨迹 等于 逆时针旋转 加 从右向左运动。

【软件下载】

等距螺旋实验演示软件：

https://pan.baidu.com/s/1d7KeVKclptXuvuGI5XMFBA

 

​