Lyk Love painting

Lyk Love painting

一道超出常规的动态规划

题干

【题目描述】

lyk有一块神奇的画布，呈2*n的格子状。lyk现在想在画布上画m幅画，每幅画必须是矩形。为了充分利用画布，画布上的每一个格子都必须属于某一幅画。

每一个格子都有一个魅力值，一幅画的魅力值为其所包含的格子的魅力值的总和。为了不过于展现自己的才华lyk希望这m幅画魅力值的最大值最小。然而他并不知道如何作画才能达到要求，请你帮帮他吧。

【输入】

第一行两个数n，m

第2、第3行每行n个数，表示每个格子的魅力值

【输出】

仅包含一个整数，为最优方案中最大的魅力值最小可能为多少。

【输入样例】

3 3
1 3 2
1 3 2

【输出样例】

4

【提示】

【数据范围】

对于30%的数据,n ≤ 150, m ≤ 30

对于60%的数据,n ≤ 500, m ≤ 50

对于80%的数据,n ≤ 2000, m ≤ 100

对于100%的数据,n ≤ 100000, m ≤ 100

做法：

首先，看到希望使得最大魅力值最小，非常显然的二分答案。
于是难点来到如何去\(check\)答案。

题意实际要求我们做的是将一个\(2*n\)的矩形分割成若干个小矩形，因为二分答案，所以我们要在限定的取值下分割成限定的块，
又由于，当较优的划分成立时，较差的一定可以成立。因此我们只要在分割时保证最优策略，检查最优策略是否能在不超过\(mid\)的前提下，划分成小于等于\(m\)个块，就可以判定答案的可行性了。
这似乎很麻烦，但幸运的是，由于画布是2*n的大矩形，所有的矩形实际上只有以下3种情况

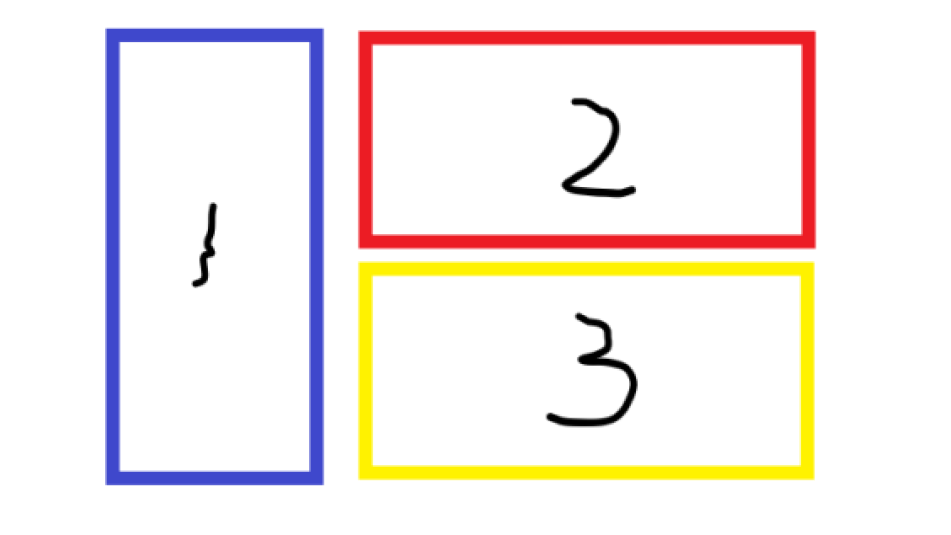
如果假设我们已经铺好了所有的矩形，最后的划分状态一定是一整块竖向的矩形，或者两块由一定数量的小矩形组成的横向的矩形两种情况组成的，也就是

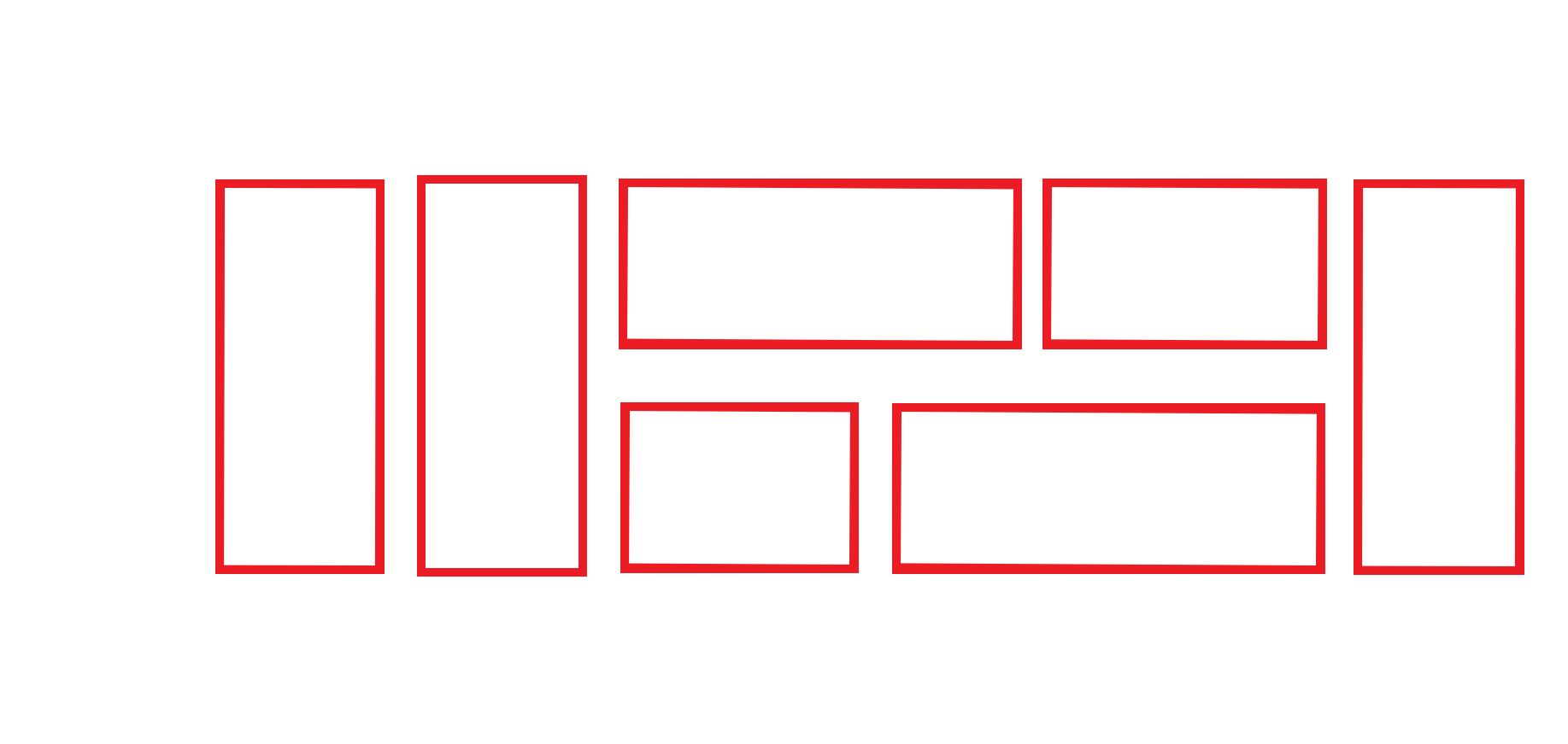
可以想到，对于最终得到的矩形一定是一段一段的（也有可能只有一段），
这样的话，我们可以将每一个完整的一段作为一个状态，进行转移，也就是，动态规划。

于是，我们考虑使用动态规划。
设\(dp[i]\)表示，前\(i\)都已划分好，且最后一块右端为第\(i\)列时，已划分的块数。考虑转移的两张情况，一种为前面提到的"1"矩形，另一种就是由多个"2","3"矩形进行填充。根据最优策略，很容易能想到，这一块中的矩形在总魅力值小于等于限制的前提下，越长越好。
先看朴素方法，对第一种情况，我们直接从左往右找到第一个符合条件的位置j，直接转移即可。对情况二，我们采取同样的方法，但对上下两部分分别进行，各自多次向前找到最长的块，直到无法继续向前为止，这时我们将转移位置定为两者间较短的那一块。
于是得到转移方程

\[dp[i]=min(dp[j_1]+cost(i,j_1),dp[j_2]+\sum_{k=1}^{k<=j_2}) \]

但是，这种方式下的复杂度为\(O(n^2mlogn)\),很显然无法通过此题。
考虑对转移的优化。
二分答案时，对于不同的限制值，分别预处理出每一个第\(i\)列的三种情况（就是前面的那三个矩形）下向前跳的最远位置,\(pre1[i]\),\(pre2[i]\),\(pre3[i]\)。

这样，我们用\(O(n)\)的时间预处理后,就可以在转移时\(O(1)\)地得到每一个最佳决策。
最终复杂度为\(O(nmlgn)\)。

coding:

#include<bits/stdc++.h>
#define N 1000005
#define max(a,b) a>b?a:b
#define f1(i,n,m) for(int i=n;i<=m;++i)
#define f2(i,n,m) for(int i=n;i>=m;--i)
#define ll long long 
#define reset(a,b) memset(a,b,sizeof(a))
#define INF 0x3f3f3f
using namespace std;
template <typename T>
void read(T &x){
    int w=1;x=0;
    char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    x*=w;
}
int n,m;
ll l,r,mid;
ll v[5][N],pre1[N],pre2[N],pre3[N];
ll s1[N],s2[N],s3[N];
int dp[N];
inline bool check(ll lim){	
	pre1[0]=pre2[0]=pre3[0]=0;
	f1(i,1,n){
		pre1[i]=pre1[i-1],pre2[i]=pre2[i-1],pre3[i]=pre3[i-1];
		while(s1[i]-s1[pre1[i]]>lim)pre1[i]++;
		while(s2[i]-s2[pre2[i]]>lim)pre2[i]++;
		while(s3[i]-s3[pre3[i]]>lim)pre3[i]++;
	}//预处理出较每一列在限制条件下能向前跳的最远位置
	reset(dp,INF);
	dp[0]=0;
	int step,p1,p2;
	f1(i,1,n){
		dp[i]=min(dp[i],dp[pre3[i]]+1);//以第一种情况更新状态
		p1=p2=i,step=0;
		while(step<=m&&(p1||p2)){//
			if(p1>p2)p1=pre1[p1];
			else p2=pre2[p2];
			step++;
			dp[i]=min(dp[i],dp[max(p1,p2)]+step);//横向块向前跳
		}
		if(dp[i]>m)return false;	
	}
	return true;
}
signed main(){
	read(n),read(m);
	f1(i,1,2)f1(j,1,n)read(v[i][j]),l=max(v[i][j],l);
	f1(i,1,n){		
		s1[i]=s1[i-1]+v[1][i];
		s2[i]=s2[i-1]+v[2][i];
		s3[i]=s1[i]+s2[i];
	}
	r=s3[n];
	while(l<r){
		mid=(l+r)>>1;
		if(check(mid))r=mid;
		else l=mid+1;
	}
	printf("%lld\n",r);
	return 0;
}

圆满结束