图解算法(三)
递归
1.递归
问题描述,假设有一个上锁的神秘手提箱,要是在一个盒子里,这个盒子里有盒子,而盒子里又有盒子。钥匙就在某个盒子中。为找到钥匙,使用什么算法?
第一种方法:
(1)创建一个要查找的盒子dui
(2)从盒子堆取出一个盒子,在里面找。
(3)如果找到的是盒子,就将其加入盒子堆,以便以后再查找
(4)如果找到钥匙,则成功
(5)回到第二步
第二种方法:
(1)检查盒子中的每样东西
(2)如果是盒子,就回到第一步
(3)如果是钥匙,就成功
第一种方法使用的是while循环:只要盒子堆不为空,就从中取一个盒子,并在其中仔细查找。
伪代码如下
def look_for_key(main_box): pile = main_box.make_a_pile_to_look_through() while pile is not empty: box = pile.grab_a_box(): for item in box: if item.is_a_box(): pile.append(item) elif item.is_a_key(): print "found the key!"
第二种方法使用递归——函数调用自己,
伪代码如下
def look_for_key(box): for item in box: if item.is_a_box(): look_for_key(item) elif item.is_a_key(): print "found the key"
这两种方法的作用相同,但是第二方法更清晰。递归只是让解决方案更加清晰,并没有性能上的优势。实际上在有些情况下,使用循环的性能更好。
2.基线条件和递归条件
由于递归函数调用自己,因此编写这样的函数很容易出错,进而导致无限循环。
例如,假设你要编写一个像下面一样的倒计时函数

可以使用递归的方式来写
def countdown(i): print i countdown(i-1)
如果运行上述代码,将无限运行,编写递归函数时,必须告诉他何时停止递归。正因为如此,每个递归函数都有两部分:基线条件和递归条件。递归条件指的是函数调用自己,而基线条件则指的是函数不再调用自己,从而避免无限循环。
def countdown(i): print i if i<= 1: return else: countdown(i-1)
3.栈
本节将介绍一个重要的编程概念——调用栈(call stack)。调用栈不仅对编程来说很重要,使用递归时也必须理解这个概念。
假设你去野外烧烤,并为此创建了一个待办事项清单——一叠便条。
使用一叠便条:插入的待办事项放在清单的最前面;读取待办事项时,只读取最上面的那个,并将其删除。只有两个操作:压入和弹出。

这种数据结构成为栈。
3.1 调用栈
计算机在内部使用被称为调用栈的栈。
def greet(name): print "hello," + name + "!" greet2(name) print "getting ready to say bye..." bye()
这个函数问候用户,再调用另外两个函数。这两个函数的代码如下。
def greet2(name): print "How are you," + name + "?" def bye(): print "ok bye!"
下面详细介绍调用函数时发生的情况
假设你调用greet("maggie"),计算机首先为该函数调用分配一块内存
我们来使用这些内存。变量name被设置为maggie,这需要存储到内存中。

每当调用函数时,计算机都像这样将函数调用涉及的所有变量的值存储到内存中。接下来,打印hello,maggie!,再调用greet2("maggie")。同样,计算机也为这个函数调用分配一块内存。

计算机使用一个栈来表示这些内存块,其中第二个内存块位于第一个内存块上面。你打印how are you,maggie?,然后从函数调用返回。此时,栈顶的内存块被弹出。

现在,栈顶的内存块是函数greet的,这意味着你返回到了函数greet。当你调用函数greet2时,函数greet只执行了一部分。这是一个很重要的概念:调用另一个函数时,当前函数暂停并处于未完成状态。该函数的所有变量的值都还在内存中。执行完函数greet2后,你回到函数greet,并从离开的地方开始接着往下执行:首先打印gettng ready to say bye,再调用函数bye。

在栈顶添加了函数bye的内存块。然后,你打印ok bye!,并从这个函数返回。

现在你又回到了函数greet。由于没有别的事情要做,你就从函数greet返回。这个栈用于存储多个函数的变量,被称为调用栈。
3.2 递归调用栈
递归函数也使用调用栈。来看看递归函数factorial的调用栈。factorial(5)写作5!其定义如下:5!=5*4*3*2*1。下面是计算阶乘的递归函数。
def fact(x): if x == 1: return 1 else: return x * fact(x-1)
下面来详细分析调用fact(3)时调用栈时如何变化的。注意,栈顶的方框指出了当前执行到了什么地方。
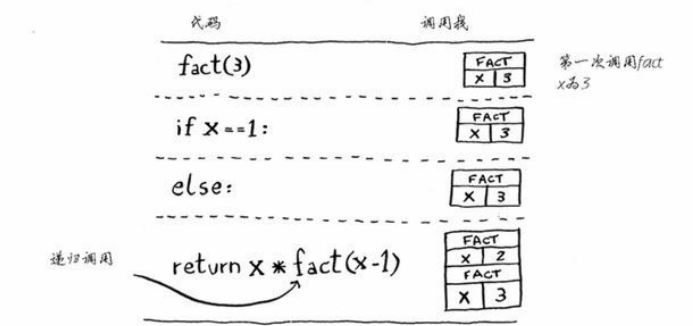

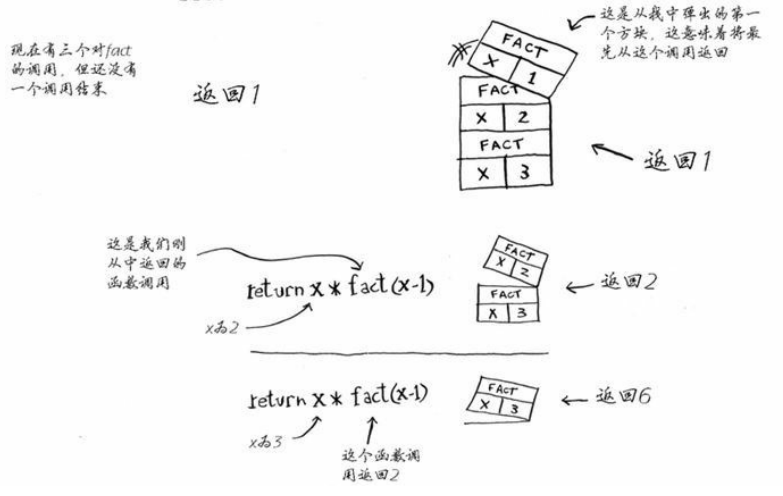
注意,每个fact调用都有自己的x变量。在一个函数调用中不能访问另一个的x变量。
栈在递归中扮演着重要的角色。回到寻找钥匙的方法。第一种方法,创建了一个待查找的盒子堆,因此你始终都知道还有哪些盒子需要查找。但是使用递归方法时,并没有盒子堆。既然没有盒子堆,那算法怎么知道还有哪些盒子需要查找呢?

此时,调用栈类似于下面这样。

原来“盒子堆”存储在了栈中。这个栈包含未完成的函数调用,每个函数调用都包含还未检查完的盒子。使用栈很方便,因为你无须跟踪盒子堆——栈替你做了。
使用栈很方便,但也有代价:存储详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存,如果栈很高,就意味着计算机存储了大量函数调用的信息。在这种情况下,有两种选择:
- 重新编写代码,转而使用循环
- 使用尾递归。这是一个高级递归主题,在此不做介绍。。。。
4.小结
- 递归指的是调用自己的函数
- 每个递归函数都有两个条件:基线条件和递归条件
- 栈有两种操作:压入和弹出
- 所有函数调用都进入调用栈
- 调用栈可能很长,占用大量内存


 浙公网安备 33010602011771号
浙公网安备 33010602011771号