图解算法(二)
选择排序
1.内存的工作原理

fe0ffeeb是一个内存单元的地址。
需要将数据存储到内存时,你请求计算机提供存储空间,计算机给你一个存储地址。需要存储多项数据时,有两种基本方式——数组和链表。
2.数组和链表
有时候,需要在内存中存储一系列元素。加入你要编写一个管理待办事项的应用程序,需要将这些待办事项存储在内存中。
鉴于数组更容易掌握,我们先将待办事项存储在数组中。使用数组意味着所有待办事项在内存中都是相连的(紧靠在一起的)。

现在假设你要添加第四个待办事项,但后面的那个抽屉放着别人的东西。在这种情况下,你需要请求计算机重新分配一块可容纳四个待办事项的内存,再将所有待办事项都移到那里。同样,在数组中添加新元素也可能很麻烦。如果没有了空间,就得移到内存的其他地方,因此添加新元素的速度也会很慢。一种解决之道是“预留座位”:即便当前只有3个待办事项,也请计算机提供10个位置,以防需要添加待办事项。但是存在两个缺点:
- 你额外请求的位置可能根本用不上,这将浪费内存。
- 待办事项超过10个后,还得转移
对于这种问题,可使用链表来解决。
2.1链表
链表中的元素可存储在内存的任何地方。
链表的每个元素都存储了下一个元素的地址,从而使一系列随机的内存地址串在一起。

在链表中添加数据很容易:只需要将其放入内存,并将其地址存储到前一个元素中。
使用链表时,根本不需要移动元素。链表的优势在插入元素方面,那数组的优势又是什么?
2.2 数组
在需要读取链表的最后一个元素时,你不能直接读取,一位你不知道它所处的地址,必须先访问元素#1,从中获取元素#2的地址,再访问元素#2并从中获取元素#3的地址,一次类推,直到访问最后一个元素。需要同时读取所有的元素时,链表的效率很高:你读取第一个元素,根据其中的地址再读取第二个元素,以此类推。
数组与此不同:你知道其中每个元素的地址。例如,假设有一个数组,它包含五个元素,起始地址为00,那么元素#5的地址是多少呢?04!。需要随机读取元素时,数组的效率很高,因为可迅速找到数组的任何元素。
2.3 术语
数组的元素带编号,编号从0开始。元素的位置成为索引。
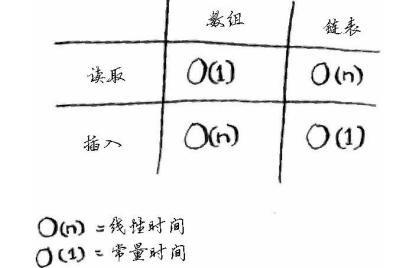
下面列出了常见的数组和链表操作的运行时间。
2.4 在中间插入
需要在中间插入元素时,使用链表时,插入元素很简单,只需要修改它前面的那个元素指向的地址。而使用数组时,则必须将后面的元素都向后移。
2.5 删除
如果要删除元素呢?链表也是更好的选择,因为只需修改前一个元素指向的地址即可。而使用数组时,删除元素后,必须将后面的元素都向前移。
下面是常见的数组和链表操作的运行时间
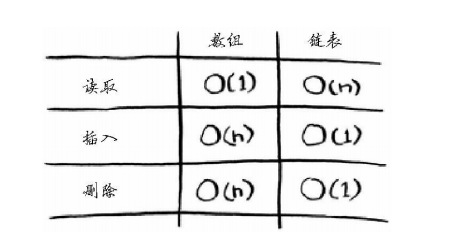
需要指出的是,仅当能够立即访问要删除的元素时,删除操作的运行时间才为O(1)。
数组和链表哪个用的更多呢?显然要看情况。但数组用的很多,因为它支持随机访问。有两种访问方式:随机访问和顺序访问。顺序访问意味着从第一个元素开始逐个读取元素。链表只能顺序访问:要读取链表的第十个元素,得先读取前九个元素,并沿链接找到第十个元素。随机访问意味着可直接跳到第十个元素。
3.选择排序
假设你的计算机存储了很多的乐曲。对于每个乐队,你都记录了其作品被播放的次数。

你要将这个列表按播放次数从多到少的顺序排列,从而将你喜欢的乐队排序。
一种方法是遍历这个列表,找出作品播放次数最多的乐队。并将该乐队添加到一个新列表中。
再次这样做,找出播放第二多的乐队。继续这样做,得到一个列表。要找出播放次数最多的乐队,必须检查列表中的每一个元素。这需要的时间为O(n)。因为需要执行n次,所以需要的总时间为O(n2)。
随着排序的进行,每次需要检查的元素数在逐渐减少,最后一次需要检查的元素都只有一个。既然如此,为什么运行时间还是O(n2),大O表示法省略常数,简单写作O(n2)。
示例代码
将数组元素从小到大的顺序排列。先编写一个用于找出数组中最小元素的函数。
def findSmalleset(arr): smallest = arr[0] <----存储最小的值 smallest_index = 0 <----存储最小元素的索引 for i in rang(1,len(arr)): if arr[i] < smallest: smallest = arr[i] smallest_index = i return smallest_index
现在可以使用这个函数来编写选择排序算法了。
def selectionSort(arr): newArr = [] for i in range(len(arr)): smallest =findSmallest(arr) newArr.append(arr.pop(smallest)) return newArr print selectionSort([5,3,6,2,10])


