图解算法（一）

1.二分查找

python2.7 实现代码

 1 #!/usr/bin/python
 2 def binary_search(list,item):
 3    low=0
 4    high= len(list)-1
 5 
 6    while low<=high:
 7      mid = (low+high) / 2
 8      guess = list[mid]
 9      if guess == item:
10         return mid
11      if guess > item:
12         high = mid -1
13      else:
14         low = mid+1
15    return None
16 my_list = [1,3,5,7,9]
17 
18 print binary_search(my_list, 3)
19 print binary_search(my_list ,-1)

函数binary_search接收一个有序数组和一个元素。如果指定元素包含在数组中，这个函数将返回其位置。你将跟踪要在你其中查找的数组部分——开始时为整个数组。

low = 0

high = len(list)-1

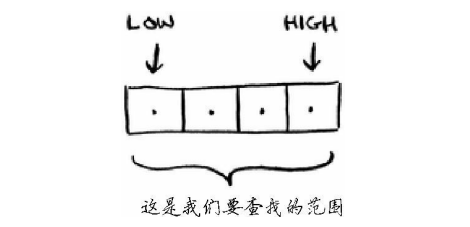
你每次都检查中间的元素。

mid = (low+high) / 2    <------如果（low+high）不是偶数，Python自动将mid向下取整。

guess = list[mid]

如果猜的数字小了，就相应地修改low。

if guess < item:

  low= mid +1

如果猜测的数字大了，就修改high的值

2.大O表示法

大O表示法是一种特殊的表示法，支出了算法的速度有多快。

2.1 算法的运行时间以不同的速度增加

   大O表示法指出了算法有多快。例如，假如列表包含n个元素。简单查找需要检查每个元素，因此需要执行n次操作使用大O表示法，这个运行时间为O(n)。大O表示法指的并非是以秒为单位的速度。大O表示法让你能够比较操作数，它指出了算法运行时间的增速。

  再比如，为检查长度为n的列表，二分查找需要执行log n次操作。使用大O表示法表示O(log n)。

2.2 理解不同的大O运行时间

一种方法是以每次画一个的方式画16个格子，需要画16个格子。运行时间为O(n)

另一种方法是将纸张对折四次。运行时间为O(log n)

2.3 大O表示法指出了最糟情况下的运行时间

简单查找的运行时间总是为O(n)。查找A时，一次就找到了，这是最佳的情况，但是大O表示法说的是最糟的情形。

2.4 常见的大O运行时间

下面按从快到慢的顺序列出

• O(log n)，也叫对数时间，这样的算法包括二分查找
• O(n)，也叫线性时间，包括简单查找
• O(n*log n)，包括快速排序——一种速度较快的排序算法
• O(n²)，包括选择排序——一种速度较慢的排序算法
• O(n!)，包括接下来介绍的旅行商问题的解决方案

2.5 旅行商

一位旅行商，他需要前往5个城市，同时要确保旅程最短,可考虑前往这些城市的各种可能顺序。涉及n个城市时，需要执行时间为O(n!)，即阶乘时间。