3.6 Left and Right Inverses; Pseudoinverse 阅读笔记

左逆, 右逆, 伪逆

reference的内容为唯一教程, 接下来的内容仅为本人的课后感悟, 对他人或无法起到任何指导作用.

Reference

1. Course website: Left and Right Inverses; Pseudoinverse | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 33: Left and right inverses; pseudoinverse (mit.edu)
4. Extra reading: MIT—线性代数笔记 33 左右逆和伪逆 - 知乎 (zhihu.com)

---

最后一部分是左逆, 右逆, 和伪逆. 书上没找到, Lecture 讲的也很快, 很粗糙. 到最后沦为掉包.

2-Sided Inverse

对 \(r = m = n\) 的矩阵 \(A\), 有:

\[A A^{-1} = I = A^{-1} A \]

Left Inverse

对 \(r = n\) 的矩阵 \(A\), 有 \(\text{rank}(A^{\mathrm{T}}A)=n\), 为 n 阶可逆方阵. 于是有 $(A^{{\mathrm{T}}A)}(A^{\mathrm{T}}A) = I \Rightarrow A_{\text{left}}^{-1}A=I $. 于是定义左逆:

\[A_{\text{left}}^{-1} = (A^{\mathrm{T}}A)^{-1}A^{\mathrm{T}} \]

此时还有:

\[A A_{\text{left}}^{-1} = A (A^{\mathrm{T}}A)^{-1}A^{\mathrm{T}} = P_{m \times m} \]

将 \(\mathbb{R}^{m}\) 投影到 \(C(A)\). 而且 \(A_{\text{left}}^{-1}\) 是距离 \(AM=I\) 最近的解.

Right Inverse

对 \(r = m\) 的矩阵 \(A\), 有 \(\text{rank}(AA^{\mathrm{T}})=m\), 为 m 阶可逆方阵. 于是有 $(AA^{{\mathrm{T}})(AA}{\mathrm{T}})^{-1} = I \Rightarrow A A_{\text{right}}^{-1}=I $. 于是定义右逆:

\[A_{\text{right}}^{-1} = A^{\mathrm{T}}(AA^{\mathrm{T}})^{-1} \]

此时还有:

\[A_{\text{right}}^{-1}A = A^{\mathrm{T}}(AA^{\mathrm{T}})^{-1}A = P_{n \times n} \]

将 \(\mathbb{R}^{n}\) 投影到 \(C(A)\). 而且 \(A_{\text{right}}^{-1}\) 是距离 \(MA=I\) 最近的解.

Pseudoinverse

How It Works?

再次扒下来别人画的一个图:

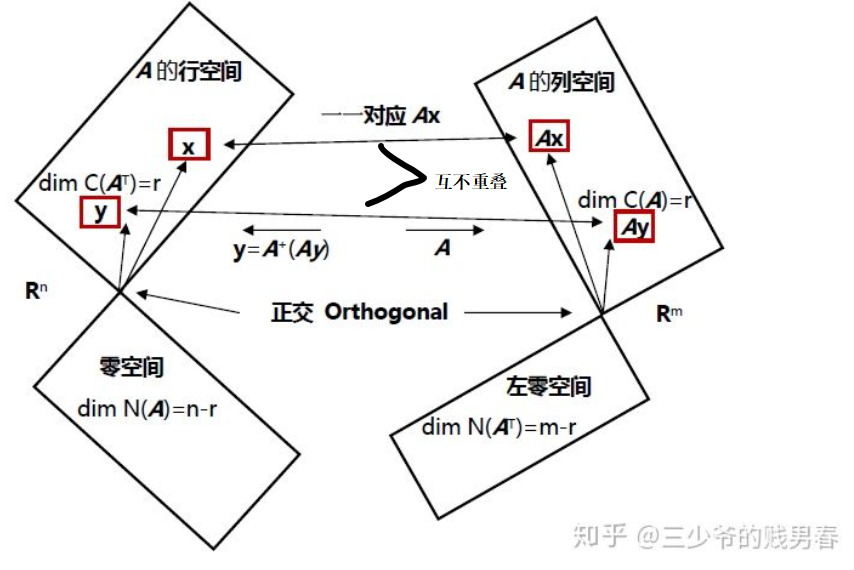
观察此图, 行空间的向量经过 \(A \bm{x}\) 来到列空间, 而列空间的向量经过 \(A^{-1}\bm{y}\) 回到行空间. 行空间和列空间的秩都为 \(r\), 满足一一映射, 互不重叠. 如果线性变换限制在行空间和列空间之间, \(A\) 一定是可逆的, 把"逆"矩阵记作 \(A^+\).

但是很不幸, 有零空间的存在, 从零空间一个映射 \(A \bm{x} = 0\), 再返回去, 难道有向量左乘零向量能回到 \(\bm{x}\) 吗? 不能, 因此不可逆. 反方向也一样. 正因为零空间的存在, 导致不可逆.

因此伪逆就是找行空间与列空间之间的一一映射, 至于零空间就不管了, 爱咋咋地. 不过现在有个问题需要证明, 为啥行空间与列空间一一映射呢?

Bijection Proof

复习一下离散的知识. 设函数 \(f:A->B\)

• 证明单射：证明当 \(x≠y\) 时，\(f(x)≠f(y)\)
• 证明满射：证明对于所有的 \(b∈B\)，存在 \(a∈A\)，使得 \(f(a)=b\)
• 证明双射：证明单射和满射

1. 先证明满射:

任意一个列空间的向量 \(\bm{b}\), 都是列向量的线性组合, 线性组合等价于矩阵乘法, 也就是说任何一个列空间的向量都在 \(A \bm{x}\) 张成的空间内, 因此 \(A \bm{x} = \bm{b}\) 必有解.

2. 再证明双射:

即如果 \(\bm{x}, \bm{y} \in C(A^{\mathrm{T}})\), \(x \neq y\). 则 \(A \bm{x} \neq A \bm{y}\).

反证法, 假设有 \(A \bm{x} = A \bm{y}\), 则 \(A (\bm{x}-\bm{y}) = \boldsymbol{0}\). 而 \(\bm{x}-\bm{y} \in C(A^{\mathrm{T}})\) (运算封闭性), \(\bm{x}-\bm{y}\) 还是一个零解所以在 \(N(A)\) 内. 零空间和行空间的交集只有零向量, 于是 \(\bm{x}-\bm{y}=\boldsymbol{0}\), 即 \(\bm{x}=\bm{y}\), 矛盾. 因此原假设成立, 双射成立.

于是一一映射的证明完成!

Calculation

求伪逆矩阵 \(A^+\) 的一个方法是利用奇异值分解 \(A=U\Sigma V^{\mathrm{T}}\), 其中对角阵 \(\Sigma\) 是由矩阵奇异值排列在对角线上构成的 \(m \times n\) 矩阵, 其秩为 \(r\). 则伪逆矩阵 \(A^+\) 为 \(n \times m\) 矩阵, 矩阵的秩也为 \(r\).

\(U\) 和 \(V\) 都是可逆的, 而 \(\Sigma\) 不可逆, 问题转变为求 \(\Sigma\) 的伪逆.

这里面 \(\Sigma=\left[\begin{array}{c c c|c}\sigma_1&&&\\&\ddots&&\\&&\sigma_r&\\\hline&&&\begin{bmatrix}0\end{bmatrix}\end{array}\right]\), 对角线非零的部分来自\(A^{\mathrm{T}}A,\ AA^{\mathrm{T}}\)比较好的部分, 剩下的来自(左)零空间.

而 \(\Sigma\) 矩阵的伪逆 \(\Sigma^+=\left[\begin{array}{c c c|c}\frac{1}{\sigma_1}&&&\\&\ddots&&\\&&\frac{1}{\sigma_r}&\\\hline&&&\begin{bmatrix}0\end{bmatrix}\end{array}\right]\). 这里的逆和伪逆 左上角. 右上角, 左下角 三个部分必须是对角阵和两个零阵, 这样方可保证行空间与列空间之间一一映射. 右下角 代表零空间们, 可以任取, 但是通常也是零阵. 伪逆矩阵和 \(A^+\) 维度一样, 是一个 \(n\times m\) 矩阵.

\[\Sigma\Sigma^+=\left[\begin{array}{c c c|c}1&&&\\&\ddots&&\\&&1&\\\hline&&&\begin{bmatrix}0\end{bmatrix}\end{array}\right]_{m\times m}, \Sigma^+\Sigma=\left[\begin{array}{c c c|c}1&&&\\&\ddots&&\\&&1&\\\hline&&&\begin{bmatrix}0\end{bmatrix}\end{array}\right]_{n\times n} \]

观察 \(\Sigma\Sigma^+\) 和 \(\Sigma^+\Sigma\) 不难发现, \(\Sigma\Sigma^+\) 是将向量投影到列空间上的投影矩阵, 而 \(\Sigma^+\Sigma\) 是将向量投影到行空间上的投影矩阵. 我们不论是左乘还是右乘伪逆, 得到的不是单位矩阵, 而是投影矩阵, 该投影将向量带入比较好的空间 (行空间和列空间, 而不是(左)零空间).

\(A\) 的伪逆则为:

\[A^+=V\Sigma^+U^{\mathrm{T}} \]