3.5 Linear Transformations and Change of Basis 阅读笔记

线性变换与基变换

reference的内容为唯一教程, 接下来的内容仅为本人的课后感悟, 对他人或无法起到任何指导作用.

Reference

1. Course website: Linear Transformations and their Matrices | Linear Algebra | Mathematics | MIT OpenCourseWare and Change of Basis; Image Compression | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili and 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 30: Linear transformations and their matrices (mit.edu) and Lecture 31: Change of basis; image compression (mit.edu)
4. Extra Video: Abstract vector spaces | Chapter 16, Essence of linear algebra - YouTube

---

线性变换贯穿了整个笔记的始终. 矩阵乘法代表了一个线性变换. 从始至终, 我一直站在几何的角度理解向量, 把向量当作一个箭头. 哪怕是有坐标的向量, 我也会默认画一组单位正交向量作为基, 如平面直角坐标系.

但事实上, 向量是抽象的, 它可以是任何对象, 比如函数, 只要满足一些公理 (Axiom) 即可.

Abstract Vectors

向量需要满足加法和数乘运算的封闭性, 为了满足这两个性质, 人们找出了 8 条公理, 如果任何一个对象, 定义了加法和数乘两种运算, 如果满足这 8 条公理, 那么它就可以视作向量.

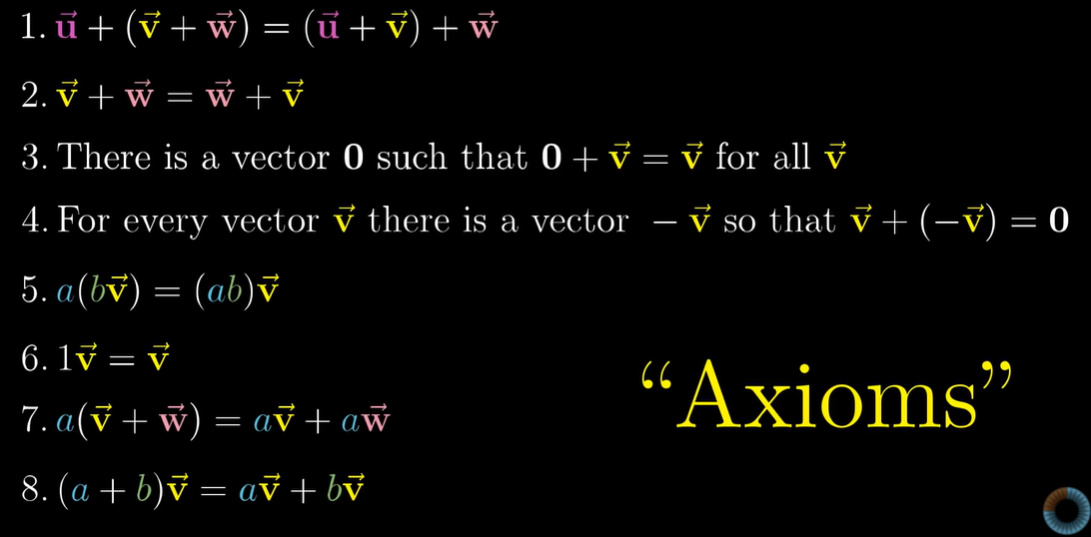
Linear Transformation

线性变换最初也是用抽象的 vectors, 再用抽象的方法定义的. 线性变换是从一个向量空间到另一个向量空间的映射, 满足:

\[\begin{aligned} T(\bm{v}+\bm{w}) &=T(\bm{v})+T(\bm{w})\\ T(c \bm{v}) &=cT(\bm{v})\\ \end{aligned} \]

有一个有趣的性质是: \(T(c \boldsymbol{0}) = cT(\boldsymbol{0}) = T(\boldsymbol{0})\), 于是 \(T(\boldsymbol{0}) = 0\).

这种定义虽然可以囊括一切, 十分严谨, 但是从中什么也看不出来. 而如果按照之前 "Grid lines paralleled and evenly spaced" 的话, 就十分直观. 因此, 只有从几何上理解, 才能更给我们一个 Big Picture 让我们知道在做什么, 而不是盯着符号, 变量在那里推着公式, 却不知道有什么用. 因此, 是很有必要让抽象的向量和抽象的线性变换获得一个几何表示的.

我们要给一个向量坐标 (Coordinates) 的概念, 在此之后便可以将抽象的线性变换 \(T(\bm{x})\) 用矩阵表示 \(A \bm{x}\).

Coordinates

任何一个向量 \(\bm{v}\), 都可以找到一组基 \(\bm{v}_1, \bm{v}_2, \cdots , \bm{v}_n\). 向量可以由这组基唯一进行表示:

\[\begin{aligned} \bm{v} &= c_1 \bm{v}_1 + \cdots + c_n \bm{v}_n\\ T(\bm{v}) &= c_1 T(\bm{v}_1) + \cdots + c_n T(\bm{v}_n) \end{aligned} \]

则向量 \(\bm{v}\) 在基 \(\bm{v}_1, \bm{v}_2, \cdots , \bm{v}_n\) 下的坐标表示为 \(\begin{bmatrix} c_1 & \cdots & c_n \\\end{bmatrix}^{\mathrm{T}}\), 每一个基向量 \(\bm{v}_i\) 的坐标表示为 \(\begin{bmatrix} v_1=0 & \cdots & v_{i-1} = 0 & v_i=1 & v_{i+1} = 0 & \cdots & v_n = 0 \\\end{bmatrix}\). 于是这个向量和这组基全都变成了坐标, 再按照我们的平面直角坐标系/空间直角坐标系的方式实现可视化.

Describing \(T(\bm{x})\) with Matrix

• 对输入向量 \(\bm{v}\), 由 \(\bm{v}_1, \cdots , \bm{v}_n\) 表示, 因此可以获得 \(\mathbb{R}^{n}\) 的坐标.
• 对输出向量 \(\bm{w}\), 由 \(\bm{w}_1, \cdots , \bm{w}_m\) 表示, 因此可以获得 \(\mathbb{R}^{m}\) 的坐标.

然后求出从输入坐标到输出坐标的矩阵映射, 即可求出线性变换的矩阵表示.

比如: \(T(c_1+c_2x+c_3x^{2})=\displaystyle\frac{d}{dx}(c_1+c_2x+c_3x^{2})=c_2+2c_3x\).

此时 \(\bm{v}_1 = 1, \bm{v}_2 = x, \bm{v}_3 = x^{2}\), \(\bm{w}_1 = 1, \bm{w}_2 = x\).

于是输入坐标为 \((c_1, c_2, c_3)\), 输出坐标为 \((c_2, 2c_3)\). 需要一个 \(2 \times 3\) 的矩阵 \(A\) 进行转换.

求得 \(\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 2 \\\end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\\end{bmatrix} = \begin{bmatrix} c_2 \\ 2c_3 \\\end{bmatrix}\), 于是 \(A = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 2 \\\end{bmatrix}\).

但是我有一点困惑: 为什么输出的向量用的基和输入不一样呢? 因为前面 3Blue1Brown 那里说, \(\bm{y} = A \bm{x}\) 是将变换前的基下原向量的坐标, 变换到同样的基下新的向量的坐标; 或者是将变换后的基下向量的坐标, 变换到变换前的基下同一向量的坐标. 但是这里用的是一个和变换不一样的基向量下新的坐标, 而没有和变换前的基保持不变.

Lecture 举的第一个例子, 投影矩阵, 投影前后用的都是一样的基. 第二个例子也就是这个, 我觉得是因为维度变换, 削掉了一维, 本来输出坐标应该是 \((0, c_2, 2c_3)\) 的. 但是我想, 如果设恒等变换如 \(T(c_1+c_2x+c_3x^{2})=c_1+c_2x+c_3x^{2}\), 但是我对输出向量换成 \(\bm{w}_1 = x ^{2}, \bm{w}_2 = x\), \(w_3 = 1\), 求得的 \(A\) 就是 \(\begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\\end{bmatrix}\), 并不是 \(I\). 那这时 \(A\) 的数值代表了什么? 线性变换的基向量在新的基下的坐标? 我有点糊涂了.

Change of Basis

这一部分没什么区别.

对于同一向量:

• 变换后基坐标->变换前基坐标: \(\bm{y} = A \bm{x}\)
• 变换前基坐标->变换后基坐标: \(\bm{x} = A^{-1} \bm{y}\)

变基公式, 在 \(S\) 基下变换 \(A\) 写作:

\[A \rightarrow S^{-1}AS \]