3.2 Complex Matrices and Fast Fourier Transform 阅读笔记

复矩阵与快速傅里叶变换

reference的内容为唯一教程, 接下来的内容仅为本人的课后感悟, 对他人或无法起到任何指导作用.

Reference

1. Course website: Complex Matrices; Fast Fourier Transform (FFT) | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 26: Complex matrices; fast Fourier transform (mit.edu)
4. Extra reading: 数字信号处理教程 第三版 程佩青 编

---

本讲主要介绍复矩阵有没有类似实对称矩阵特征值特征向量这种性质, 发现还真有, 但是需要满足共轭对称. 在此之前需要介绍复数向量, 定义复数向量的点积运算, 之后会提到一个应用: 傅里叶矩阵和快速傅里叶变换, 用于离散傅里叶变换 (DFT).

本文假设已对信号与系统, 数字信号处理有基本认识.

本文粗略带过 FFT, 因为感觉用不上了.

Complex Vectors

先介绍复数向量, 我们不妨换一个字母符号来表示: \(\bm{z}=\begin{bmatrix}z_1 & z_2 & \cdots & z_n\end{bmatrix}^{\mathrm{T}}\), 向量的每一个分量都是复数. 此时 \(\bm{z}\) 不再属于 \(\mathbb{R}^n\) 实向量空间, 它现在处于 \(\mathbb{C}^n\) 复向量空间.

• Length: \(\left\vert \bm{z} \right\vert ^{2} = \displaystyle\sum_{i=1}^{n} \left\vert \bm{z}_i \right\vert ^{2} = \bar{\bm{z}}^{\mathrm{T}}\bm{z}\)
• Inner Product: \(\bm{z}_1 \cdot \bm{z}_2 = \bar{\bm{z}}_1^{\mathrm{T}}\bm{z}_2\)

对比实向量, 我们计算复向量的模不再是用向量内积自己开根号了, 而是需要用共轭向量内积自己开根号, 这是高中知识, 不再赘述.

我们把共轭转置乘以原向量记为 \(\bm{z}^{\mathrm{H}}\bm{z}\), \(\mathrm{H}\) 作 Hermite. 因此向量的内积 \(\bm{z}_1 \cdot \bm{z}_2\) 可以看作 \(\bm{z}_1^{\mathrm{H}}\bm{z}_2\). Hermite 是复向量中的"转置".

Complex Matrices

复矩阵满足"共轭对称"的话则也会有和实对称矩阵一样的性质:

• 实特征值
• "标准正交"/"orthonormal" 的特征向量

那么什么是"共轭对称呢", 大概猜到了, 就是 \(A^{\mathrm{H}} = A = \bar{A}^{\mathrm{T}}\).

Unitary Matrices

标准正交涉及到了内积, 所以显然在这里也得按照复数的规则内积, 于是起了个新名字酉矩阵 (Unitary Matrices) \(Q=\begin{bmatrix} \bm{q}_1 & \bm{q}_2 & \cdots & \bm{q}_n \\\end{bmatrix}\), 满足:

\[\bar{\bm{q}}_i^{\mathrm{T}}\bm{q}_j=\bm{q}_i^{\mathrm{H}}\bm{q}_j=\begin{cases}0\quad i\neq j\\1\quad i=j\end{cases} \]

对于复矩阵, 有 \(Q^{\mathrm{H}}Q=I\).

Discrete Fourier Transform (DFT)

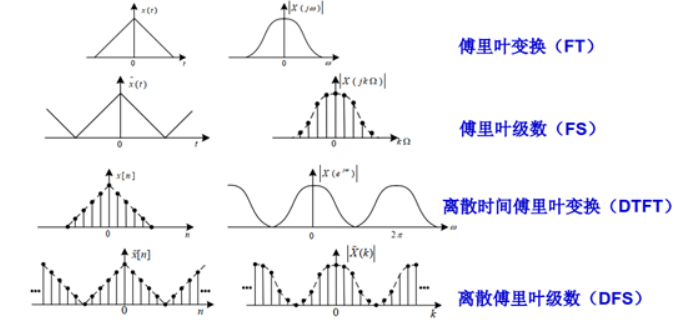
傅里叶变换用来将时域的信号转化为频域的信号. 时域和频域可能会离散/连续, 可能会周期/非周期. 它们之间满足以下关系:

\[\begin{cases} \text{连续} \Leftrightarrow \text{非周期} \\ \text{离散} \Leftrightarrow \text{周期} \end{cases} \]

比如时域离散周期, 则频域周期离散. 时域连续周期, 频域非周期离散...

Continuous Time Fourier Transform (CTFT/FT)

自然界的信号一般是连续非周期的信号, 连续傅里叶变换后也是连续非周期. 有公式:

\[\begin{cases} X(j\Omega) &= \displaystyle \int_{-\infty}^{\infty} x(t)e^{-j\Omega t} \mathrm{d}t \\ x(t) &= \displaystyle\frac{1}{2\pi}\int_{-\infty}^{\infty} X(j\Omega)e^{j\Omega t} \mathrm{d}\Omega \end{cases} \]

Discrete Time Fourier Transform (DTFT)

然而计算机接收信号的时候, 时域要采样, 变成离散非周期, 则离散傅里叶变换后频域是连续周期的. 这时有:

\[\begin{cases} X(e^{j\Omega}) &= \displaystyle \sum_{n=-\infty}^{\infty} x[n]e^{-j\Omega n}\\ x[n] &= \displaystyle\frac{1}{2\pi}\int_{-\pi}^{\pi} X(e^{j\Omega})e^{j\Omega n} \mathrm{d}\Omega \end{cases} \]

Discrete Fourier Series (DFS)

然而计算机也要处理和储存频域的信号, 也需要采样, 这时时域仍然离散, 频域周期. 频域也要离散, 时域也需要周期化. 对于时域离散周期化的信号, 可以用离散傅里叶级数表示 (假设周期为 \(N\)):

\[\begin{cases} \tilde{X}[k] &= \displaystyle \sum_{n=0}^{N-1} \tilde{x}[n]e^{-j\frac{2\pi}{N}nk}\\ \tilde{x}[n] &= \displaystyle\frac{1}{N}\sum_{k=0}^{N-1} \tilde{X}[k]e^{j\frac{2\pi}{N}nk} \end{cases} \]

用图可以表示如下:

Discrete Fourier Transform (DFT)

但是通常来说时域离散信号并不是周期的, 计算机也只能处理有限长度的时域和频域信号, 怎么办呢? 如果信号有限长度, 我们可以在 0 至 N-1 处取 N 个点, 再以 N 为周期延拓, 这样就可以做 DFS 了, 对于变换后的频域, 我们也从 0 至 N-1 取 N 个点. 反之逆变换是对频域取的 N 个点周期性延拓, 做 DFS 的逆变换回到时域, 再截取一个周期的 N 个点. 这样便得到一个 N 点序列和另一个 N 点序列的映射:

\[\begin{cases} {X}[k] &= \displaystyle \sum_{n=0}^{N-1} x[n]e^{-j\frac{2\pi}{N}nk}\\ {x}[n] &= \displaystyle\frac{1}{N}\sum_{k=0}^{N-1} {X}[k]e^{j\frac{2\pi}{N}nk} \end{cases} \]

其中 \(n, k \in [0, N-1]\) 且 \(n, k \in \mathbb{Z}\). \(X[k]\) 为 \(\tilde{X}[k]\) 的 \(N\) 点截断, \(x[n]\) 同理.

如果时域信号长度大于 \(N\), 但是却 \(N\) 点截断的情况, 在这里不在展开, 详见数字信号处理.

Matrices Representation of DFT

DFT 作为 N 点序列到 N 点序列的一个映射, 是可以用矩阵表示的. 设时域信号 \(\bm{x} = \begin{bmatrix} x[0] & \cdots & x[N-1] \\\end{bmatrix}^{\mathrm{T}}\), 频域信号 \(\bm{X} = \begin{bmatrix} X[0] & \cdots & X[N-1] \\\end{bmatrix}^{\mathrm{T}}\), 则有:

\[\bm{X} = F_N \bm{x} \]

其中设 \(W_N = e^{j\frac{2\pi}{N}}\), 则 \(F_N\) 为:

\[F_N = \begin{bmatrix}1&1&1&\cdots&1\\1&W_N&W_N^2&\cdots&W_N^{N-1}\\1&W_N^2&W_N^4&\cdots&W_N^{2(N-1)}\\\vdots&\vdots&\vdots&\ddots&\vdots\\1&W_N^{N-1}&W_N^{2(N-1)}&\cdots&W_N^{(N-1)^2}\end{bmatrix} \]

相当于对时域信号进行线性变换到了频域.

给出结论, \(F_N\) 的列向量正交. 但是因为长度不为 1, 因此并非 Unitary. 需要除以 \(\sqrt{N}\).

Fast Fourier Transform (FFT)

如果用这种方式求 DFT, 那可太慢了. 对于傅里叶矩阵, \(F_n\) 和 \(F_{2n}\) 之间有着特殊的关系. 经过一系列推导 (早忘了) 可得:

\[F_{2n} = \begin{bmatrix} I & D \\ I & -D \\\end{bmatrix} \begin{bmatrix} F_n & 0 \\ 0 & F_n \\\end{bmatrix} P = \begin{bmatrix} IF_n & DF_n \\ IF_n & -DF_n \\\end{bmatrix} P \]

\(D\) 为对角矩阵, \(P\) 为 \(2n \times 2n\) 的置换矩阵, 按照某种规则直接写出. 只要知道 \(F_n\), 就能直接写出 \(F_{2n}\). 而 \(F_1 = \begin{bmatrix} 1 \\\end{bmatrix}\).

用二分的方式可以大幅加速 DFT 的计算过程. 原来需要 \(n^2\) 的运算现在只需要\(\displaystyle \frac{n}{2}\log_2n\) 就可以实现了.

下一讲将继续介绍特征值, 特征向量及正定矩阵.