2.10 Geometric View of Eigenvalues and Eigenvectors 阅读笔记
特征向量和对角化的几何意义 (涉及基变换)
reference的内容为唯一教程,接下来的内容仅为本人的课后感悟,对他人或无法起到任何指导作用。
Reference
- Extra videos (3Blue1Brown):
特征值和特征向量有什么几何性质呢? 3Blue1Brown 从线性变换的角度进行了补充.
介绍之前, 需要补充一个很重要很难懂的概念: 基变换.
Change of Basis
Same Coordinates, Different Vectors
线性变换 \(\bm{y} = A \bm{x}\) 是什么意思呢? 其实是坐标不变, 但对应的基从原来的变成了新的, 因此向量发生了改变.
比如原来的基为平面直角坐标系, 新的基为逆时针旋转 90° 的 \(\begin{bmatrix} 0 & -1 \\ 1 & 0 \\\end{bmatrix}\).原来的基对应的坐标是 (1, 1), 过程表示为:
经过变换后新的向量是 1i'+1j'. 相对于新的基, 坐标仍然是 (1, 1), 但是相对于原来的基, 坐标变成1.(0, 1)+1.(-1, 0)=(-1, 1). 也就是说, 相对旧的基, 向量的坐标变了, 因此向量也变了, 而且逆时针旋转 90°

Same Vectors, Different Coordinates
如果向量不变, 但是用不同的基描述, 坐标会怎么变化?
仍然用上面举例. 旋转后的向量在新的基下的坐标和旋转前的向量在原来的基下的坐标一样, 都是 (1, 1). 而旋转后的向量在旧的基的向量是 (-1, 1), 因此 \(\bm{y} = A \bm{x}\) 还表示将同一个向量从新的基下的坐标转为原来的基的坐标, 如图:
那原来的基的坐标变成新的基会怎么变呢? 很简单: \(\bm{x} = A^{-1} \bm{y}\) 便实现将同一个向量的原来基的坐标转为新的基的坐标, 乘以 \(A^{-1}\) 就行了.

Transformation in Different Basis
矩阵/线性变换也是用坐标表示的!
对于旋转变换 \(A = \begin{bmatrix} 0 & -1 \\ 1 & 0 \\\end{bmatrix}\) 我们用原来的基表示 (比如说平面直角坐标系). 什么意思呢? 在原来的基下选了基向量, 并且用原来的基的坐标表示.
那么在一个新的基下, 这个线性变换怎么表示? 我们并不能直接将 (0, 1) 和 (-1, 0) 翻译成新的基的坐标, 因为这样只是"在原来的基选的基向量在新的基表示", 而不是"新的基选的基向量在新的基表示".
我们设 \(\bm{u}, \bm{v}\) 为变换前后新的基下的坐标. \(S\) 为新的基在原来的基下的坐标. 首先我们需要将新的基下的坐标转为原来的基的坐标. 于是有 \(\bm{u} \rightarrow S \bm{u}\). 接着在原来的基下线性变换, 得到原来的基下新的向量的坐标: \(S \bm{u} \rightarrow A S \bm{u}\). 接着将原来的基的坐标在转回新的基的坐标: \(A S \bm{u} \rightarrow S^{-1} A S \bm{u}\) 得到坐标 \(\bm{v}\)
因此:
这就是基变换公式.
Eigenvectors and Eigenvalues
特征值和特征向量的几何意义比较直白, 最初提到过. 就是说线性变换之后仍然保持在一条线的向量就是特征向量, 而 λ 代表 scale 的大小. 当然, 有的时候保证不了"一条线" (复特征值), 有的时候求出多个相同的特征值但是只有一个独立的特征向量.
Diagonalization
需要先介绍一下一个矩阵/线性变换的特征基 (Eigenbasis), 就是说基为线性变换 \(A\) 的特征向量 \(\bm{x}_1, \cdots , \bm{x}_n\), 也就是之前表示的 \(S\). 在这个新的基下, 线性变换 \(A\) 将会表示成 \(\Lambda\), 只是会将 \(\bm{x}_1\) scale \(\lambda_1\) 倍, \(\bm{x}_2\) scale \(\lambda_2\) 倍, 因此 \(\Lambda\) 一定是对角阵, 值代表特征值, 用图解释:
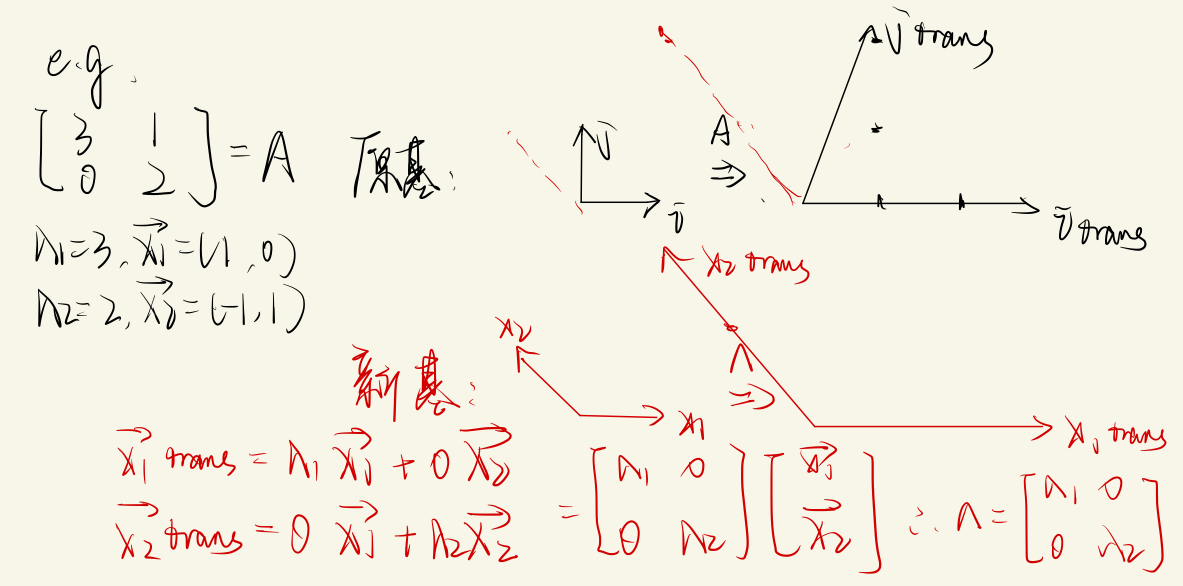
以自身特征基为基的线性变换是对角阵, 很方便. 组合多次线性变换的时候, 仅仅相当于让自身的基不断向着各自特征向量 \(\bm{x}_1\) 的 \(\lambda\) 倍 scale 即可, 也就是说让对角线的元素不断乘幂, 这正和之前从代数理解的角度一致.
接下来将会是最后一章内容了. 还会继续讲特征值和特征向量, 只不过关注对称矩阵了. 之后是 SVD 分解, 正式的线性变换 (线代本质) 以及一个应用伪逆的求解.

 摘要: reference的内容为唯一教程,接下来的内容仅为本人的课后感悟,对他人或无法起到任何指导作用。
摘要: reference的内容为唯一教程,接下来的内容仅为本人的课后感悟,对他人或无法起到任何指导作用。

