2.7 Cramer's Rule, Inverse Matrix and Volume 阅读笔记

行列式的应用和本质

reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。

Reference

1. Course website: Cramer's Rule, Inverse Matrix and Volume | Unit II: Least Squares, Determinants and Eigenvalues | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 20: Cramer’s rule, inverse matrix, and volume (mit.edu)
4. Extra Reading: Section 5.3 in Introduction to Linear Algebra, Fifth Edition by Gilbert Strang.
5. Extra videos (3Blue1Brown):
   1. The determinant | Chapter 6, Essence of linear algebra - YouTube

---

这一节讲了下行列式的两大应用：逆公式和Cramer法则。还提到了行列式的一个物理含义：线性变换前后 area scale 了多少。

Inverse

直接给出公式（lecture假装硬推2*2矩阵）：

\[\boldsymbol{A}^{-1}=\frac{\boldsymbol{C}^\mathrm{T}}{\det \boldsymbol{A}} \]

其中 C 为余子式矩阵 \(\begin{bmatrix} C_{11} & \cdots & C_{1n}\\ \vdots & \ddots & \vdots\\ C_{n1} & \cdots & C_{nn}\\ \end{bmatrix}\)。

证明：

\[\begin{align*} & \boldsymbol{A}\boldsymbol{A}^{-1}=\frac{\boldsymbol{A}\boldsymbol{C}^\mathrm{T}}{\det \boldsymbol{A}} \\ \Rightarrow & \boldsymbol{A}\boldsymbol{C}^\mathrm{T}=(\det\boldsymbol{A})\boldsymbol{I} \\ \Rightarrow & \begin{bmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & \ddots & \vdots\\ a_{n1} & \cdots & a_{nn}\\ \end{bmatrix}\begin{bmatrix} C_{11} & \cdots & C_{n1}\\ \vdots & \ddots & \vdots\\ C_{1n} & \cdots & C_{nn}\\ \end{bmatrix}=(\det\boldsymbol{A})\boldsymbol{I}\\ \Rightarrow & \text{diag}(\det\boldsymbol{A},\cdots,\det\boldsymbol{A})=(\det\boldsymbol{A})\boldsymbol{I}\\(\because&\sum_{j=1}^{n}a_{ij}C_{ij}=\det\boldsymbol{A},\quad\sum_{j=1}^{n}a_{ij}C_{kj}=0\quad\text{for }i\ne k) \end{align*} \]

最后一行的原因，第一个很显然，第二个为什么呢？我们任取一个矩阵，再让第i行的元素等于第k行得到新的矩阵，于是对原矩阵求 \(\sum_{j=1}^{n}a_{ij}C_{kj}\) 相当于求新矩阵按第 k 行展开的行列式 \(\sum_{j=1}^{n}a_{kj}C_{kj}\)，由于矩阵两行相等，行列式为零。

如果 A 行列式为零，则分母为零不可逆，对应之前的性质。

Why

很显然这么求逆得累死，为啥还要研究这个式子呢？因为这样可以从代数的角度研究了，比如如果对 A 进行某个元素的改变，那么如何描述 A 的逆的变化呢？有了公式才能研究。

Cramer's Rule

现在我们表示 \(\boldsymbol{Ax}=\boldsymbol{b}\) 的解：

\[\boldsymbol{x}=\boldsymbol{A}^{-1}\boldsymbol{b}=\frac{\boldsymbol{C}^\mathrm{T}\boldsymbol{b}}{\det \boldsymbol{A}} \]

研究 \(\boldsymbol{C}^\mathrm{T}\boldsymbol{b}\)：

\[\boldsymbol{C}^\mathrm{T}\boldsymbol{b}=\begin{bmatrix} C_{11} & \cdots & C_{n1}\\ \vdots & \ddots & \vdots\\ C_{1n} & \cdots & C_{nn}\\ \end{bmatrix}\begin{bmatrix} b_1\\\vdots\\b_n \end{bmatrix}=\begin{bmatrix} B_1\\\vdots\\B_n \end{bmatrix} \]

其中 \(B_j=\sum_{i=1}^{n}C_{ij}b_i=\boldsymbol{b}\text{ 替换 }\boldsymbol{A}\text{ 的第 }j\text{ 列的矩阵}\)

于是 \(x_i=\frac{\det\boldsymbol{B_i}}{\det \boldsymbol{A}}\)

同样，这个也只是给出一个理论的公式用于代数分析，实际上没人会用这个法则求解

Essence

3Blue1Brown 把接下来的应用（求面积/体积）当作行列式的本质——原area在线性变换后scale的程度。比如二维的话就是面积。

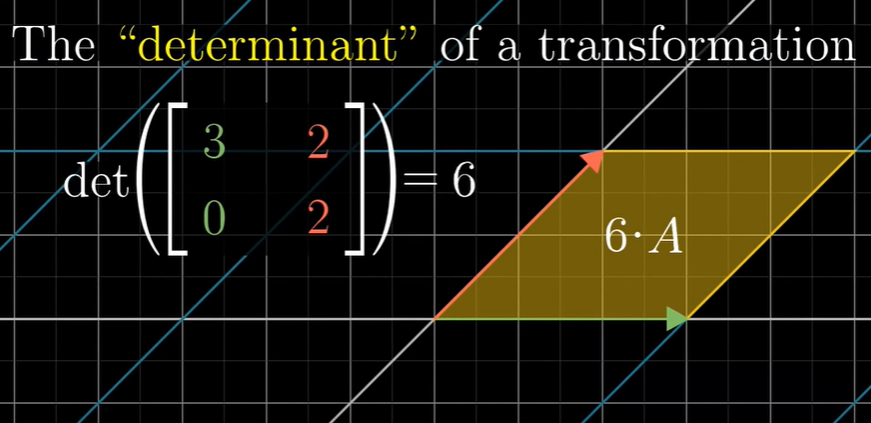
三维的也差不多，相当于求体积。

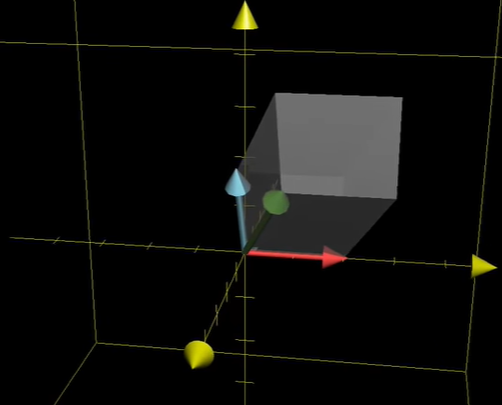
关于符号，如果变换后的基满足左手定则则为负，右手定则则为正。

如果行列式为零，则维度被压缩了，二维变成线，面积为零，三维变成面，体积为零。

再以二维为例看看行列式三个基本性质是否成立：

• 单位阵就是边长为1的正方形，面积为1，成立
• 互换行，手性变了，但面积大小仍然是一，因为还是那个图形
• 如果其中一条边伸长几倍，其余不变，则面积也扩大几倍

发现最后的相加性质不太好说明，直接贴一张图：

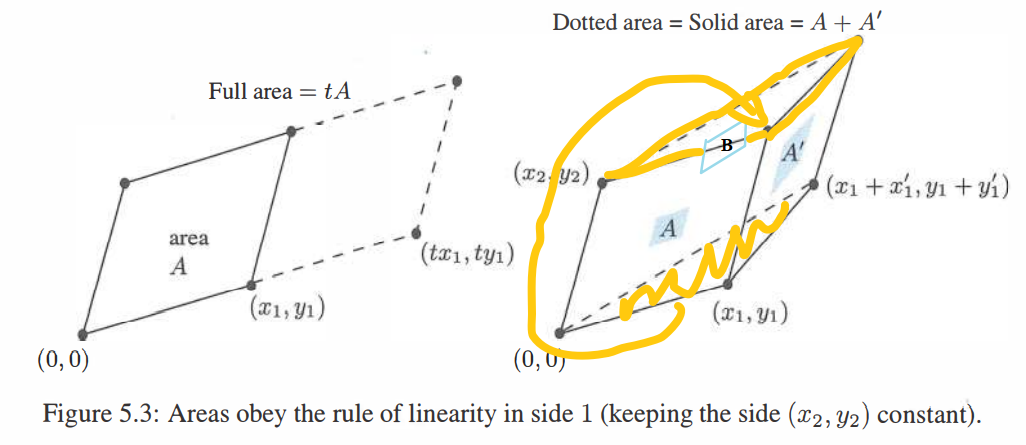
新平行四边形 B'（虚线框）的大小等于 A 的面积 + A' 的面积。