2.4 Orthogonal Matrices and Gram-Schmidt 阅读笔记

标准正交矩阵和标准正交化

reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。

Reference

1. Course website: Orthogonal Matrices and Gram-Schmidt | Unit II: Least Squares, Determinants and Eigenvalues | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 17: Orthogonal matrices and Gram-Schmidt (mit.edu)
4. Extra Reading: Section 4.4 in Introduction to Linear Algebra, Fifth Edition by Gilbert Strang.

---

本节开始说明怎么求出一个列空间的标准正交基，采用标准正交基会对投影和最小二乘公式的简化有很大的帮助。注意 A 的列向量是独立的。

标准正交向量：

\[\boldsymbol{q}_i^{\mathrm{T}}\boldsymbol{q}_j=\begin{cases} 0 & \text{ if } i\ne j \\ 1 & \text{ if } i=j \end{cases} \]

如果 i=j 时不恒为 1 且非零，那么仅仅是正交向量。

Orthonormal Matrices

设 Q 为一组标准正交向量组成的矩阵 \(\boldsymbol{Q}=\begin{bmatrix} \boldsymbol{q}_1 &\cdots &\boldsymbol{q}_n \end{bmatrix}\)，则有：

\[\boldsymbol{Q}^{\mathrm{T}}\boldsymbol{Q}=\begin{bmatrix} \boldsymbol{q}_1^{\mathrm{T}}\\ \vdots\\ \boldsymbol{q}_n^{\mathrm{T}} \end{bmatrix}\begin{bmatrix} \boldsymbol{q}_1 &\cdots &\boldsymbol{q}_n \end{bmatrix}=\begin{bmatrix} \boldsymbol{q}_1^{\mathrm{T}}\boldsymbol{q}_1 & \cdots & \boldsymbol{q}_1^{\mathrm{T}}\boldsymbol{q}_n\\ \vdots & \ddots & \vdots\\ \boldsymbol{q}_n^{\mathrm{T}}\boldsymbol{q}_1 & \cdots & \boldsymbol{q}_n^{\mathrm{T}}\boldsymbol{q}_n \end{bmatrix}=\boldsymbol{I} \]

我们管这种矩阵叫“标准正交矩阵”。

如果 Q 为方阵，则 \(\boldsymbol{Q}^{\mathrm{T}}=\boldsymbol{Q}^{-1}\)。此时的 Q 又被叫做正交矩阵 (Orthogonal Matrix)。

1.6 节有提到 \(\boldsymbol{P}^{-1}=\boldsymbol{P}^\mathrm{T}\)，其实置换矩阵也是正交矩阵的一种，当时推导这个关系还并没有用这个方法呢。但是还有很多不同类型的正交矩阵。比如 \(\begin{bmatrix} \cos\theta &-\sin\theta \\ \sin\theta &\cos\theta \end{bmatrix}\) 和 \(\frac{\sqrt{2}}{2}\begin{bmatrix} 1 &-1 \\1 &1 \end{bmatrix}\)。

Why Orthonormal Matrices?

为什么一定要用标准正交矩阵呢？

仔细想想便知，对 X^TX 求逆很麻烦，代入 X=Q 会发现 X^TX=I，逆也是 I，直接没了。这就大大简化了投影的公式！

设我们要投影到 \(\boldsymbol{Q}\) 的列空间，则投影方程为：

\[\boldsymbol{Q}^{\mathrm{T}}\boldsymbol{Q}\hat{\boldsymbol{x}}=\hat{\boldsymbol{x}}=\boldsymbol{Q}^{\mathrm{T}}\boldsymbol{b} \]

所以投影分量 \(\hat{x_i}=\boldsymbol{q}_i^{\mathrm{T}}\boldsymbol{b}\)。

投影矩阵为：

\[\boldsymbol{P}=\boldsymbol{Q}(\boldsymbol{Q}^{\mathrm{T}}\boldsymbol{Q})^{-1}\boldsymbol{Q}^\mathrm{T}=\boldsymbol{QQ}^{\mathrm{T}} \]

• 如果 Q 为方阵，则相当于投影到整个列空间，显然投影为自己，P=I，代数也可以推出来。
• 如果 Q 不是方阵，那 P ≠ I

但无论怎么说，有了标准正交矩阵，X^TX 永远消失了，太好了！那么怎么标准正交化呢？就要提出 Gram-Schmidt 正交化方法了。

Gram-Schmidt

Gram-Schmidt 正交化方法是对线性无关向量进行变换，求出其张成空间的标准正交基，其过程为：

线性无关向量 \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c},\cdots\) -> 正交向量 \(\boldsymbol{A},\boldsymbol{B},\boldsymbol{C},\cdots\) -> 标准正交向量 \(\boldsymbol{q}_1,\boldsymbol{q}_2,\boldsymbol{q_3},\cdots\)。

Orthogonal -> Orthonormal

这一步很简单：

\[\boldsymbol{q}_1=\frac{\boldsymbol{A}}{\left \| \boldsymbol{A} \right \|},\boldsymbol{q}_2=\frac{\boldsymbol{B}}{\left \| \boldsymbol{B} \right \|},\boldsymbol{q}_3=\frac{\boldsymbol{C}}{\left \| \boldsymbol{C} \right \|},\cdots \]

Independent -> Orthogonal

1. 假设只有一个向量。

   

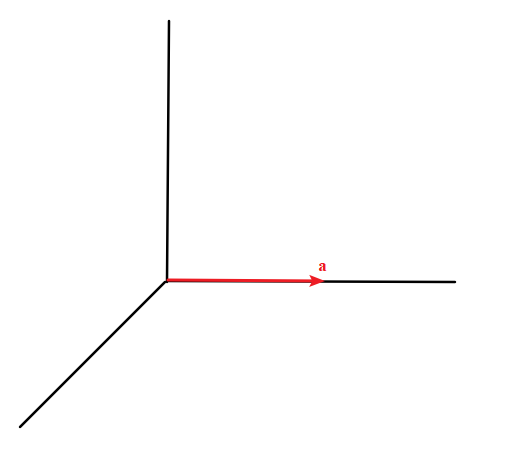
   则它自己构成正交向量组。

   \[\boldsymbol{A}=\boldsymbol{a} \]

2. 假设有两个向量，怎么找出一个和第一个向量正交的向量呢？让 b 在 A=a 上投影得到的误差向量！

   

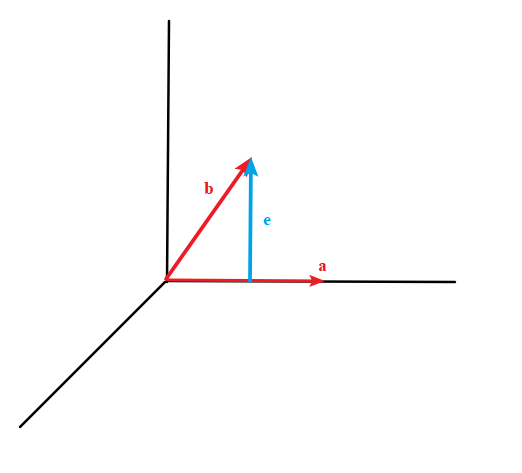
   则有：

   \[\boldsymbol{B}=\boldsymbol{e}=\boldsymbol{b}-\boldsymbol{Pb}=\boldsymbol{b}-\boldsymbol{A}\frac{\boldsymbol{A}^{\mathrm{T}}\boldsymbol{b}}{\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}} \]

3. 现在又来了第三个向量，怎么找出一个和前两个都正交的向量呢？

   

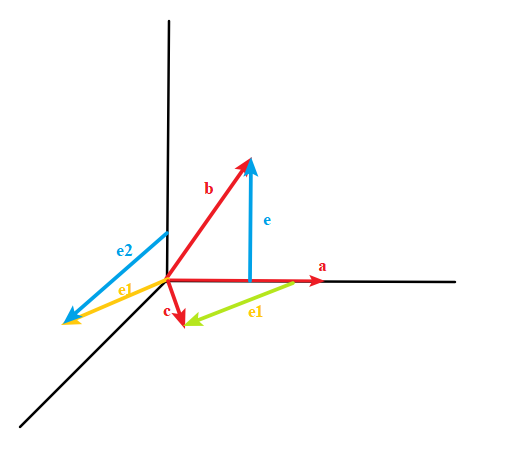
   先让 c 在 A=a 上投影得到投影向量，然后得到和 A 正交的误差向量 e₁，再让 e₁ 在 B=e 上投影得到和 B 正交的误差向量 e₂，这样获得的第三个向量和第一个与第二个都正交！

   实际上 e₁ 在 B=e 上投影等价于 c 在 B 上投影！于是有：

   \[\boldsymbol{C}=\boldsymbol{e}_2=\boldsymbol{e}_1-\boldsymbol{P}_2\boldsymbol{c}=\boldsymbol{c}-\boldsymbol{P}_1\boldsymbol{c}-\boldsymbol{P}_2\boldsymbol{c}=\boldsymbol{c}-\boldsymbol{A}\frac{\boldsymbol{A}^{\mathrm{T}}\boldsymbol{c}}{\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}}-\boldsymbol{B}\frac{\boldsymbol{B}^{\mathrm{T}}\boldsymbol{c}}{\boldsymbol{B}^{\mathrm{T}}\boldsymbol{B}} \]

4. 再来第四个向量就只需要让其和前三个向量正交，求其在前三个向量投影，剪掉这三个分量的投影向量，剩下的向量就和前三个向量正交了！以此类推后面的。

A=QR

用矩阵形式表示正交化，由于右乘矩阵代表列变换（矩阵右乘向量代表线性组合，因此右乘矩阵代表列变换，之前只提过左乘矩阵代表行变换），因此原矩阵 A 和正交矩阵 Q 之间可以用一个中间矩阵 R 来连接。

\[\boldsymbol{A}=\boldsymbol{Q}\boldsymbol{R} \]

为什么用这样的顺序呢？因为可以知道 R 是什么：

\[\boldsymbol{R}=\boldsymbol{Q}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A}=\begin{bmatrix} \boldsymbol{q}_1^{\mathrm{T}}\\ \vdots\\ \boldsymbol{q}_n^{\mathrm{T}} \end{bmatrix}\begin{bmatrix} \boldsymbol{a}_1 & \cdots & \boldsymbol{a}_n \end{bmatrix}=\begin{bmatrix} \boldsymbol{q}_1^{\mathrm{T}}\boldsymbol{a}_1 & \cdots & \boldsymbol{q}_1^{\mathrm{T}}\boldsymbol{a}_n\\ \vdots & \ddots & \vdots\\ \boldsymbol{q}_n^{\mathrm{T}}\boldsymbol{a}_1 & \cdots & \boldsymbol{q}_n^{\mathrm{T}}\boldsymbol{a}_n \end{bmatrix} \]

更奇妙的是，由于 Gram-Schmidt 中，

• q2 和 a(或者a1)=q1 正交。
• q3 和 a(或者a1)=q1，b(或者a2)=Linear_Combination(A,B也就是q1,q2) 正交。
• q4 和 a(或者a1)，b(或者a2)，c(或者a3) 正交
• ......

所以 R 为上三角矩阵，左下角全为0.

---

这一章真正整理的时候感觉很乱，发现很多概念都理解错了。比如没搞明白为什么 R 是个上三角阵，正交化方法是让原向量减去其在前面各个向量的投影（我理解成一种迭代的过程，用减掉第一个向量投影之后的误差向量继续往第二个向量投影，这样是可以的但是没法计算了，误差向量往第二个向量投影正等价于直接用原向量在第二个向量投影），以及标准正交化的大前提是对线性无关的向量操作，如果线性相关的话最小二乘法会有多解等等。所以感觉整理起来相当糟糕，今后也不知道回看还能不能看懂。