2.3 Projection Matrices and Least Squares 阅读笔记

投影矩阵和最小二乘法

reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。

Reference

1. Course website: Projection Matrices and Least Squares | Unit II: Least Squares, Determinants and Eigenvalues | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 16: Projection matrices and least squares (mit.edu)
4. Extra Reading: Section 4.3 in Introduction to Linear Algebra, Fifth Edition by Gilbert Strang. 和 常用的向量矩阵求导公式_TangowL-CSDN博客_向量求导法则

---

现在有几个问题仍未解决：

• 2.1 中为什么最后的两个结论成立？

  \[\boldsymbol{N}(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A})=\boldsymbol{N}(\boldsymbol{A})\\ \text{rank}(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A})=\text{rank}(\boldsymbol{A}) \]

• 最小二乘法的几何意义？

这一讲一边复习投影矩阵，一边详细解释最小二乘法，最后开一个标准正交基的概念。

Recap on Projection Matrices

我们都知道投影矩阵 \(\boldsymbol{P}=\boldsymbol{A}(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\)。

• \(\boldsymbol{b} \perp \boldsymbol{C}(\boldsymbol{A})\): 则 Pb 为零向量，投影只能投到一个点，就是零向量（因为起始点为原点）
• \(\boldsymbol{b} \in \boldsymbol{C}(\boldsymbol{A})\): 则 Pb = b，投影就是自己

这些是从几何意义来看的，代数上：

• \(\boldsymbol{b} \perp \boldsymbol{C}(\boldsymbol{A})\): \(\boldsymbol{A}(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\boldsymbol{b}=\boldsymbol{A}(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}(\boldsymbol{A^{\mathrm{T}}}\boldsymbol{b})=\boldsymbol{0}\)，因为 b ∈ N(A^T) ⊥ C(A)
• \(\boldsymbol{b} \in \boldsymbol{C}(\boldsymbol{A})\): \(\boldsymbol{A}(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\boldsymbol{b}=\boldsymbol{A}(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{A}((\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}(\boldsymbol{A^{\mathrm{T}}}\boldsymbol{A}))\boldsymbol{x}=\boldsymbol{Ax}=\boldsymbol{b}\)

向量 p + e = b，p 在 A 的列空间里，投影矩阵为 P，而 e 在 A 的什么空间呢？左零空间，因为 e 和 C(A) 正交。那么把 p 投影到 A 的左零空间得到的投影向量便是 e 了，对应的投影矩阵是什么？

• \(\boldsymbol{e}=\boldsymbol{b}-\boldsymbol{p}=\boldsymbol{b}-\boldsymbol{Pb}=(\boldsymbol{I}-\boldsymbol{P})\boldsymbol{b}\)，故 P' = I-P

Least Squares

上一节我们已经知道了怎么用投影的方式拟合直线了，还算出结果来了。

整个过程是：

• 找出拟合直线系数 \(\hat {\boldsymbol{x}}\) 和投影向量 \(\boldsymbol{p}\) 。
• 使得 \(\boldsymbol{A}^\mathrm{T}\boldsymbol{b}=\boldsymbol{A}^\mathrm{T}\boldsymbol{A}\hat {\boldsymbol{x}}\)，解出 \(\hat {\boldsymbol{x}}\) 和 \(\boldsymbol{p}=\boldsymbol{A}\hat {\boldsymbol{x}}\)。

为什么用投影的方式 \(\boldsymbol{A}^\mathrm{T}\boldsymbol{b}=\boldsymbol{A}^\mathrm{T}\boldsymbol{A}\hat {\boldsymbol{x}}\) 解不可解方程叫做 Least Squares 呢？

先给出 Least Squares 名字的由来：给定不可解方程 \(\boldsymbol{Ax}=\boldsymbol{b}\)，求出 x 使误差的平方和最小，也就是误差向量 e 的模的平方最小。误差是数据点到拟合曲线纵坐标的差（并不是距离！虽然只是差个系数）

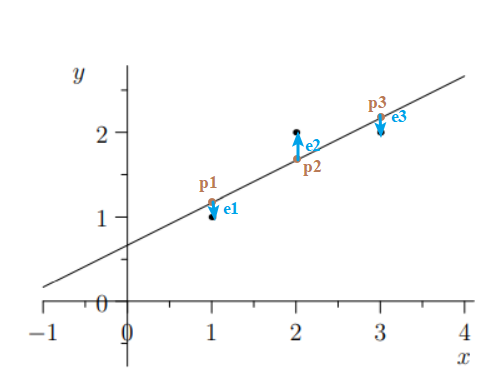
也就是说求：

\[\underset{\boldsymbol{x}}{\arg\min}\left \| \boldsymbol{A}\boldsymbol{x}-\boldsymbol{b} \right \|^{2} \]

如果 \(\underset{\boldsymbol{x}}{\arg\min}\left \| \boldsymbol{A}\boldsymbol{x}-\boldsymbol{b} \right \|^{2}=\hat{\boldsymbol{x}}=(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\)，便能解释了。本节给出两个角度证明，我又用矩阵求导的角度算了一下，放在附录了 (懒得敲公式了而且这种纯算数的东西有什么意义吗？)。

Geometry

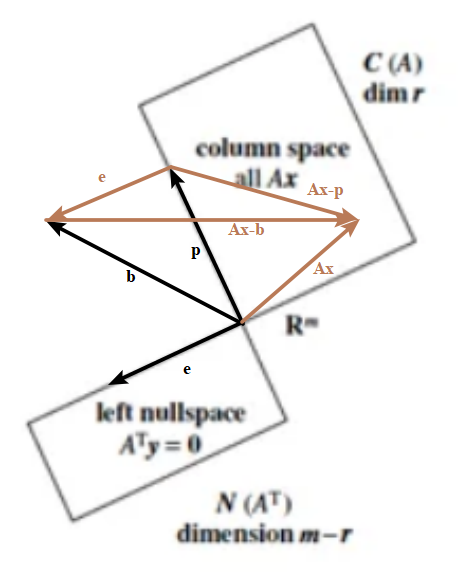
Ax 是 列空间任意向量，注意看绿色的三个向量 e，Ax-b，Ax-p，构成直角三角形，因为 e 在左零空间，和在列空间的 Ax-p 是正交的。因此 Ax-b 向量的模相当于直角三角形的斜边了，几何上，只有 Ax-b 垂直于 C(A)，模才最短。

代数上 \(\underset{\boldsymbol{x}}{\arg\min}\left \| \boldsymbol{A}\boldsymbol{x}-\boldsymbol{b} \right \|^{2}=\underset{\boldsymbol{x}}{\arg\min}(\left \| \boldsymbol{A}\boldsymbol{x}-\boldsymbol{p} \right \|^{2}+\left \| \boldsymbol{e} \right \|^{2})\)。因此 x 为 满足 Ax=p 的 x。所以 \(\boldsymbol{x}=\hat{\boldsymbol{x}}\)。此时的误差正好等于投影向量与原向量的误差。

Derivative

已经有：

\[\begin{matrix}C &+ &D &= &1 \\C &+ &2D &= &2 \\C &+ &3D &= &2 \end{matrix} \]

于是

\[\begin{matrix} & \underset{\boldsymbol{x}}{\arg\min}\left \| \boldsymbol{A}\boldsymbol{x}-\boldsymbol{b} \right \|^{2}\\ = & \underset{C,D}{\arg\min}\{(C+D-1)^{2}+(C+2D-2)^{2}+(C+3D-2)^{2}\}\\ = & \underset{C,D}{\arg\min}f(C,D) \end{matrix} \]

对 f 求 C 和 D 的偏导得：

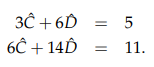
正好和：

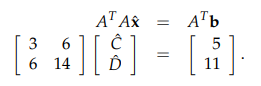
一致。

Matrix Derivative

略。

Drawback

线性拟合会受到异常数据点/离群量 (outlier) 干扰，导致和理论得直线偏差过大。

此外很多问题是非线性的，怎么能用直线拟合？

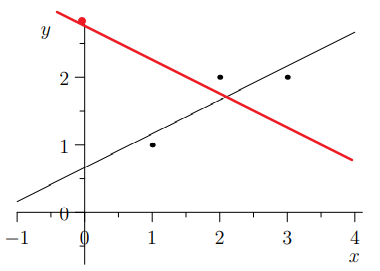
Prove \(\boldsymbol{A}^\mathrm{T}\boldsymbol{A}\) Properties

\[\boldsymbol{N}(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A})=\boldsymbol{N}(\boldsymbol{A})\\ \text{rank}(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A})=\text{rank}(\boldsymbol{A}) \]

• 需要证明 \(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}\) 的解空间和 \(\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}\) 一致。也就是说证明 \(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}\Rightarrow\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}\)。

  \[\begin{matrix} &\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} \\\Rightarrow &\boldsymbol{x}^{\mathrm{T}}\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} \\\Rightarrow &(\boldsymbol{A}\boldsymbol{x})^{\mathrm{T}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} \\\Rightarrow &\left \| \boldsymbol{Ax} \right \|^{2}=\boldsymbol{0} \\\Rightarrow &\boldsymbol{Ax}=\boldsymbol{0} \end{matrix} \]

• 零空间都一样，故 dim 一样，r = n - dim 且 n 一样，故 r 一样。

• 然后利用第二条就能证明 A 列满秩 A^TA 方阵可逆。

为什么可以用最小二乘法，可以用公式 \(\hat{\boldsymbol{x}}=(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\) 来求 Ax=b 的近似解？大前提就是 A^TA 方阵可逆，A 列满秩。

Dependent Columns

如果不满足呢？举个例子：

显然 C+Dt 无法表示一个垂直 t 轴的直线，因此无法穿过 (1,1) 和 (1,3)。为了使拟合直线距离两个点在 t=1 的误差最小，显然需要穿过 (1,2) 这个点，但是这会有无穷多的解。学了伪逆之后我们会有一个从这些解中选择的基准。接下来，还是讨论如果 A 的列向量独立的情况吧。

Orthonormal Vectors

其实一组相互正交的单位向量可以作为一组基，一定是独立的，称为标准正交向量 (Orthonormal Vectors)，它们可以构成标准正交基。下一讲我们会说明如果对列向量独立的矩阵 A 求出其列空间标准正交基，并说明这样做的好处.