2.2 Projections onto Subspaces 阅读笔记

投影

reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。

Reference

1. Course website: Projections onto Subspaces | Unit II: Least Squares, Determinants and Eigenvalues | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 15: Projections onto subspaces (mit.edu)

---

这一讲来解释为什么上一讲里面解求 \(\boldsymbol{Ax}=\boldsymbol{b}\) 的近似解要变成 \(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}\hat{\boldsymbol{x}}=\boldsymbol{A}^{\mathrm{T}}\boldsymbol{b}\)。这里涉及了投影 (Projection) 的概念，因此需要解释一下。

首先先回顾一下最熟悉的平面直角坐标系下的投影。

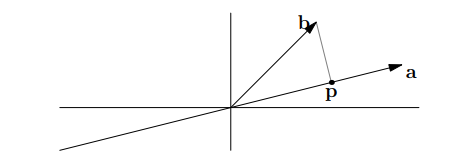
a 是二维空间中过原点的一个 subspace，想求直线上距离 b 点最近的点，显然需要作垂线得到垂足 p，即为最近的点。此时向量 p 就是向量 b 在子空间直线上的投影。

高中的时候要求投影向量 p 的话印象里是先 \(\left || \boldsymbol{b} \right ||\cos\theta\cdot\frac{\boldsymbol{a}}{\left || \boldsymbol{a} \right ||}\)，相当于投影向量的模乘 a 方向的单位向量。上下同乘 a 的模得到：

\[\frac{\left || \boldsymbol{a} \right ||\left || \boldsymbol{b} \right ||\cos\theta}{\left || \boldsymbol{a} \right ||}\cdot\frac{\boldsymbol{a}}{\left || \boldsymbol{a} \right ||}=\frac{\boldsymbol{a}\cdot\boldsymbol{b}}{\left || \boldsymbol{a} \right ||}\cdot\frac{\boldsymbol{a}}{\left || \boldsymbol{a} \right ||} \]

三角函数看起来总是不那么简洁，这一节将用矩阵的形式来阐述投影，同样从二维开始。再解释求近似解和投影的关系，最后给出一般性的投影公式和最小二乘法简单应用。

Two Dimension

此时有一个误差向量 e，方向从 p 到 b，e=b-p。

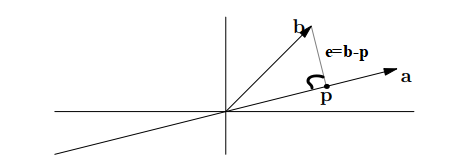
这里体现出了正交性，e ⊥ a，即：

\[\boldsymbol{a}^\mathrm{T}(\boldsymbol{b}-\boldsymbol{p})=0 \]

设 \(\boldsymbol{p}=\boldsymbol{a}\hat x\)，则有：

\[\boldsymbol{a}^\mathrm{T}(\boldsymbol{b}-\boldsymbol{a}\hat x)=0\\ \Rightarrow\boldsymbol{a}^\mathrm{T}\boldsymbol{b}=\boldsymbol{a}^\mathrm{T}\boldsymbol{a}\hat x \]

因此有：

\[\hat x=\frac{\boldsymbol{a}^\mathrm{T}\boldsymbol{b}}{\boldsymbol{a}^\mathrm{T}\boldsymbol{a}}\text{, }\boldsymbol{p}=\boldsymbol{a}\cdot\frac{\boldsymbol{a}^\mathrm{T}\boldsymbol{b}}{\boldsymbol{a}^\mathrm{T}\boldsymbol{a}} \]

其实和上面的高中版本等价。

分析这个式子发现 a 在给定直线的时候任取直线内一点（一个向量），p 都是不会变的，因为就相当于给原来的 a 加个系数，上下同乘系数的平方，消了，不过 b 要是数乘一个倍数投影向量 p 也会同乘相同系数。这说明投影向量只和被投影的向量 b 和 给的直线有关，和直线内的向量 a 无关。

Projection Matrix

对 p 进行一下结合律：

\[\boldsymbol{p}=\boldsymbol{a}\cdot\frac{\boldsymbol{a}^\mathrm{T}\boldsymbol{b}}{\boldsymbol{a}^\mathrm{T}\boldsymbol{a}}=\frac{\boldsymbol{a}\boldsymbol{a}^\mathrm{T}}{\boldsymbol{a}^\mathrm{T}\boldsymbol{a}}\boldsymbol{b}=\boldsymbol{Pb} \]

于是有：

\[\boldsymbol{P}=\frac{\boldsymbol{a}\boldsymbol{a}^\mathrm{T}}{\boldsymbol{a}^\mathrm{T}\boldsymbol{a}} \]

为投影矩阵。

这个矩阵有什么性质呢？

• \(\boldsymbol{P}^\mathrm{T}=\boldsymbol{P}\)：显然。
• \(\text{rank}(\boldsymbol{P})=1\)：1.12 中已经提到，列向量乘行向量会得到秩 1 矩阵，此外 P 的列空间是什么呢？列向量的线性组合的张成空间，即 Pb 的张成空间，也就是投影向量 p 所在的空间了，是直线啊，维度为1因此秩为1.
• \(\boldsymbol{P}^2=\boldsymbol{P}\)：因为对一个向量往一条直线上投影两次和投影一次是一样的啊。

Why Project?

为什么要投影呢，这和求 \(\boldsymbol{Ax}=\boldsymbol{b}\) 的近似解有关系。

为什么 \(\boldsymbol{Ax}=\boldsymbol{b}\) 无解？因为 \(\boldsymbol{b}\) 不在 \(\boldsymbol{A}\) 的列空间。

如果把 \(\boldsymbol{b}\) 投影到 \(\boldsymbol{A}\) 的列空间得到 \(\boldsymbol{p}\)，就可以解近似的方程 \(\boldsymbol{A}\hat{\boldsymbol{x}}=\boldsymbol{p}\) 了，怎么求 p 呢？涉及到高维空间的投影了，下面来研究。

Higher Dimensions

以 3 维为例推导公式。

假设我们要求三维空间的一个向量 b 在二维平面上一个投影 p，二维平面有两个基向量 a₁，a₂。看起来像这样：

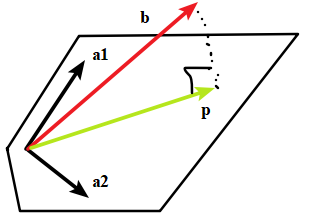
这个平面便是 \(\boldsymbol{A}=\begin{bmatrix} \boldsymbol{a}_1 & \boldsymbol{a}_2 \end{bmatrix}\) 的列空间。

仍然有 e ⊥ a_i，i = 1 和 2，即：

\[\boldsymbol{a}_1^\mathrm{T}(\boldsymbol{b}-\boldsymbol{p})=0\\ \boldsymbol{a}_2^\mathrm{T}(\boldsymbol{b}-\boldsymbol{p})=0 \]

用矩阵形式合并得：

\[\boldsymbol{A}^\mathrm{T}(\boldsymbol{b}-\boldsymbol{p})=0 \]

这里设 \(\boldsymbol{p}=\boldsymbol{a}_1\hat x_1+\boldsymbol{a}_2\hat x_2=\boldsymbol{A}\hat {\boldsymbol{x}}\)，于是有：

\[\boldsymbol{A}^\mathrm{T}(\boldsymbol{b}-\boldsymbol{A}\hat {\boldsymbol{x}})=0\\ \Rightarrow \boldsymbol{A}^\mathrm{T}\boldsymbol{b}=\boldsymbol{A}^\mathrm{T}\boldsymbol{A}\hat {\boldsymbol{x}}=\boldsymbol{A}^\mathrm{T}\boldsymbol{p} \]

这时我们发现向量 e 的空间就是 A 的左零空间，即 \(\boldsymbol{e}\in\boldsymbol{N}(\boldsymbol{A}^\mathrm{T})\)，我们已经知道了左零空间与列空间正交，因此向量 e 也与列空间正交，这和我们的直观是对应的。

上一讲提到 \(\text{rank}(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A})=\text{rank}(\boldsymbol{A})\)，这里已经假设了 a₁ 和 a₂ 是二维平面的基，因此独立，A 列满秩，因此 \(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A}\) 可逆，故得 \(\hat {\boldsymbol{x}}\)：

\[\hat{\boldsymbol{x}}=(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\boldsymbol{b}\text{, }\boldsymbol{p}=\boldsymbol{A}(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\boldsymbol{b}=\boldsymbol{Pb} \]

投影矩阵 P：

\[\boldsymbol{P}=\boldsymbol{A}(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}} \]

如果 A 是可逆方阵，\(\boldsymbol{p}=\boldsymbol{a}_1\hat x_1+\boldsymbol{a}_2\hat x_2=\boldsymbol{A}\hat {\boldsymbol{x}}\)，向量 p 所在空间为整个空间，说明向量 b 被投影到整个空间，那也就是它自己了，Pb=b，一计算此时P=I。但是通常 A 不是方阵，根本不可逆。

给出两点比较容易证的性质：

• \(\boldsymbol{P}^\mathrm{T}=\boldsymbol{P}\)
• \(\boldsymbol{P}^2=\boldsymbol{P}\)

Least Squares Fitting A Line

现在来简单应用一下投影——最小二乘法，我们经常需要拟合直线：

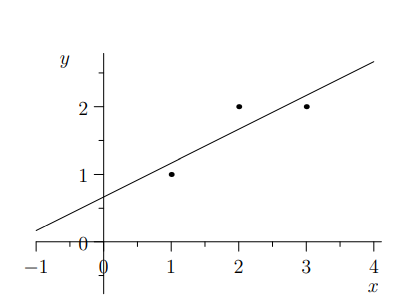
三个点坐标 (1,1) (2,2) (3,2) 显然不在一条直线上。

可以用 \(y=C+Dx\) 拟合，因此需要解方程：

\[\begin{matrix}C &+ &D &= &1 \\C &+ &2D &= &2 \\C &+ &3D &= &2 \end{matrix} \]

表示成 \(\boldsymbol{Ax}=\boldsymbol{b}\) 显然无解：

\[\begin{bmatrix} 1 &1 \\1 &2 \\1 &3 \end{bmatrix}\begin{bmatrix} C\\D \end{bmatrix}=\begin{bmatrix} 1\\2 \\2 \end{bmatrix} \]

于是需要把 b 投影到 A 的列空间得到投影向量 p，解 \(\boldsymbol{A}\hat{\boldsymbol{x}}=\boldsymbol{p}\) 即 \(\boldsymbol{A}^\mathrm{T}\boldsymbol{A}\hat {\boldsymbol{x}}=\boldsymbol{A}^\mathrm{T}\boldsymbol{b}=\boldsymbol{A}^\mathrm{T}\boldsymbol{p}\)

得 \(\hat{\boldsymbol{x}}=(\boldsymbol{A^{\mathrm{T}}\boldsymbol{A}})^{-1}\boldsymbol{A^{\mathrm{T}}}\boldsymbol{b}=\begin{bmatrix} \frac{2}{3}\\\frac{1}{2} \end{bmatrix}\)

因此拟合直线：\(y=\frac{2}{3}+\frac{1}{2}x\)。