2.1 Orthogonal Vectors and Subspaces 阅读笔记

正交向量和正交空间

reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。

Reference

1. Course website: Orthogonal Vectors and Subspaces | Unit II: Least Squares, Determinants and Eigenvalues | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 14: Orthogonal vectors and subspaces (mit.edu)

---

Unit 1 研究维度

Unit 2 研究正交性

Unit 3 研究基

现在开始研究正交性了。

Big Picture

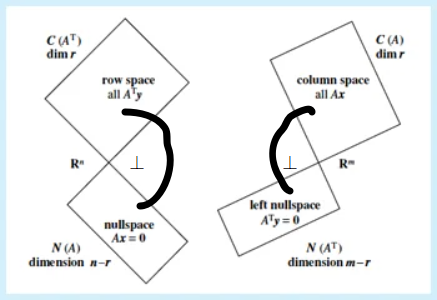
重新亮出这个 big picture，它还包含一层意思：A 的行空间和零空间相互正交，A 的列空间和左零空间相互正交。\(\R^n\) 和 \(\R^m\) 都被分割成了相互正交的空间。

接下来开始详细说明，在此之前需要先解释正交的概念。

Orthogonal Vectors

向量的正交即为垂直，也就是：

\[\boldsymbol{x}\cdot\boldsymbol{y}=0 \]

对向量的内积可以表示成一个行向量矩阵乘一个列向量，而且内积可以相互交换顺序，也就是：

\[\boldsymbol{x}\cdot\boldsymbol{y}=\boldsymbol{x}^\mathrm{T}\boldsymbol{y}=\boldsymbol{y}^\mathrm{T}\boldsymbol{x}=\boldsymbol{y}\cdot\boldsymbol{x} \]

勾股定理可以表示为：

\[{\left \| \boldsymbol{x} \right \|}^{2}+{\left \| \boldsymbol{y} \right \|}^{2}={\left \| \boldsymbol{x}+\boldsymbol{y} \right \|}^{2} \]

和向量正交之间可以相互推导，因为：

\[\begin{matrix} &\left \| \boldsymbol{x} \right \|^{2}+\left \| \boldsymbol{y} \right \|^{2}=\left \| \boldsymbol{x}+\boldsymbol{y} \right \|^{2}\\\Leftrightarrow &\boldsymbol{x}^{\mathrm{T}}\boldsymbol{x}+\boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}=(\boldsymbol{x}+\boldsymbol{y})^{\mathrm{T}}(\boldsymbol{x}+\boldsymbol{y}) \\\Leftrightarrow &\boldsymbol{x}^{\mathrm{T}}\boldsymbol{x}+\boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}=(\boldsymbol{x}^{\mathrm{T}}+\boldsymbol{y}^{\mathrm{T}})(\boldsymbol{x}+\boldsymbol{y}) \\\Leftrightarrow &\boldsymbol{x}^{\mathrm{T}}\boldsymbol{y}+\boldsymbol{y}^{\mathrm{T}}\boldsymbol{x}=0 \\\Leftrightarrow &2\boldsymbol{x}^{\mathrm{T}}\boldsymbol{y}=0 \\\Leftrightarrow &\boldsymbol{x}^{\mathrm{T}}\boldsymbol{y}=0 \\\Leftrightarrow &\boldsymbol{x}\cdot\boldsymbol{y}=0 \end{matrix} \]

Orthogonal Subspaces

若子空间 \(S\) 与 \(T\) 正交 (Orthogonal)，则有：

\[\forall \boldsymbol{x}\forall \boldsymbol{y}(\boldsymbol{x}\in S,\boldsymbol{y}\in T,\boldsymbol{x}^{\boldsymbol{\mathrm{T}}}\boldsymbol{y}=0\rightarrow S\perp T) \]

注意平面垂直和平面代表的子空间正交完全不是一个概念：两个垂直的平面不是正交的。

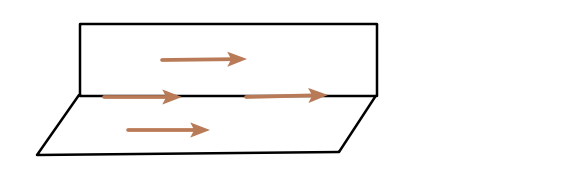
平面垂直只和法线有关，而且维度必须一样（二维），但是空间正交不一定同纬度（三维空间过原点的平面和过原点的平面法线是正交的，两个过原点相互垂直的线也是正交的，原点和任何子空间都是正交的）。

C(A^T) ⊥ N(A)

下面便开始简单证明了。

Sloppy Proof

首先是行空间正交于零空间：

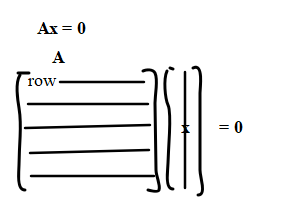
这是因为 Ax=0 本身意味着 A 的所有行向量和向量 x 的内积都是 0. 因此 x 和 A 的行向量的任意线性组合得到的向量内积也是 0. 因此 x 和 A 的行空间内任意向量正交。而 x 是 A 的零空间的任意向量，因此行空间正交于零空间。

同理列空间正交于左零空间，只需要代入 A:=A^T 即可。

Orthogonal Complements

行空间不仅正交于零空间，而且他们的维度相加等于 n，也就是整个空间。

在 \(\R^3\) 中，可以出现两个子空间的维度相加不等于整个空间的维度。比如两个过原点垂直的直线相互正交，维度和却为 2。

但是行空间和零空间的维度和却是整个空间！而且他们是相互正交的，因此：

• \(\boldsymbol{C}(\boldsymbol{A}^\mathrm{T})\) 和 \(\boldsymbol{N}(\boldsymbol{A})\) 互为 (\(\R^n\) 的) 正交补 (Orthogonal Complements)，同理：

• \(\boldsymbol{C}(\boldsymbol{A})\) 和 \(\boldsymbol{N}(\boldsymbol{A}^\mathrm{T})\) 互为 (\(\R^n\) 的) 正交补。

"Solve" Ax=b when there's no solution

我们不可避免需要解一些无解的线性方程，通常方程数量大于未知数的数量，即 \(m>n\)。

比如假设“房价” \(y\) 为“距离市中心距离” \(a_1\)，“大小” \(a_2\)，“年份” \(a_3\)，“楼层数” \(a_4\) 的线性函数，我们想要建模知道权重系数是多少，即给定 \(a_i\) 去求解 \(y=x_1a_1+x_2a_2+x_3a_3+x_4a_4\) 的系数 \(x_i\)。

理论上只需要知道 4 组 \({a_i}\) 和 4 组 \(y\) 就能唯一求出 \({x_i}\) 了，但实际总会存在各种误差导致测量的数据并不能严格满足理论的函数，因此就会测量很多组数据，出现 \(m>n\)，导致无解。所以怎么办呢？

• 扔掉数据点？不行啊，每个数据点可能都有误差，你在不知道理论模型是什么的情况下怎么知道要扔掉哪个数据点呢？相反初高中的学习早就让我们知道多次测量才能减小误差，单次实验具有偶然性。
• 管他可不可解直接消元法？也不行，消元法仅能用于可解的线性方程。

真正的做法是把 \(\boldsymbol{Ax}=\boldsymbol{b}\) 变成 \(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}\hat{\boldsymbol{x}}=\boldsymbol{A}^{\mathrm{T}}\boldsymbol{b}\)。这时获得一个重要的矩阵：\(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}\)，它是方阵而且是对称的，下一节会详细说明。

\(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}\) 和 \(\boldsymbol{A}\) 有着密不可分的关系，直接给出两个结论：

\[\boldsymbol{N}(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A})=\boldsymbol{N}(\boldsymbol{A})\\ \text{rank}(\boldsymbol{A}^{\boldsymbol{\mathrm{T}}}\boldsymbol{A})=\text{rank}(\boldsymbol{A}) \]

此方阵何时可逆？大小 n by n，所以秩必须是 n 才可逆，所以 A 的秩必须也是 n，也就是说 A 列满秩，列向量线性无关。