1.13 Graphs, Networks, Incidence Matrices 阅读笔记

图和关联矩阵

reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。

Reference

1. Course website: Graphs, Networks, Incidence Matrices | Unit I: Ax = b and the Four Subspaces | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 12: Graphs, networks, incidence matrices (mit.edu)

---

线性代数有很多应用，比如机器学习中的数据的存储就需要矩阵和线性代数的知识，而图网络的存储也需要矩阵和线性代数的知识。本节讲的就是线性代数在图当中的应用（实际场景选用电路），分析两个零空间辅以得出一个欧拉公式。

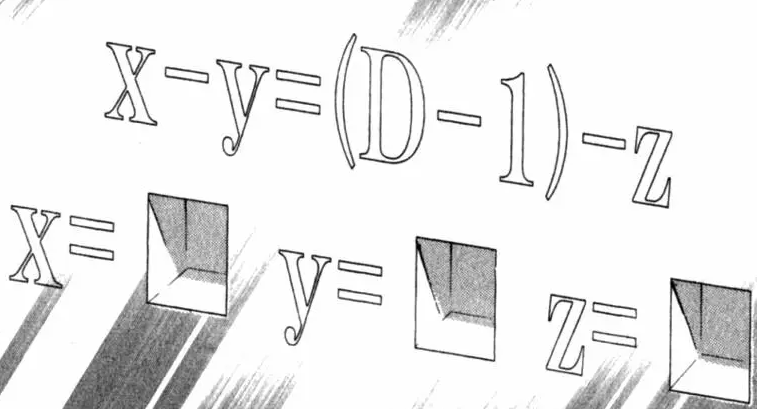
Definition of Graphs

绝大多数情况人们都把图视作边和点的集合。\(\mathcal{G}=\{\mathcal{V},\mathcal{E}\}\)。

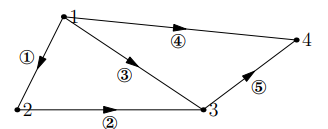
设 \(n\) 为节点个数，\(m\) 为边的个数。本节举例 \(n=4\) 和 \(m=5\)，并为边和点表上序号。

图可以是有向的和无向的，区别就在于有没有箭头。本节举例为有向图。

Incidence Matrix

关联矩阵 (Incidence Matrix) 用来描述边和节点的关系。和邻接矩阵 (Adjacency Matrix) 不同，关联矩阵一行代表一条边，一列代表一个节点，一行中仅源节点 (Source Node) 和目标节点 (Target Node) 有非零值 -1 和 +1，其余全为零。而邻接矩阵每一行每一列都代表一个节点，如果从第 i 个节点出发到第 j 个节点有边，就在 i 行 j 列赋值为 1，否则为 0.

本节研究关联矩阵，上图的关联矩阵表示为：

\[\boldsymbol{A}=\begin{bmatrix} -1 & 1 &0 &0 \\0 &-1 &1 &0 \\-1 &0 &1 &0 \\-1 &0 &0 &1 \\0 &0 &-1 &1 \end{bmatrix} \]

去掉箭头，如果几条边围成了一个圈 (而且圈里面不能有其他的圈)，那就成环 (Loop) 了，这个图的前三条边成环了和后三条边成环了，对应前三行和后三行，以后三行举例：

\[\boldsymbol{A}_\text{后三行}=\begin{bmatrix} -1 &0 &1 &0 \\-1 &0 &0 &1 \\0 &0 &-1 &1 \end{bmatrix} \]

观察这个矩阵的第一行和第三行相加正好等于第二行，所以这个矩阵的行向量是线性相关的。这还说明了原图从 3 号边到 5 号边的结果和走 4 号边是一样的。给出结论回路的行向量是线性相关的。

同时我们发现关联矩阵是相当稀疏的，每行只有两个元素非零。所以很多情况下都会压缩矩阵成一个 m 行 2 列的矩阵。每行第一个元素为源节点序号，第二个元素为目标节点序号。

Nullspace

来研究矩阵 A 的零空间，需要解 \(\boldsymbol{Ax}=\boldsymbol{0}\)：

\[\boldsymbol{Ax}=\begin{bmatrix}x_{2}-x_{1} \\x_{3}-x_{2} \\x_{3}-x_{1} \\x_{4}-x_{1} \\x_{4}-x_{3} \end{bmatrix}=\begin{bmatrix}0 \\0 \\0 \\0 \\0 \end{bmatrix} \]

\(\boldsymbol{x}\) 代表了势 (potential)，在电路中就是电势。\(\boldsymbol{Ax}=\boldsymbol{0}\) 代表了电势差为0.

显然只有等电势的时候电势差才为零 (这是连通图)，因此 \(x_1=x_2=x_3=x_4\)，\(\boldsymbol{x}=c(1,1,1,1)\)，基只有一个向量，因此只有一个自由变量，\(n-r=1\)。任意一个节点且仅一个节点为自由变量。

联系物理角度，一旦给这样一个电路图（只有导线和节点）接地（给一个自由变量赋值），那么所有节点电势全都为零（所有变量的值可以唯一确定）。

Left Nullspace

来研究矩阵 A 的左零空间，需要解 \(\boldsymbol{A}^\mathrm{T}\boldsymbol{y}=\boldsymbol{0}\)：

\[\boldsymbol{A}^\mathrm{T}\boldsymbol{y}=\begin{bmatrix}-1 &0 &-1 &-1 &0 \\1 &-1 &0 &0 &0 \\0 &1 &1 &0 &-1 \\0 &0 &0 &1 &1 \end{bmatrix}\begin{bmatrix}y_1 \\y_2 \\y_3 \\y_4 \\y_5 \end{bmatrix}=\left\{\begin{matrix}-y_1 & &-y_3 &-y_4 & &=0 \\+y_1 &-y_2 & & & &=0 \\ &+y_2 &+y_3 & &-y_5 &=0 \\ & & &+y_4 &+y_5 &=0 \end{matrix}\right. \]

再放出这个图：

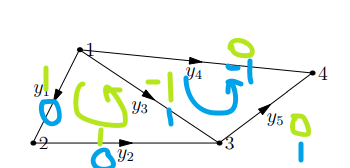
显然这是基尔霍夫电流定律 (Kirchhoff’s Current Law, KCL) (这个“显然”有点不要脸了，只是因为我学过电路罢了...)。每个节点流入为正，流出为负。也就是说左零空间是要我求出一组可能的电流值 (每条边)。

这个方程有 special solutions 吗？这个矩阵满秩吗？联想到刚刚提到的 loop 的概念，原矩阵行向量线性相关，因此转置后矩阵的列向量不是独立的，因此一定有非零解。

怎么求呢？当然可以 reduced echelon form，但是这样就看不懂物理意义了。

我们可以让每个回路的边有电流，回路之外的边没有电流，顺着方向走的电流为1，反着为0，这样就有非零值电流了，而且满足KCL，比如这个图里面有两个回路，因此有两组 special solutions：

直接给出结论：满足 KCL 的回路电流的 special solutions 的个数正为回路的个数。

因此解 \(y=c1(1,1,-1,0,0)+c2(0,0,1,-1,1)\)。基的个数等于回路的个数。

题外话：什么情况下矩阵 A 的行向量是线性无关的呢？那就是 A^T 的列向量线性无关，左零空间的基的个数为0，回路的个数为0，什么样的图没有回路呢？哦原来是树 (Tree) 啊。

Euler's Formular

已知 \(\dim\boldsymbol{N}(\boldsymbol{A}^\mathrm{T})=\#\text{ loops}=m-r\)，其中 \(m=\#\text{ edges}\)。

又已知 \(\dim\boldsymbol{N}(\boldsymbol{A})=n-r=1\Rightarrow r=n-1\)，其中 \(n=\#\text{ nodes}\)。

因此有 \(\# \text{ loops}=\#\text{ edges}-(\#\text{ nodes}-1)=\#\text{ edges}-\#\text{ nodes}+1\)。

移项得欧拉公式：

\[\begin{matrix} \#\text{ nodes} & -\#\text{ edges} & +\#\text{ loops} & =1\\ \end{matrix} \]

开头的图是针对多维立体图来讲的：

\[\begin{matrix} \#\text{ nodes} & -\#\text{ edges} & +\#\text{ loops} & =\dim-1\\ \end{matrix} \]

平面图就是 dim-1 = 2-1 = 1，立体图就是 dim-1 = 3-1 = 2。

Kirchhoff’s law

两个零空间之间可以用欧姆定律联系起来，这里的 C 是电导，当时用 G 表示，代表 1/R。

这里两个方程不再是齐次了，左面那个 e 比较好理解，就是电势差。右边得 f 代表外接电流源。

最终合体：\(\boldsymbol{A}^\mathrm{T}\boldsymbol{CAx}=\boldsymbol{f}\)。