1.11 The Four Fundamental Subspaces 阅读笔记
reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。
四个基本子空间
reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。
Reference
- Course website: The Four Fundamental Subspaces | Unit I: Ax = b and the Four Subspaces | Linear Algebra | Mathematics | MIT OpenCourseWare
- Course video: 【完整版-麻省理工-线性代数】全34讲 配套教材_哔哩哔哩_bilibili
- Course summary: Lecture 10: The four fundamental subspaces (mit.edu)
- Extra reading: Section 3.5 in Introduction to Linear Algebra, Fifth Edition by Gilbert Strang.
为什么 \((1,1,2)\)，\((2,2,5)\)，\((3,3,8)\) 也是线性相关的？
凑成方阵 \(\begin{bmatrix} 1 & 2 & 3\\ 1 & 2 & 3\\ 2 & 5 & 8 \end{bmatrix}\) 发现前两行是一样的，reduced echelon form 至少消去一行。所以行向量线性相关，列向量也线性相关。
列怎么样和行怎么样有一些关系，这个在今天的讨论范围内。
Four Fundamental Subspaces
对于一个矩阵 \(\boldsymbol{A}_{m\times n}\)，有如下四个基本子空间：
Column Space（列空间）：\(\boldsymbol{C}(\boldsymbol{A})\in\R^{m}\)
Null Space（零空间）：\(\boldsymbol{N}(\boldsymbol{A})\in\R^{n}\)
Row Space（行空间）：\(\boldsymbol{C}(\boldsymbol{A}^\mathrm{T})\in\R^{n}\)（行向量线性组合的空间，也就是A转置的列空间）
Left Null Space（左零空间）：\(\boldsymbol{N}(\boldsymbol{A}^\mathrm{T})\in\R^{m}\)（先不说为什么叫“左”零，是ATy=0的解空间）
Basis, Dimension, and Big Picture
这是 Unit 1 的 big picture。
- 为什么行空间和列空间的维度是一样的？
- 为什么左零空间的维度是 \(m-r\)？
- \(\dim \boldsymbol{C}(\boldsymbol{A}^\mathrm{T}) +\dim \boldsymbol{N}(\boldsymbol{A})=n\)，\(\dim \boldsymbol{C}(\boldsymbol{A}) +\dim \boldsymbol{N}(\boldsymbol{A}^\mathrm{T})=m\)，为什么是这么组合？
第三个问题可以回答，因为行空间和零空间都属于 \(\R^n\)，另外两个属于 \(\R^m\)，因此这么组合。行空间和零空间构成 \(\R^n\)，列空间和左零空间构成 \(\R^m\)。
Column Space
\(r\) 个主元构成的列形成了列空间的基，\(\dim \boldsymbol{C}(\boldsymbol{A})=r\)。
Null Space
\(n-r\) 个 special solutions 形成了零空间的基，\(\dim \boldsymbol{N}(\boldsymbol{A})=n-r\)
Row Space
通过 row operation 可以得到 Reduced Echelon Form。
\(\boldsymbol{A}= \begin{bmatrix} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \\ \end{bmatrix} \underrightarrow{\text{Reduced Echelon Form}} \begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}=\boldsymbol{R} \\\)
左边，\(\boldsymbol{C}(\boldsymbol{A})\) 可以表示出第三个分量非零的向量。但是右边，\(\boldsymbol{C}(\boldsymbol{R})\) 无论怎么表示第三个分量永远是零。因此有 \(\boldsymbol{C}(\boldsymbol{A})\ne\boldsymbol{C}(\boldsymbol{R})\)。
但是 row operation 本质上是对行向量的线性组合，左边的行向量经过线性组合能表示出右边的行向量，因此两边行向量线性组合出的空间是一样的，因此必然有：\(\boldsymbol{C}(\boldsymbol{A}^\mathrm{T})=\boldsymbol{C}(\boldsymbol{R}^\mathrm{T})\)。
而零向量必不可能在基里面，因为零向量和任何向量线性相关。而 \(r\) 个主元所在行也是线性无关的，因为行向量前 \(r\) 个元素是单位向量，非零的线性组合不可能把这些元素组成零。因此：
\(r\) 个 Reduced Echelon Form矩阵R的非零行构成行空间的基，\(\dim \boldsymbol{C}(\boldsymbol{A}^\mathrm{T})=r\)
列空间的维度等价于矩阵的秩，因此矩阵和矩阵转置的秩也是一样的。
Left Null Space
为什么叫做“左”零空间呢？因为有 \(\boldsymbol{A}^\mathrm{T}\boldsymbol{y}=\boldsymbol{0}\Rightarrow \boldsymbol{y}^\mathrm{T}\boldsymbol{A}=\boldsymbol{0}^\mathrm{T}\)。未知量在左边，零向量躺着，故叫做左零空间。
把 \(\boldsymbol{A}^\mathrm{T}\) 看作 \(\boldsymbol{A}'\)，大小为 \(n\times m\)。因此其零空间的维度为 \(m-r\)（转置的秩等于原来的秩）。
但是基是什么呢？再次观察 Reduced Echelon Form：
我们知道 \((\boldsymbol{P})\boldsymbol{E}\boldsymbol{A}=\boldsymbol{R}\)（讲义里面很仔细地解释了）
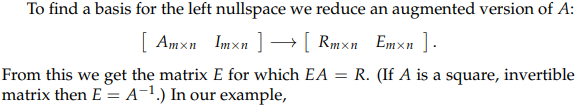
仍然用 Row Space 的例子：
\(\boldsymbol{E}\boldsymbol{A}= \boldsymbol{E}\cdot\begin{bmatrix} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \\ \end{bmatrix}=\begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}=\boldsymbol{R} \\\)
\(R\) 的最后一行全是零，这是因为 \(E\) 的最后一行同 \(A\) 的每一列相乘的结果都是 0。所以 \(E\) 最后一行的行向量乘以 \(A\) 得到行零向量，也就是说 \(E\) 的最后一行就是 \(\boldsymbol{y}^\mathrm{T}\)！\(E\) 代表着行变换，\(E\) 的最后一行正记录怎样对行向量线性组合凑出零行向量（最后一行）
对于任意的矩阵 \(A\)，\(R\) 最下面 \(m-r\) 行全是零，所以 \(E\) 最下面 \(m-r\) 行必然满足 \(\boldsymbol{y}^\mathrm{T}\boldsymbol{A}=\boldsymbol{0}^\mathrm{T}\)。而且必然是线性无关的。因为 \(E\) 是由单位矩阵 I 的单位向量线性组合出来的，其行向量一定还可以可逆地组合回去成为单位向量，因此这些行向量的表示能力等同于单位向量的表示能力，单位向量线性无关那么构成 \(E\) 的行向量也线性无关。因此：
得到Reduced Echelon Form的行变换矩阵E的后 \(m-r\) 行构成左零空间的基，\(\dim \boldsymbol{N}(\boldsymbol{A}^\mathrm{T})=m-r\)
New Vector Space
线性空间，向量空间的元素不一定是实数向量。也可以是所有 \(3\times 3\) 的矩阵！
只要满足线性空间的八条规律，对线性运算封闭，就可以将其当做线性空间中的元素。因为矩阵本身也满足线性空间的八条运算律，假设不算矩阵乘法，我们就可以将所有 \(3\times 3\) 的矩阵看做一个线性空间。它的子空间有上三角矩阵和对称矩阵。
子空间的交仍然是子空间，上三角矩阵和对称矩阵的交为对角矩阵，仍然为子空间。
其维度为3，一组基为：
研究角度从 \(\R^n\) 变成了 \(\R^{n\times n}\)。
