1.8 Solving Ax = 0: Pivot Variables, Special Solutions 阅读笔记

齐次线性方程求解，秩和主元

reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。

Reference

1. Course website: Solving Ax = 0: Pivot Variables, Special Solutions | Unit I: Ax = b and the Four Subspaces | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video: 【完整版-麻省理工-线性代数】全34讲+配套教材_哔哩哔哩_bilibili
3. Course summary: Lecture 7: Solving Ax = 0: pivot variables, special solutions (mit.edu)
4. Extra reading: Section 3.2 in Introduction to Linear Algebra, Fifth Edition by Gilbert Strang.
5. Extra videos (3Blue1Brown):
   1. Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra - YouTube

---

上一讲介绍了何为零空间/齐次线性方程的解，这一讲介绍如何求零空间，这玩意大部分人应该都会吧，懒得整理了。

下面求解\(\boldsymbol{Ax}=\boldsymbol{0}\)：

Echelon Form and Rank

因为应用行变换有\(\boldsymbol{EPAx}=\boldsymbol{EP0}=\boldsymbol{0}\)，所以等同于解\(\boldsymbol{Ux}=\boldsymbol{0}\)，这里的\(\boldsymbol{U}\)是上三角的。

不过\(\boldsymbol{U}\)不一定是方阵，上三角也不一定像之前求方阵的逆一样搞成一格一格的。现在，\(\boldsymbol{U}\)的第i行如果没变成全0，左数第一个非零的元素就是主元，如果全0，就没有主元。

这种矩阵被称为Echelon Form，大概是阶梯的意思。举例：

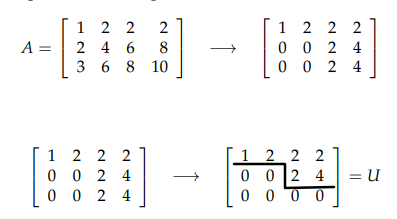
主元有两个，为\(\boldsymbol{A}_{11}\)和\(\boldsymbol{A}_{23}\)。定义秩 \(r\) 为主元的个数，秩的意义在于说明组成矩阵A的列向量只有多少个是独立的。

矩阵A的秩为2，说明矩阵A四个列向量张成的列空间只需要两个就能张成同样的列空间。\(\boldsymbol{A}_{22}=0\)，因为第二列和第一列共线。\(\boldsymbol{A}_{34}=0\)，因为第四列可以由第一列和第三列线性表示（-2倍第一列+2倍第三列=第四列）。所以第二列和第四列冗余了。

矩阵如果有 \(m\) 行 \(n\) 列，则秩 \(r\) 必满足 \(r\le{m}\text{ and }r\le{n}\)。

Special Solutions

化成\(\boldsymbol{Ux}=\boldsymbol{0}\)便可以使用回代求解。我们都知道可以对自由变量（非主元）赋任意值，然后把约束变量（主元）解出来。

矩阵 \(\boldsymbol{A}_{m\times n}\) 的秩为 \(r\)，那么就有 \(r\) 个约束变量，\(n-r\) 个自由变量。

如果每次对一个自由变量设为1，其他的自由变量全设为0，就会得到 \(n-r\) 个解，这些被称为特解。

为什么有 \(n-r\) 个自由变量呢？从方程的角度看很显然，但是不妨从线性空间的角度看。是因为有 \(n-r\) 个冗余的列向量，线性组合时，冗余的列向量的scale是可以任取的。

Reduced Row Echelon Form

这个就是大一解方程化成的标准型了，主元的那一列除了他自己其他元素全零，而且主元化为1。比如：

解得：

\[\begin{align*} \begin{cases} x_1=-2x_2+2x_4 \\ x_2=x_2+0x_4 \\ x_3=0x_2-2x_4 \\ x_4=0x_2+x_4 \end{cases} \Rightarrow \boldsymbol{x}&=x_2\begin{bmatrix} -2\\ 1\\ 0\\ 0 \end{bmatrix}+x_4\begin{bmatrix} 2\\ 0\\ -2\\ 1 \end{bmatrix}=\begin{bmatrix} -2 & 2\\ 1 & 0\\ 0 & -2\\ 0 & 1 \end{bmatrix}\begin{bmatrix} x_2\\ x_4 \end{bmatrix}\\&=\boldsymbol{N}\begin{bmatrix} x_2\\ x_4 \end{bmatrix} \end{align*} \]

矩阵\(\boldsymbol{N}\)为零空间矩阵，满足\(\boldsymbol{R}_{m\times{n}}\boldsymbol{N}_{n\times{n-r}}=\boldsymbol{O}\)，\(\boldsymbol{N}\)的列向量代表特解。

这种形式的好处是直接写出特解。非主元所在的列为自由变量，每一次让一个为1，其余为0，则约束变量就从非主元那一列从上往下写取相反数，写到全零行的0为止。

从矩阵角度：矩阵\(\boldsymbol{R}\)可以通过交换列向量变成如下形式：(F表示free columns)

\[\boldsymbol{R}=\begin{bmatrix} \boldsymbol{I}_{r\times{r}} & \boldsymbol{F}_{r\times{n-r}}\\ \boldsymbol{O}_{m\times{r}} & \boldsymbol{O}_{m\times{n-r}} \end{bmatrix},\boldsymbol{RN}=\boldsymbol{0}\Rightarrow \boldsymbol{N}=\begin{bmatrix} -\boldsymbol{F}\\ \boldsymbol{I}_{n-r\times{n-r}} \end{bmatrix} \]

实际的解还需要把列向量交换回去。

Structure of Solution

这里讨论一下解的结构。自由变量有 \(n-r\) 个，大于等于零。如果为零，那么没有自由变量，就不会有列向量冗余，所有列向量线性无关/独立，那么若想线性组合出零向量，系数必须全为0，也就是解唯一，且只为零向量。

如果大于0，就有列向量冗余就会有零空间矩阵N。