1.1 The Geometry of Linear Equations 阅读笔记

从线性代数的角度看线性方程组

reference的内容为唯一教程，接下来的内容仅为本人的课后感悟，对他人或无法起到任何指导作用。

Reference

1. Course website: The Geometry of Linear Equations | Unit I: Ax = b and the Four Subspaces | Linear Algebra | Mathematics | MIT OpenCourseWare
2. Course video (bilibili): 麻省理工 2011新版 线性代数 MIT 18.06SC Linear Algebra, Fall 2011（中英）_哔哩哔哩_bilibili
3. Course summary: The Geometry of Linear Equations (mit.edu)
4. Extra reading: Section 1.1 in Introduction to Linear Algebra, Fifth Edition by Gilbert Strang.
5. Extra videos (3Blue1Brown):
   1. Vectors | Chapter 1, Essence of linear algebra - YouTube
   2. Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra - YouTube

---

解方程组，是线性代数这个讲座里梦开始的地方：

\[\begin{cases} \begin{aligned} 2x & -y & =0 \\ -x & +2y & =3 \end{aligned} \end{cases} \]

接下来第一讲让我从三种角度来看待这个方程组。

Row Picture

row是行的意思，column是列的意思。从行的角度，意思就是把每一行的方程给联立起来，从几何角度上看，每一行方程相当于一条直线，多个直线求出它们的交点。对于三维，每一行变成了平面。三个平面才有可能出现一个交点。对于更高维就变成超平面的交点了。

很简单，没学线代之前我一直对方程组就是这样子理解的（大一学完之后也是这么理解的......）。

Column Picture

这个就比较有意思了，我竟然到大四才知道还可以这么想😅（或许大一我知道但是忘了）。把竖着看每一列的系数看作向量（Vector）：

\[x \begin{bmatrix} 2\\ -1 \end{bmatrix} +y \begin{bmatrix} -1\\ 2 \end{bmatrix}= \begin{bmatrix} 0\\ 3 \end{bmatrix} \]

什么是向量呢？课程视频里面没有仔细说，但是可以看看补充材料，就当作一个箭头吧（高中）。

于是方程组可以看成“数乘以向量的加和”等于一个“新的向量”，我们把“数乘以向量的加和”叫做向量之间的线性组合（Linear Combination）。

学完一轮线代的我：卧*原来方程组可以看成是向量之间的线性组合啊。

几何上的表示呢？相加就是首尾相接了，标乘就是拉伸了。直接copy人家的图：

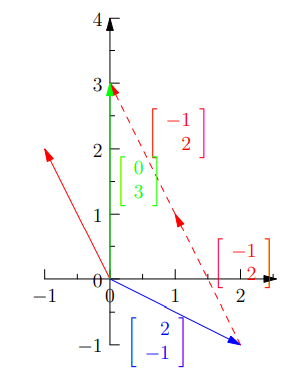
Linear Independence

对于上面的图，如果\(x\), \(y\)任取的话，那线性组合出来的向量会是什么样子呢？

在这个例子里面它可以是\(xy\)平面内任意的向量，但是其他情况呢？比如两个共线的向量线性组合还得在这个线上面蹦跶。三个共面的向量线性组合还得在这个面上蹦跶，不可能跑到平面外的空间。

讲座就说了，如果\(x\), \(y\) (,\(z\)) 任取的话，线性组合的2维/3维向量不能填满整个\(xy\)(\(z\))平面，那么用来线性组合的向量就是线性相关的（Linear Dependent）。

讲座最后还说了，在线性相关的情况下，会有向量是多余的。比如三个共面的向量能线性组合出来一个平面，那肯定用两个向量就能线性组合出来同样的平面。

讲座还说了，线性无关（Linear Independent）的n维向量们线性组合出来的向量集合是可以填满整个n维空间的。但是有个坑别掉进去了：讲座和summary可从来没说什么是线性无关的，反正\(x\), \(y\) 任取使得线性组合的2维向量能填满\(xy\)平面的一组向量不一定是线性无关的。毕竟假如我有10000个2维向量，只要有一个不共线，肯定能填满，但是这并不是线性无关的，因为有9998个多余的向量。

线性无关和线性相关之前学过，在这里悄悄地串起来了。其实还悄悄带入了一点基（basis）和生成子空间/张成空间（span）的概念。

Matrix Picture

\[\begin{align*} \begin{bmatrix} 2 & -1\\ -1 & 2 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} &= \begin{bmatrix} 0\\ 3 \end{bmatrix} \text{ 可以视作} \\ \mathbf{A} \mathbf{x} &=\mathbf{b} \end{align*} \]

从matrix的角度再看一遍线性相关：对于任意的\(\mathbf{b}\)，如果不存在\(\mathbf{x}\)使得等式成立，那么组成矩阵\(\mathbf{A}\)的向量是线性相关的，矩阵\(\mathbf{A}\)是奇异（singular）的。（始终鸡贼地避开了线性无关的概念）

Matrix Multiplication

column picture让我对矩阵乘法也有了新的看法了。我大可以继续按照原有的standard的方式来背矩阵乘法公式（i行和j列对应元素相乘相加得到i行j列的元素值）：

\[\begin{bmatrix} 2 & -1\\ -1 & 2 \end{bmatrix} \begin{bmatrix} 1\\ 2 \end{bmatrix} = \begin{bmatrix} 2\times1+(-1)\times2\\ (-1)\times1+2\times2 \end{bmatrix} = \begin{bmatrix} 0\\ 3 \end{bmatrix} \]

但是学完column picture就可以线性组合了啊，要是高中能这样子理解就一下子记住了啊：

\[\begin{bmatrix} 2 & -1\\ -1 & 2 \end{bmatrix} \begin{bmatrix} 1\\ 2 \end{bmatrix} = 1 \begin{bmatrix} 2\\ -1 \end{bmatrix} +2 \begin{bmatrix} -1\\ 2 \end{bmatrix} = \begin{bmatrix} 2\\ -1 \end{bmatrix} + \begin{bmatrix} -2\\ 4 \end{bmatrix} = \begin{bmatrix} 0\\ 3 \end{bmatrix} \]

然后这个讲座就结束了，可是我补充看了一点Vector和Linear Combination的内容，也觉得蛮有意思的。

Vector

不同人看待向量用不同的方式，实际生活中有各种物理量因为有方向，就看做向量，是一个有大小和方向的箭头，因此被不少人叫做矢量。而这个讲座里面的向量均是用数字表示的。换言之，一个是可视化形式，一个是数据形式。

数据形式的向量通常写成上面竖着一列的样子：\(\begin{bmatrix} v_1 \\ \vdots \\ v_n \end{bmatrix}\)。但是这样太占空间了，因此这个教材会写成\((v_1, \cdots, v_n)\)来表示。但是仍然代表一个column而不是row。（书上认为中括号和小括号的意义是不一样的，而我第一次学的教材是等同的，因为碰到这个问题都会横着写再加一个矩阵转置符号）

然后说了向量的两种最基本的运算：加法和标乘，期间还提到了零向量。这些概念的数据形式和可视化形式就不展开了。

线性组合就是向量加法和标乘的结合了。

其实数字和可视化是不分家的。解决物理问题的时候不可避免要用计算机建模，那么所有箭头一样的物理量统统会转成数字。而做数据分析的时候，又会把一个个数据化的向量转换成可视化的箭头或者点，去分析pattern。

只不过数学家们还有第三种视角，就是纯抽象的形式了。只有一个表示向量的符号\(\mathbf{v}\)和一些运算符\(+\)和\(×\)。

Linear Combination, Span, and Basis

下意识就会对一个比如坐标\((1,2)\)的向量\(\mathbf{v}\)画一个平面直角坐标系，然后标上点横坐标1，纵坐标2，从原点画一个有向箭头指向这个点。

但是这建立的条件是我们以平面直角坐标系的单位向量\(\mathbf{i}=(1,0)\)和\(\mathbf{j}=(0,1)\)作为基。因为\(\mathbf{v}=1\mathbf{i}+2\mathbf{j}\)，所以坐标为\((1,2)\)。如果采用新的基\(\mathbf{a}\)和\(\mathbf{b}\)得到\(\mathbf{v}=c\mathbf{a}+d\mathbf{b}\)，那坐标就变成\((c,d)\)了。

显然，这说明一个向量可以由不同的向量用不同的方式线性组合，那么为什么线性组合叫做线性呢？3Blue1Brown说，只控制线性组合的一个标量改变，其余固定，表示出来的向量的“箭头部分的点的轨迹”为直线，他认为这体现了“线性”，我觉得蛮有道理的。

接着就提出了span的概念，也就是张成空间/线性子空间。说线性组合的向量构成的集合就被称为一个span。也就是说span是向量的集合。那么为什么向量的集合会用“空间”这个术语呢？因为某种程度上，线代里面的向量起始点都在原点，那么只要关注箭头部分的点是谁就可以了，向量就被看做了一个点（我猜用括号形式表示向量的一个原因就是这个吧，因为点的坐标也是括号表示的）。那么span就变成了“箭头部分的点的轨迹”，就变成一个空间了。

接着开始从1维的1个向量的span到3维的3个向量的span分析。1维的span要么是线，要么是点（0向量）。2维的span可以是平面（flat sheet）。但是如果两个向量共线，那必然只能表示一个线了，比如说两个实数相加的结果一定待在实轴上，是不可能有虚数的。再看，两个向量共线时，其中一个向量绝对可以由另一个向量线性组合得到（就是标乘了），那么其实两个向量的span能力和一个是一样的了，都是线，有向量浪费了。3维也是这个道理，如果三个向量中两个向量可以span第三个，那这第三个向量根本就不需要，剩下的向量张成的空间和三个向量张成的空间是一样的。

如果一组向量中不存在哪个向量可以由其他的向量线性表示，那么这组向量是线性无关的，也就是说不存在多余的向量。

而基就是一组可以张成n维空间的n维线性无关向量。首先他没有多余的向量，然后他能表示出一个full vector space。比如\((1,0,\cdots省略一万个0)\)和\((0,1,\cdots省略一万个0)\)虽然线性无关，但是只能表示一个flat sheet，而不是10002维的空间，因此不是基。