论文阅读笔记：A Syntactic Neural Model for General-Purpose Code Generation

目前看的一些Text2SQL论文用seq2seq模型。decoder端一般用现成的这个模型A Syntactic Neural Model for General-Purpose Code Generation，将encoder得到的embeddings送入这个decoder获得AST再获得SQL语句。于是大概了解了一下原理，跳过结论分析部分。

（正文为工地英语）

Abstract

  • Consider underlying syntax.
  • Powered by a grammar model.
  • Use AST grammar to restrain decoder.

Introduction

  • Structural data-based code generation: NL -> AST <-> structural code
    • Reduce search space: use a sequential action (apply production rules, emit terminal tokens) as AST.
    • Model information flows (parents+left siblings->current node) with NN.

The Code Generation Problem

image-20220110230548377

image-20220110230335230

  • Objective:

    • Get the best possible AST \(\hat{y}\) from input NL \(x\).

      \[\hat{y}=\mathop{\arg\max}\limits_{y}{p(y|x)} \]

    • Generate oracle AST \(y\) from code \(c\) deterministically.

    • Compute loss and optimize.

  • AST:

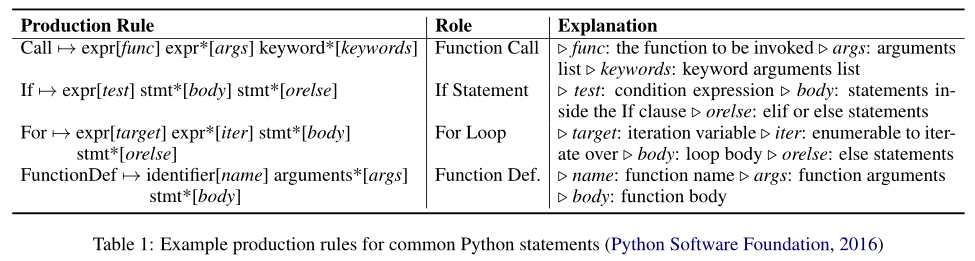
    • AST is composed of production rules.
    • Production rules are composed of a head node and several child nodes.
    • Nodes are classified as terminal (operation, variable) and non-terminal.

Grammar Model

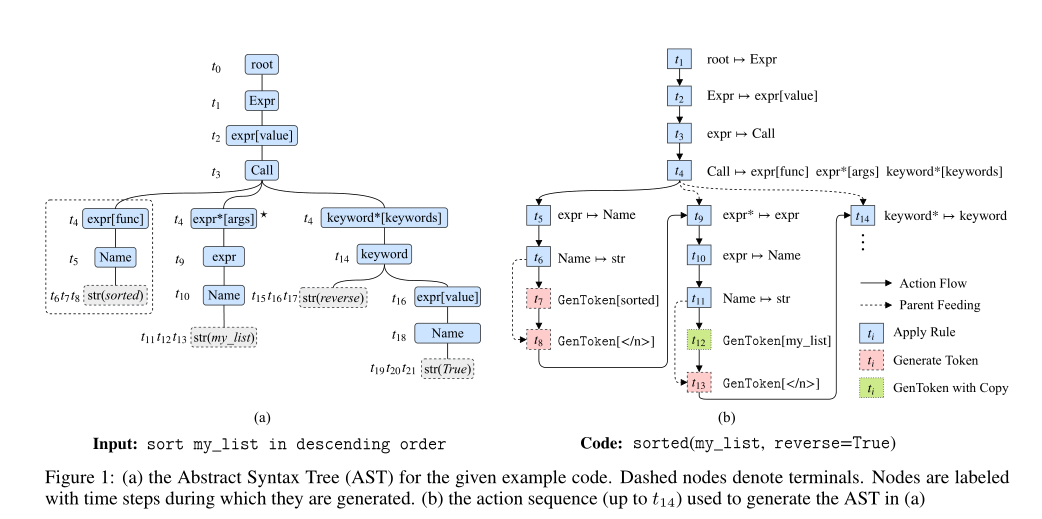
  • Two actions:

    • \(\text{ApplyRule}[r]\): apply production rules.
      • Generate program structure.
      • Expand current node in DFS and left2right order.
      • Current visiting node at time \(t\) is called frontier node \(n_{f_t}\).
      • When a terminal node is added, switch to \(\text{GenToken}[v]\).
      • Unary closure: merge many production rules in a single rule. reduce the number of actions but increase the size of grammar.
    • \(\text{GenToken}[v]\): Generate terminal tokens.
      • We have more than one tokens: "hello world" has 2 tokens.
      • Do \(\text{GenToken}[v]\) in multiple steps with </n> to close.
        • \(\text{GenToken}[\text{"hello world"}]:=\text{GenToken}[\text{"hello"}]\text{GenToken}[\text{"world"}]\text{GenToken}[\text{"<\\n>"}]\)
      • Pre-defined or copy from users' input.

  • Calculate \(p(y|x)\)

    • \[p(y|x)=\prod_{t=0}^{T}p(a_t|x,a_{<t}) \]

      where \(a_t\) is the action of time \(t\) in the AST and \(a_{<t}\) is the sequence of actions \(a_0a_1a_2...a_{t-1}\).

Estimating Action Probabilities

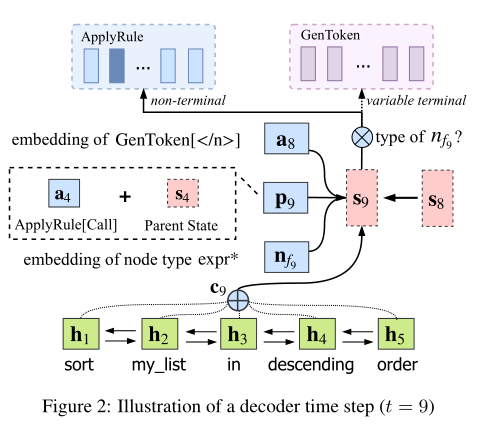
image-20220110230247922

  1. Encode hidden embedding \(\mathbf{h}_i^{(t)}\) for each time step \(t\) from \(1\) to \(T\), NL \(x^{(t)}\) is composed of \(\{w_i^{(t)}\}_{i=1}^{n}\).

    \[\mathbf{h}_i^{(t)}=\mathbf{f}_{BiLSTM}(\{w_i^{(t)}\}_{i=1}^{n}, w_i^{(t)}) \]

  2. \(\mathbf{a}_t\) is the embedding of action \(a_t\), classified as \(\text{ApplyRule}[r]\) and \(\text{GenToken}[v]\). \(\mathbf{W_R}\) and \(\mathbf{W_G}\) are the embedding matrices whose row denotes action embedding \(\mathbf{a}\).

    \[\mathbf{a}_t=\begin{cases} \mathbf{W}_R\cdot\mathbf{e}(r_t) & \text{ if } a_t= \text{ApplyRule}[r_t] \\ \mathbf{W}_G\cdot\mathbf{e}(v_t) & \text{ if } a_t= \text{GenToken}[v_t] \end{cases} \]

    where \(\mathbf{e}(\cdot)\) represents one-hot vectors.

  3. \(\mathbf{c}_t\) is the context embedding of \(\{\mathbf{h}_i^{(t)}\}_{i=1}^n\) via soft attention.

    \[\mathbf{c}_t=\sum_{i=1}^{n}\omega (\mathbf{h}_i^{(t)})\mathbf{h}_i^{(t)} \]

    where \(\omega(\cdot)\) is a DNN with a single hidden layer.

  4. \(\mathbf{p}_t\) is the parent embedding of current frontier node \(n_{f_t}\).

    \(p_t\) is the time step when \(n_{f_t}\) is formed, called parent action step. (e.g. \(p_9=t_4\), \(p_8=t_6\))

    \[\mathbf{p}_t=[\mathbf{a}_t:\mathbf{s}_t] \]

    where \([:]\) denotes concatenate and \(\mathbf{s}_t\) denotes the internal hidden state in \(f_{LSTM}(\cdot)\) (will be mentioned below).

  5. \(\mathbf{n}_{f_t}\) is the node type embedding of \(n_{f_t}\). I guess it is calculated in this way..?

    \[\mathbf{n}_{f_t}=\mathbf{W}_N\cdot\mathbf{e}(n_{f_t}) \]

  6. Update internal hidden state \(\mathbf{s}_t\) with vanilla LSTM.

    \[\mathbf{s}_t=\mathbf{f}_{LSTM}([\mathbf{a}_{t-1}:\mathbf{c}_t:\mathbf{p}_t:\mathbf{n}_{f_t}],\mathbf{s}_{t-1}) \]

  7. Compute \(p(a_t|x,a_{<t})\):

    \[p(a_t|x,a_{<t})=\begin{cases} p(a_t=\text{ApplyRule}[r]|x,a_{<t}) & \text{ if } n_{f_t} \text{ is non-terminal} \\ p(a_t=\text{GenToken}[v]|x,a_{<t}) & \text{ if } n_{f_t} \text{ is terminal} \end{cases} \]

    1. \(p(a_t=\text{ApplyRule}[r]|x,a_{<t})\):

      \[p(a_t=\text{ApplyRule}[r]|x,a_{<t})=\mathbf{f}_{softmax}(\mathbf{W}_R\cdot \mathbf{g}(\mathbf{s}_t))\mathsf{T}\cdot \mathbf{e}(r) \]

      where \(\mathbf{g}(\cdot)=tanh(\cdot)+\mathbf{b}\).

    2. \(p(a_t=\text{GenToken}[v]|x,a_{<t})\):

      \[\begin{equation*} \begin{aligned} p(a_t=\text{GenToken}[v]|x,a_{<t})&=p(gen|x,a_{<t})p(v|gen,x,a_{<t})\\ &+p(copy|x,a_{<t})p(v|copy,x,a_{<t}) \end{aligned} \end{equation*} \]

      where \(gen\) denotes using pre-defined vocabulary and \(copy\) denotes copying users' input.

      \[\begin{bmatrix} p(gen|x,a_{<t}) \\ p(copy|x,a_{<t}) \end{bmatrix} =\mathbf{f}_{softmax}(\mathbf{W}_s\cdot\mathbf{s}_t) \]

      I guess \(\mathbf{W}_s \in \mathbb{R}^{2\times D_{\mathbf{s}_t}}\)?

      \[p(v|gen,x,a_{<t})=\mathbf{f}_{softmax}(\mathbf{W}_G\cdot \mathbf{g}([\mathbf{s}_t:\mathbf{c}_t])\mathsf{T}\cdot \mathbf{e}(v) \\ p(v|copy,x,a_{<t})=\frac{\exp{(\omega{(v,\mathbf{s}_t,\mathbf{c}_t)})}}{\sum_{i=1}^{n}\exp{(\omega{(h_i^{(t)},\mathbf{s}_t,\mathbf{c}_t)})}} \]

      where \(\omega(\cdot)\) is a DNN with a single hidden layer.

  8. Get the best possible AST \(\hat{y}\) from input NL \(x\).

    \[\hat{y}=\mathop{\arg\max}\limits_{y}{p(y|x)} \]

  9. Maximize the log-likelihood with oracle AST \(y\) from code \(c\).

  10. At inference time, use beam search to approximate \(\hat{y}\).

Experimental Evaluation

  • Metrics: accuracy and BLEU-4.
  • Error analysis:
    • Using different parameter names / omitting default values are rare.
    • Partial implementation (most).
    • Malform English inputs.
    • Pre-processing errors.
    • Other reason hard to categorize.
posted @ 2022-01-10 23:30  WIND_LIKE  阅读(420)  评论(0)  编辑  收藏  举报
Live2D