Tensorflow2.0笔记38——ResNet
Tensorflow2.0笔记
本博客为Tensorflow2.0学习笔记,感谢北京大学微电子学院曹建老师
4.5 ResNet
import tensorflow as tf
import os
import numpy as np
from matplotlib import pyplot as plt
from tensorflow.keras.layers import Conv2D, BatchNormalization, Activation, MaxPool2D, Dropout, Flatten, Dense
from tensorflow.keras import Model
np.set_printoptions(threshold=np.inf)
cifar10 = tf.keras.datasets.cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
class ResnetBlock(Model):
def __init__(self, filters, strides=1, residual_path=False):
super(ResnetBlock, self).__init__()
self.filters = filters
self.strides = strides
self.residual_path = residual_path
self.c1 = Conv2D(filters, (3, 3), strides=strides, padding='same', use_bias=False)
self.b1 = BatchNormalization()
self.a1 = Activation('relu')
self.c2 = Conv2D(filters, (3, 3), strides=1, padding='same', use_bias=False)
self.b2 = BatchNormalization()
# residual_path为True时,对输入进行下采样,即用1x1的卷积核做卷积操作,保证x能和F(x)维度相同,顺利相加
if residual_path:
self.down_c1 = Conv2D(filters, (1, 1), strides=strides, padding='same', use_bias=False)
self.down_b1 = BatchNormalization()
self.a2 = Activation('relu')
def call(self, inputs):
residual = inputs # residual等于输入值本身,即residual=x
# 将输入通过卷积、BN层、激活层,计算F(x)
x = self.c1(inputs)
x = self.b1(x)
x = self.a1(x)
x = self.c2(x)
y = self.b2(x)
if self.residual_path:
residual = self.down_c1(inputs)
residual = self.down_b1(residual)
out = self.a2(y + residual) # 最后输出的是两部分的和,即F(x)+x或F(x)+Wx,再过激活函数
return out
class ResNet18(Model):
def __init__(self, block_list, initial_filters=64): # block_list表示每个block有几个卷积层
super(ResNet18, self).__init__()
self.num_blocks = len(block_list) # 共有几个block
self.block_list = block_list
self.out_filters = initial_filters
self.c1 = Conv2D(self.out_filters, (3, 3), strides=1, padding='same', use_bias=False)
self.b1 = BatchNormalization()
self.a1 = Activation('relu')
self.blocks = tf.keras.models.Sequential()
# 构建ResNet网络结构
for block_id in range(len(block_list)): # 第几个resnet block
for layer_id in range(block_list[block_id]): # 第几个卷积层
if block_id != 0 and layer_id == 0: # 对除第一个block以外的每个block的输入进行下采样
block = ResnetBlock(self.out_filters, strides=2, residual_path=True)
else:
block = ResnetBlock(self.out_filters, residual_path=False)
self.blocks.add(block) # 将构建好的block加入resnet
self.out_filters *= 2 # 下一个block的卷积核数是上一个block的2倍
self.p1 = tf.keras.layers.GlobalAveragePooling2D()
self.f1 = tf.keras.layers.Dense(10, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())
def call(self, inputs):
x = self.c1(inputs)
x = self.b1(x)
x = self.a1(x)
x = self.blocks(x)
x = self.p1(x)
y = self.f1(x)
return y
model = ResNet18([2, 2, 2, 2])
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
checkpoint_save_path = "./checkpoint/ResNet18.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True)
history = model.fit(x_train, y_train, batch_size=32, epochs=5, validation_data=(x_test, y_test), validation_freq=1,
callbacks=[cp_callback])
model.summary()
# print(model.trainable_variables)
file = open('./weights.txt', 'w')
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
############################################### show ###############################################
# 显示训练集和验证集的acc和loss曲线
acc = history.history['sparse_categorical_accuracy']
val_acc = history.history['val_sparse_categorical_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
借鉴点:层间残差跳连,引入前方信息,减少梯度消失,使神经网络层数变身成为可能。
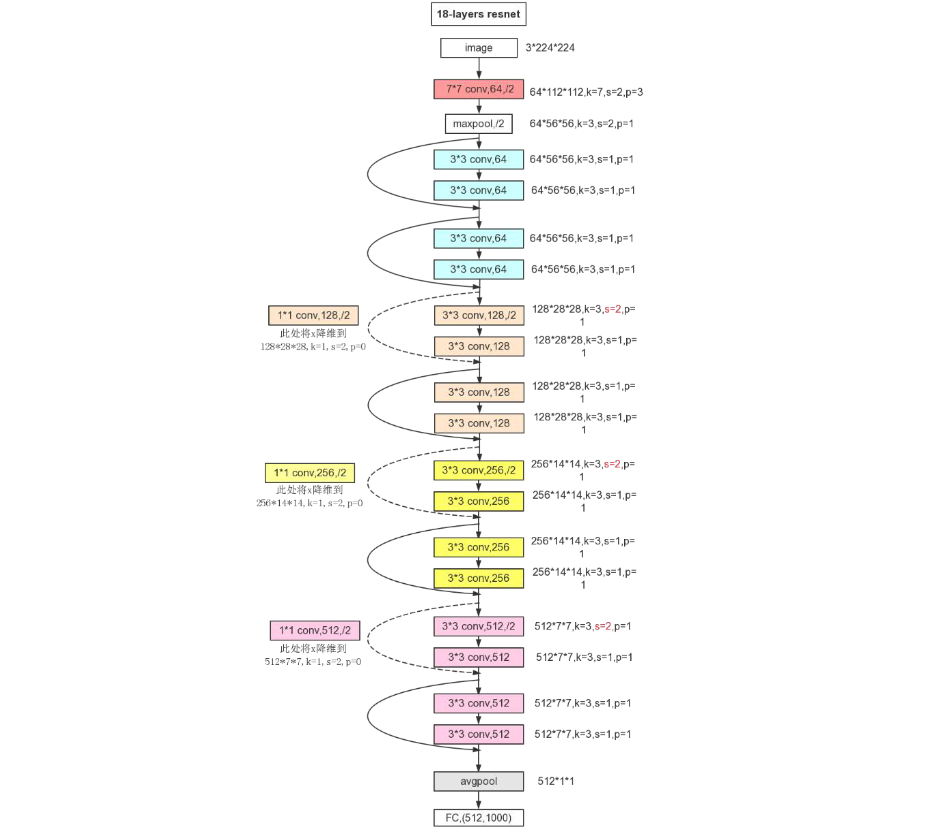
ResNet即深度残差网络,由何恺明及其团队提出,是深度学习领域又一具有开创性的工作,通过对残差结构的运用,ResNet使得训练数百层的网络成为了可能,从而具有非常强大的表征能力,其网络结构如下图所示。
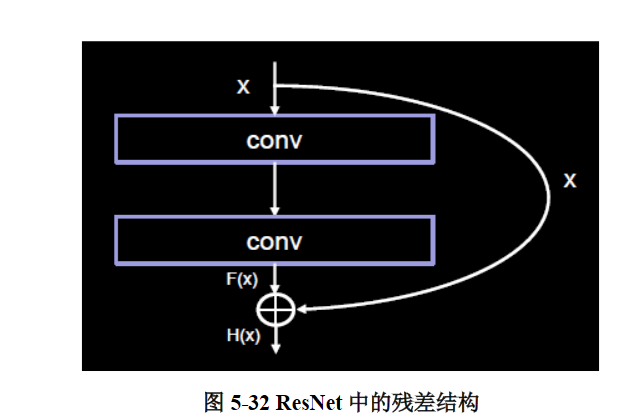
ResNet的核心是残差结构,如图5- 32所示。在残差结构中,ResNet不再让下一层直接拟合我们想得到的底层映射,而是令其对一种残差映射进行拟合。若期望得到的底层映射为H(x), 我们令堆叠的非线性层拟合另一个映射F(x) := H(x) – x,则原有映射变为F(x) + x。对这种新的残差映射进行优化时,要比优化原有的非相关映射更为容易。不妨考虑极限情况,如果一个恒等映射是最优的,那么将残差向零逼近显然会比利用大量非线性层直接进行拟合更容易。
值得一提的是,这里的相加与InceptionNet中的相加是有本质区别的,Inception中的相加是沿深度方向叠加,像“千层蛋糕”一样,对层数进行叠加;ResNet中的相加则是特征图对应元素的数值相加,类似于python语法中基本的矩阵相加。
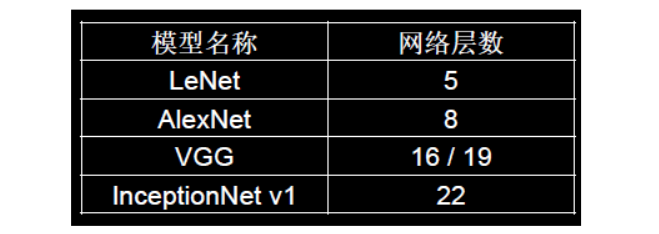
ResNet引入残差结构最主要的目的是解决网络层数不断加深时导致的梯度消失问题,从之前介绍的4种CNN经典网络结构我们也可以看出,网络层数的发展趋势是不断加深的。这是由于深度网络本身集成了低层/中层/高层特征和分类器,以多层首尾相连的方式存在,所以可以通过增加堆叠的层数(深度)来丰富特征的层次,以取得更好的效果。
但如果只是简单地堆叠更多层数,就会导致梯度消失(爆炸)问题,它从根源上导致了函数无法收敛。然而,通过标准初始化(normalized initialization)以及中间标准化层(intermediate normalization layer),已经可以较好地解决这个问题了,这使得深度为数十层的网络在反向传播过程中,可以通过随机梯度下降(SGD)的方式开始收敛。
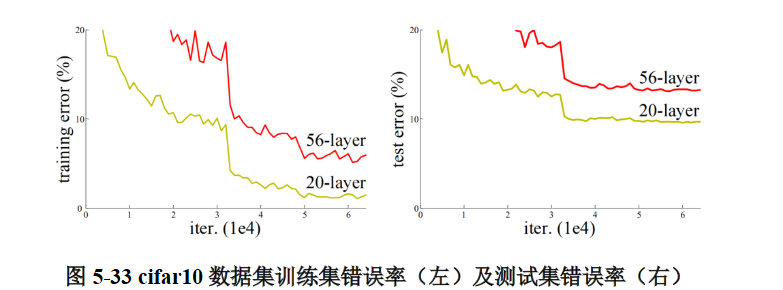
但是,当深度更深的网络也可以开始收敛时,网络退化的问题就显露了出来:随着网络深度的增加,准确率先是达到瓶颈(这是很常见的),然后便开始迅速下降。需要注意的是,这种退化并不是由过拟合引起的。对于一个深度比较合适的网络来说,继续增加层数反而会导致训练错误率的提升,图5- 33就是一个例子。
ResNet解决的正是这个问题,其核心思路为:对一个准确率达到饱和的浅层网络,在它后面加几个恒等映射层(即y = x,输出等于输入),增加网络深度的同时不增加误差。这使得神经网络的层数可以超越之前的约束,提高准确率。图5- 34展示了ResNet中残差结构的具体用法。
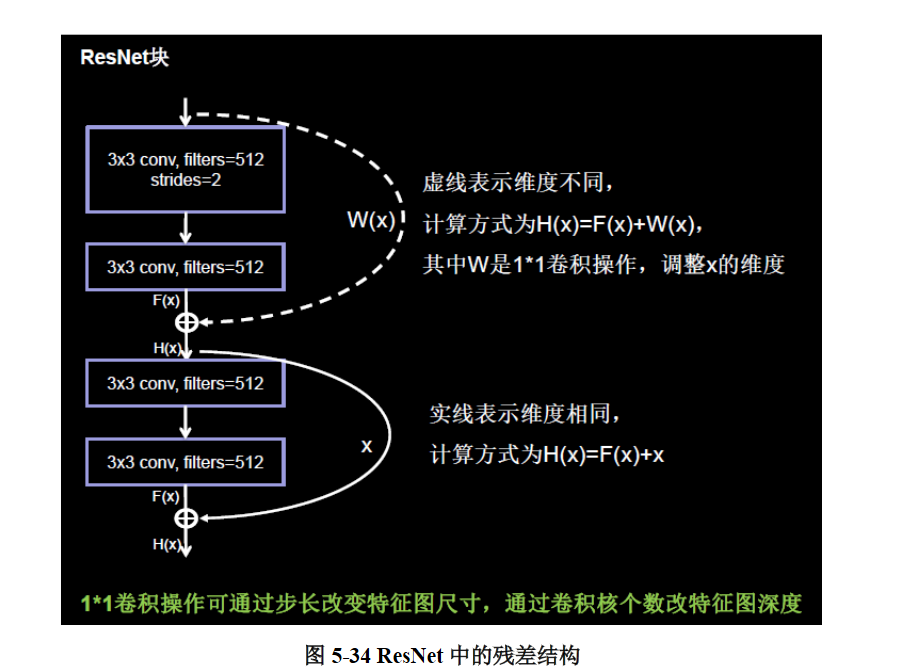
上图中的实线和虚线均表示恒等映射,实线表示通道相同,计算方式为H(x) = F(x) + x;虚线表示通道不同,计算方式为H(x) = F(x) + Wx,其中W为卷积操作,目的是调整x的维度(通道数)。我们同样可以借助tf.keras来实现这种残差结构,定义一个新的ResnetBlock类。
class ResnetBlock(Model):
def __init__(self, filters, strides=1, residual_path=False):
super(ResnetBlock, self).__init__()
self.filters = filters
self.strides = strides
self.residual_path = residual_path
self.c1 = Conv2D(filters, (3, 3), strides=strides, padding='same', use_bias=False)
self.b1 = BatchNormalization()
self.a1 = Activation('relu')
self.c2 = Conv2D(filters, (3, 3), strides=1, padding='same', use_bias=False)
self.b2 = BatchNormalization()
# residual_path为True时,对输入进行下采样,即用1x1的卷积核做卷积操作,保证x能和F(x)维度相同,顺利相加
if residual_path:
self.down_c1 = Conv2D(filters, (1, 1), strides=strides, padding='same', use_bias=False)
self.down_b1 = BatchNormalization()
self.a2 = Activation('relu')
def call(self, inputs):
residual = inputs # residual等于输入值本身,即residual=x
# 将输入通过卷积、BN层、激活层,计算F(x)
x = self.c1(inputs)
x = self.b1(x)
x = self.a1(x)
x = self.c2(x)
y = self.b2(x)
if self.residual_path:
residual = self.down_c1(inputs)
residual = self.down_b1(residual)
out = self.a2(y + residual) # 最后输出的是两部分的和,即F(x)+x或F(x)+Wx,再过激活函数
return out
卷积操作仍然采用典型的C、B、A结构,激活采用Relu函数;为了保证F(x)和x可以顺利相加,二者的维度必须相同,这里利用的是1 * 1卷积来实现(1 * 1卷积改变输出维度的作用在InceptionNet中有具体介绍)。利用这种结构,就可以利用tf.keras来构建出ResNet模型,如图5- 35所示
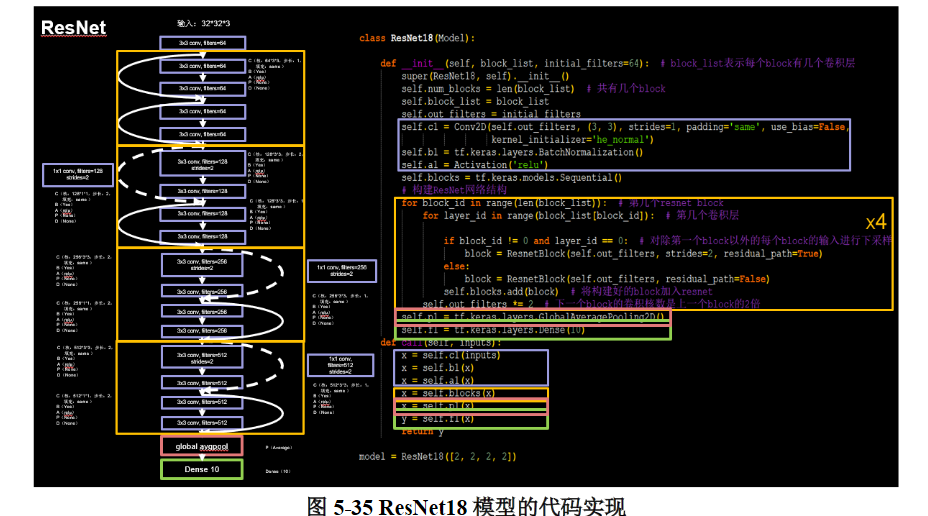
参数block_list表示ResNet中block的数量 ;initial_filters表示初始的卷积核数量。可以看到该模型同样使用了全局平均池化的方式来替代全连接层(关于全局平均池化的作用InceptionNet中有介绍)。
对于ResNet的残差单元来说,除了这里采用的两层结构外,还有一种三层结构,如图5- 36所示。
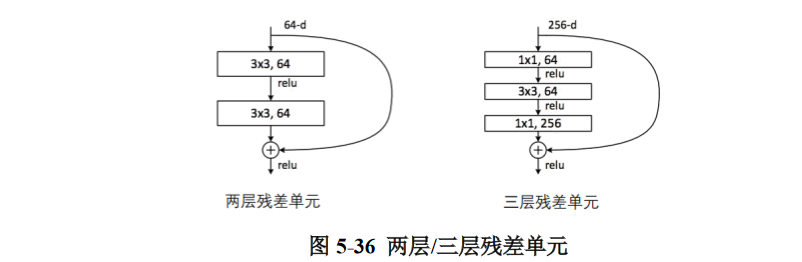
两层残差单元多用于层数较少的网络,三层残差单元多用于层数较多的网络,以减少计算的参数量。
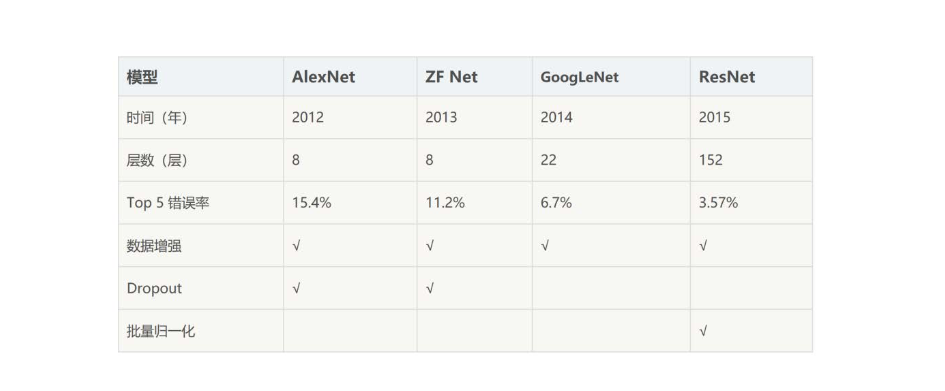
总体上看,ResNet取得的成果还是相当巨大的,它将网络深度提升到了152层 ,于2015年将ImageNet图像识别Top5错误率降至3.57 %。
4.6总结
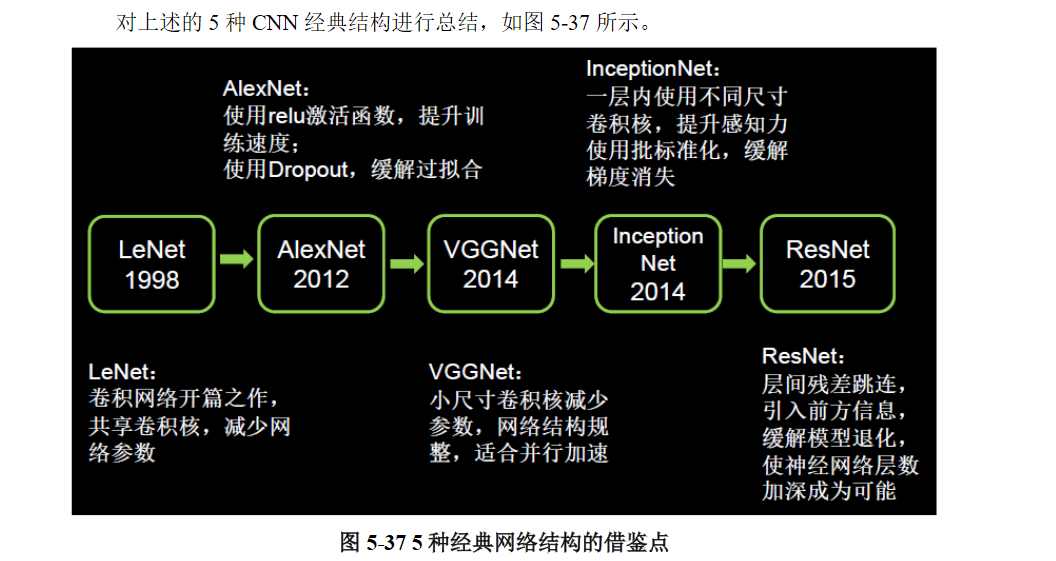
可以看到,随着网络复杂程度的提高,以及Relu、Dropout、BN等操作的使用,利用各个网络训练cifar10数据集的准确率基本上是逐步上升的。五个网络当中,InceptionNet的训练效果是最不理想的,首先其本身的设计理念是采用不同尺寸的卷积核,提供不同的感受野,但cifar10只是一个单一的分类任务,二者的契合度并不高,另外,由于本身结构的原因,InceptionNet的参数量和计算量都比较大,训练需要耗费的资源比较多,所以课堂上仅仅搭建了一个深度为10的精简版本(完整的InceptionNet v1,即GoogLeNet有22层,训练难度很大),主要目的是诠释InceptionNet的思路,并非单单追求cifar10数据集的准确率。
另外,需要指出的是,在利用这些网络训练cifar10数据集时,课程给出的源码并未包含其它的一些训练技巧,例如数据增强(对训练集图像进行旋转、偏移、翻转等多种操作,目的是增强训练集的随机性)、学习率策略(一般的策略是在训练过程中逐步减小学习率)、Batch size的大小设置(每个batch包含训练集图片的数量)、模型参数初始化的方式等等。然而实际上,一些训练方法和超参数的设定对模型训练结果的影响是相当显著的,以ResNet18为例,如果采取合适的训练技巧,cifar10的识别准确率是足以突破90 %的。所以,在神经网络的训练中,除了选择合适的模型以外,如何更好地训练一个模型也是一个非常值得探究的问题。



