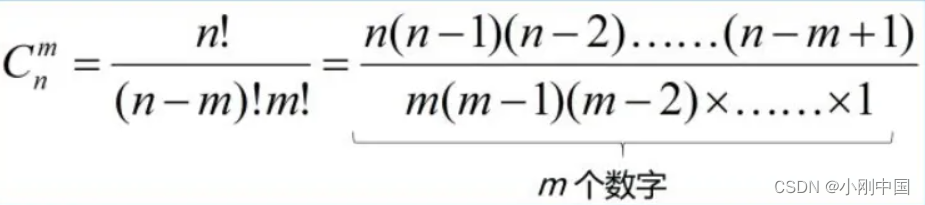关于动态规划算法
不去关注一些所谓算法，其实不知道其中味道如何，闲来无事：
最近看了下动态规划算法（LeetCodez中级题目），感觉蛮有意思的
先看下要求：
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？
eg:
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
eg: 输入：m = 7, n = 3 输出：28
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/unique-paths
其实最容易想到的：（一般是多少种可能，就是排列组合问题）
每次走完都要走 m+n-2 步骤，根据一层层深度，实际上这个是离散数据的问题
相当于 C(m+n-2, min(m-1,n-1))
不知道离散数学（这个是基础），这样就很简单了。
验证下：
3 7，那么n=8，m=2，即 8*7/(2*1) = 28
3 2 那么n=3，m=1，即3/1 = 3
3 3 那么n=4，m=2，即 4*3/(2*1) = 6
但这个存在一个问题，当n，m比较大的时候，计算会有溢出的风险。
例如： 10 10
此时n=18，m=9，相当于18*17........10 这个数字非常大
那么，有没有更方便的方法？
路线规划问题，直接分析代码（反正刚开始我也是没有想到这样的代码）
//////看注释即可
int uniquePaths(int m, int n) {
vector<vector<int>> f(m, vector<int>(n)); ///< 二维数组
//////////
for (int i = 0; i < m; ++i) {
f[i][0] = 1; ///< 第一行全为1，只有一种可能，从左边过来
}
for (int j = 0; j < n; ++j) {
f[0][j] = 1; ///< 第一列为1，只有一种可能，从上边过来
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
f[i][j] = f[i - 1][j] + f[i][j - 1]; ///< 从1，1开始计算，经过改点有多少种方法。即：左边有多少方法，上面过来有多少种方法，那么该点就两个方向相加的方法。
/////这里的概念一定要清晰，到达某个点的道路，是左边条数+上面条数
//eg：（1，1）=2；
//（2，3）=3；
//（3，3）=6；///< =(2,3)+(3,2)
}
}
return f[m - 1][n - 1];
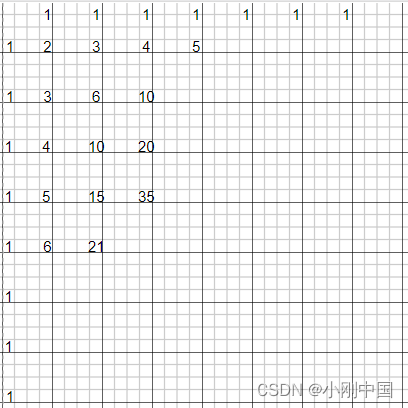
}大概如图，这么个意思：
这个莫非是杨辉三角？是的，就是著名的杨辉三角
当然，正常不会有这么简单算法。
例如，某个点是障碍点，且该点是不允许经过的，那么，代码要改下，原理类似：
到达某个点的道路，是左边条数+上面条数
【难度加大：⭐⭐⭐⭐】
其他条件不变，增加障碍物：
现在考虑网格中有障碍物。
网格中的障碍物和空位置分别用
1和0来表示
分析：
1.如果该点是障碍物，那么不管其前序到达多少，此时该点为0
2. 如果障碍物出现在第一行或第一列，那么改点以及后续点都到达数量为0
//////嗯，这里要考虑特殊情况，就是当第一个点就是障碍物时，此时直接返回0
show code
int uniquePathsWithObstacles(vector<vector<int>>& f) {
int m = f.size();
int n = f[0].size();
///特殊情况，第一个点就是障碍物，此时为0
if(f[0][0] == 1) {
return 0;
}
//////////
for (int i = 0; i < m; ++i) {
if(f[i][0] == 1) {
///当该点出现障碍物，那么意味着，后续点都是不可到达的
for(int k = i;k < m;++k) {
f[k][0] = 0;
}
i = m;
break;
} else {
f[i][0] = 1; ///< 第一行全为1，只有一种可能，从左边过来
}
}
///跳过第一点（这里跟上面不一致，实际上0,0 已经处理过）
for (int j = 1; j < n; ++j) {
if(f[0][j] == 1) {
///当该点出现障碍物，那么意味着，后续点都是不可到达的
for(int k = j;k < n;++k) {
f[0][k] = 0;
}
j = n;
break;
} else {
f[0][j] = 1;
}
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
if(f[i][j] == 1) {
f[i][j] = 0; ///< 该点是障碍物时，直接=0
} else {
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
}
}
return f[m - 1][n - 1];
}
如下图所示，这样应该比较直观点吧
离扫地机器人爬取路径又近了一步
