毒瘤的FFT笔记

自从机房掀起学习数学之风，我便跟风学起了数学（其实是因为不会）

众所周知FFT很有用（一开始真是不太好理解）。

首先上大佬的博客：

1.胡小兔（对不起我不如小学生）

2.路人黑的纸巾

3.GGN_2015

4.自为风月马前卒

接下来是正文（我抄的）。

FFT（Fast Fourier Transformation），中文名快速傅里叶变换，用来加速多项式乘法

前置知识：无吧？（反正我上数学课顺便看了看复数的基础知识就过来学了）

啊好吧还是有的

向量

同时具有大小和方向的量

在几何中通常用带有箭头的线段表示

圆的弧度制

等于半径长的圆弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度。用弧度作单位来度量角的制度叫做弧度制

公式:

1∘=π180rad1∘=π180rad

180∘=πrad180∘=πrad

平行四边形定则

 

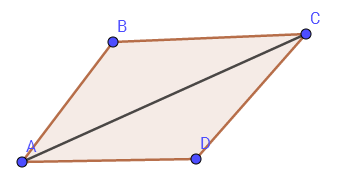
平行四边形定则：AB+AD=AC

系数表示法

设A(x)表示一个n−1次多项式

则A(x)=∑ni=0ai∗xi

例如：A(3)=2+3∗x+x2

利用这种方法计算多项式乘法复杂度为O(n2)

（第一个多项式中每个系数都需要与第二个多项式的每个系数相乘）

点值表示法

将nn互不相同的xx带入多项式，会得到nn个不同的取值yy

则该多项式被这nn个点(x1,y1),(x2,y2),…,(xn,yn))唯一确定

其中yi=∑n−1j=0aj∗xji

例如：上面的例子用点值表示法可以为(0,2),(1,6),(2,12)

利用这种方法计算多项式乘法的时间复杂度仍然为O(n^2)

（选点O(n)，每次计算O(n)）

复数

定义

设a,ba,b为实数，i2=−1i2=−1，形如a+bia+bi的数叫复数，其中ii被称为虚数单位，复数域是目前已知最大的域

在复平面中，xx代表实数，yy轴（除原点外的点）代表虚数，从原点(0,0)(0,0)到(a,b)(a,b)的向量表示复数a+bia+bi

模长：从原点(0,0)(0,0)到点(a,b)(a,b)的距离，即a2+b2−−−−−−√a2+b2

幅角：假设以逆时针为正方向，从xx轴正半轴到已知向量的转角的有向角叫做幅角

C++的STL提供了复数模板！
头文件：#include <complex>
定义： complex<double> x;
运算：直接使用加减乘除。

代数定义：

(a+bi)∗(c+di)(a+bi)∗(c+di)

=ac+adi+bci+bdi2=ac+adi+bci+bdi2

=ac+adi+bci−bd=ac+adi+bci−bd

=(ac−bd)+(bc+ad)i

傅里叶要用到的n个复数，不是随机找的，而是——把单位圆（圆心为原点、1为半径的圆）n等分，取这n个点（或点表示的向量）所表示的虚数，即分别以这n个点的横坐标为实部、纵坐标为虚部，所构成的虚数。

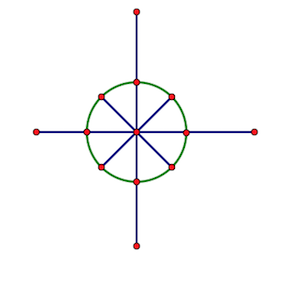
从点(1,0)(1,0)开始（显然这个点是我们要取的点之一），逆时针将这n个点从0开始编号，第kk个点对应的虚数记作ωnk（根据复数相乘时模长相乘幅角相加可以看出，ωnk是w1n的k次方，所以ω1n被称为n次单位根）。

单位根的性质

为什么要使用单位根作为xx代入

答：因为离散傅里叶变换有着特殊的性质。

一个结论

把多项式A(x)A(x)的离散傅里叶变换结果作为另一个多项式B(x)B(x)的系数，取单位根的倒数即ω0n,ω−1n,ω−2n,...,ω−(n−1)nωn0,ωn−1,ωn−2,...,ωn−(n−1)作为xx代入B(x)B(x)，得到的每个数再除以n，得到的是A(x)A(x)的各项系数

 

正主出场

快速傅里叶变换

然而知道了这些还不够（除非你想体验TLE的赶脚）

所以我们需要优化。

一.迭代优化（别问，问就是盗图，捂脸.jpg）

 

 

 

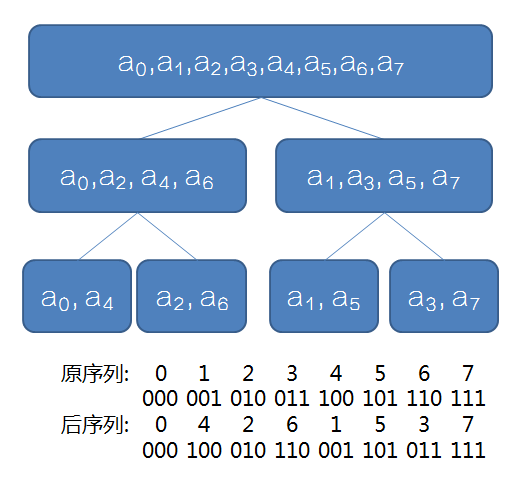
结论：每个位置分治后的最终位置为其二进制翻转后得到的位置
这样的话我们可以先把原序列变换好，把每个数放在最终的位置上，再一步一步向上合并
一句话就可以O(n)预处理第iii位最终的位置rev[i]

 

void get_rev(int bit){  //bit表示二进制的位数
    for(int i=0;i<(1<<bit);i++)//我么要对1~2^bit-1中的所有数做长度为bit的二进制翻转
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
}

emm我并没有看懂一开始，然后（我又要开始盗图啦）

我们可以把一个二进制数看成两部分，它的前bit-1位是一部分，它的最后一位是一部分。一个数的二进制翻转就相当于是把它的最后一位当成首位，然后在后面接上它前bit-1为的二进制翻转（有图有真相↓）。而且在这个循环中我们能保证，在计算“i”的二进制翻转之前1~i-1中的所有数的二进制翻转都已经完成。“i”的前bit-1位的数值其实就是[i/2]（向下取整）的值，也就是i>>1的值，直接调用i>>1的二进制翻转的结果就相当于调用了“i”的前bit-1位二进制翻转的结果。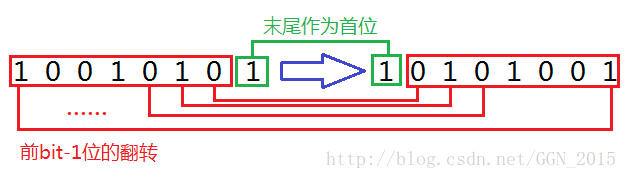

 

其实i>>1的翻转与“i”的前bit-1位的翻转是有一点出入的，因为我们的二进制翻转始终以bit位为标准，所以i>>1会比“i”的前bit-1位多出一个前导零，而翻转之后就会多出一个“后缀零”，所以“i”的前bit-1位的翻转要去掉那个“后缀零”，也就是“rev[i>>1]>>1”。

 

 

 

 

 我们只要把末尾乘上2^(bit-1)变成首位，再加上rev[i>>1]>>1就是我们要的答案了。（奇数偶数翻转的差别就是靠或操作来实现的）

二.蝴蝶操作（我又盗图了）

高不高大上？

 

 

好的，上述就是蝴蝶操作了（忘了它吧）这是一个很简单的优化

 他可以帮助你原地进行FFT的前一半更新后一半的操作，只需要对代码稍加改动（嗯，就一点点，真的）

优化完结撒花

---

 

例题：【模板】A*B Problem升级版（FFT快速傅里叶）

这边提供两种代码，一种是自己的，另一种嘛，是某金牌教练写的（我并咩有看懂）

#include<bits/stdc++.h>
using namespace std;
const int N=211314;
const double PI=acos(-1);
typedef complex<double>cp;
char sa[N],sb[N];
long long n=1,lena,lenb,res[N];
cp a[N],b[N],omg[N],inv[N];
void init(){
    for(int i=0;i<n;i++){
        omg[i]=cp(cos(2*PI*i/n),sin(2*PI*i/n));
        inv[i]=conj(omg[i]);//共轭函数 
    }    
}
void fft(cp *a, cp *omg){
    int lim = 0;
    while((1 << lim) < n) lim++;
    for(long long i = 0; i < n; i++){
        long long t = 0;
        for(long long j = 0; j < lim; j++)
            if((i >> j) & 1) t |= (1 << (lim - j - 1));
        if(i < t) swap(a[i], a[t]); 
    }
    for(long long l = 2; l <= n; l *= 2){
        int m = l / 2;
        for(cp *p = a; p != a + n; p += l)
            for(long long i = 0; i < m; i++){
                cp t = omg[n / l * i] * p[i + m];
                p[i + m] = p[i] - t;
                p[i] += t;
            }
        }
}
int main(){
    int l;cin>>l;  
    scanf("%s%s", sa, sb);
    lena = strlen(sa), lenb = strlen(sb);
    while(n < lena + lenb) n *= 2;
    for(long long i = 0; i < lena; i++)
        a[i].real(sa[lena - 1 - i] - '0');
    for(int i = 0; i < lenb; i++)
        b[i].real(sb[lenb - 1 - i] - '0');
    init();
    fft(a, omg);
    fft(b, omg);
    for(long long i = 0; i < n; i++)
        a[i] *= b[i];
    fft(a, inv);//inv是取共轭复数的符号
    for(long long i = 0; i < n; i++){
        res[i] += floor(a[i].real() / n + 0.5);
        res[i + 1] += res[i] / 10;
        res[i] %= 10;
    }
    int t=lena + lenb - 1;
    while(res[t]==0)t--; 
    for(int i =t; i >=0; i--){
        putchar('0'+res[i]);    
    } 
    putchar('\n');
    return 0;

}

 第二个（这是他在我们写高精度a+b的时候让我们做的题（我们才学了不到一个月啊！！！！））

#include <bits/stdc++.h>
using namespace std;
char s[60020];
long long a[14020];
long long b[14020];
long long c[14020];
int T = 9, B = 1;
int main() {
    scanf("%*d");
    for (int i = 0; i < T; i++) {
        B = B * 10;
    }
    scanf("%s", s);
    int la = strlen(s);
    reverse(s, s + la);
    for (int i = 0; i < la; i++) {
        s[i] -= '0';
    }
    for (int i = 0; i * T < la; i++) {
        for (int j = T - 1; j >= 0; j--) {
            a[i] = a[i] * 10 + s[i * T + j];
        }
    }
    la = (la + T - 1) / T;

    scanf("%s", s);
    int lb = strlen(s);
    reverse(s, s + lb);
    for (int i = 0; i < lb; i++) {
        s[i] -= '0';
    }
    for (int i = 0; i * T < lb; i++) {
        for (int j = T - 1; j >= 0; j--) {
            b[i] = b[i] * 10 + s[i * T + j];
        }
    }
    lb = (lb + T - 1) / T;
    int lc = la + lb;
    for (int i = 0; i < la; i++) {
        for (int j = 0; j < lb; j++) {
            c[i + j] += a[i] * b[j];
            c[i + j + 1] += c[i + j] / B;
            c[i + j] %= B;
        }
    }

    while (lc > 1 && c[lc - 1] == 0) {
        lc--;
    }

    printf("%d", (int)c[lc - 1]);
    for (int i = lc - 2; i >= 0; i--) {
        printf("%09d", (int)c[i]);
    }

    printf("\n");
    return 0;
}

 

二.【模板】多项式乘法（FFT）

这是一份被卡了两个点的代码（我不想改变我的写法（胡小兔大佬写法比较美观））

#include<bits/stdc++.h>
using namespace std;
const int N=5211314;
const double PI=acos(-1);
typedef complex<double>cp;
long long n=1,lena,lenb;
cp a[N],b[N],omg[N],inv[N];
void init(){
    for(int i=0;i<n;i++){
        omg[i]=cp(cos(2*PI*i/n),sin(2*PI*i/n));
        inv[i]=conj(omg[i]);//共轭函数 
    }    
}
void fft(cp *a, cp *omg){
    int lim = 0;
    while((1 << lim) < n) lim++;
    for(long long i = 0; i < n; i++){
        long long t = 0;
        for(long long j = 0; j < lim; j++)
            if((i >> j) & 1) t |= (1 << (lim - j - 1));
        if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次（否则交换两次相当于没交换）
    }
    for(long long l = 2; l <= n; l <<= 1){
        int m = l / 2;
        for(cp *p = a; p != a + n; p += l)
            for(long long i = 0; i < m; i++){
                cp t = omg[n / l * i] * p[i + m];
                p[i + m] = p[i] - t;
                p[i] += t;
            }
        }
}

int read(){
    int out = 0,flag = 1; char c = getchar();
    while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}
    while (c >= 48 && c <= 57) {out = (out << 3) + (out << 1) + c - '0'; c = getchar();}
    return out * flag;
}
int main(){ 
    lena=read();lenb=read();
    for(n=1;n<=lena+lenb;n<<=1);
    for(int i=0;i<=lena;i++)a[i]=read();
    for(int i=0;i<=lenb;i++)b[i]=read();
    init();
    fft(a,omg);
    fft(b,omg);
    for(int i=0;i<=n;i++)a[i]=a[i]*b[i];
    fft(a,inv);
    for(int i=0;i<=lena+lenb;i++)printf("%d ",(int)(a[i].real()/n+0.5));
    return 0;
} 

这是一份过了的代码

#include<bits/stdc++.h>
#define N 2621450
#define pi acos(-1)
using namespace std;
typedef complex<double> E;
int n,m,l,r[N];
E a[N],b[N];
void FFT(E *a,int f){
    for(int i=0;i<n;i++)if(i<r[i])swap(a[i],a[r[i]]);
    for(int i=1;i<n;i<<=1){
        E wn(cos(pi/i),f*sin(pi/i));
        for(int p=i<<1,j=0;j<n;j+=p){
            E w(1,0);
            for(int k=0;k<i;k++,w*=wn){
                E x=a[j+k],y=w*a[j+k+i];
                a[j+k]=x+y;a[j+k+i]=x-y;
            }
        }
    }
}
inline int read(){
    int f=1,x=0;char ch;
    do{ch=getchar();if(ch=='-')f=-1;}while(ch<'0'||ch>'9');
    do{x=x*10+ch-'0';ch=getchar();}while(ch>='0'&&ch<='9');
    return f*x;
}
int main(){
    n=read();m=read();
    for(int i=0;i<=n;i++)a[i]=read();
    for(int i=0;i<=m;i++)b[i]=read();
    m+=n;for(n=1;n<=m;n<<=1)l++;
    for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
    FFT(a,1);FFT(b,1);
    for(int i=0;i<=n;i++)a[i]=a[i]*b[i];
    FFT(a,-1);
    for(int i=0;i<=m;i++)printf("%d ",(int)(a[i].real()/n+0.5));
}

　完结。