分块学习笔记

先上大佬博客

也不知道为什么我先学的莫队

生动形象的分块（三层的树）

 

 

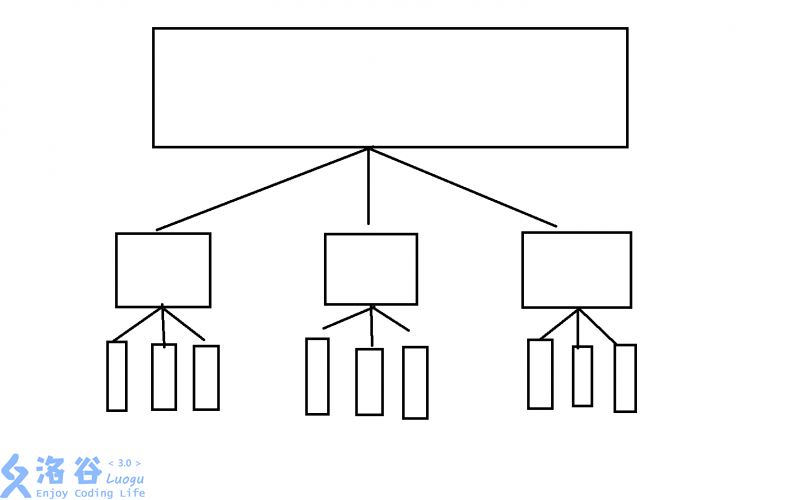
假设我们总共的序列长度为n，然后我们把它切成n−−√n块，然后把每一块里的东西当成一个整体来看，

现在解释几个本文用到的术语：

完整块：被操作区间完全覆盖的块

不完整块：操作区间不完全覆盖的块

然后我们先看看怎么得出答案：

　　1.对于完整的块，我们希望有个东西能直接找出这整个块的和，于是每个块要维护这个块的所有元素的和。   

　　  .对于不完整块，因为元素比较少(最多有  总数n /  块数 = n−−√n 个) 这时候当n=1000000的时候最多有1000个，对比一下，我们可以直接暴力扫这个小块统计答案，

　　  .小技巧：如果这个不完整块被覆盖的长度>块维护的长度的一半，何不用这个块的和-没有被覆盖的元素的值呢？

　　2.这里，我们换种思路，记录一个lazy   标记(为什么用lazy，因为我很懒),表示整个块被加上过多少了，

　　  .对于完整块，我们直接lazy+=加上的数x,块内的和ans+=x*元素个数(因为每个元素都被加上了x)

　　  .对于不完整块，直接暴力修改就好了，顺便可以把lazy标记清了。

题目列表

 

 

#6277. 数列分块入门 1

操作：区间加法，单点查值

#include <bits/stdc++.h>
using namespace std;
inline long long read() {  //读入优化
    long long x = 0;
    long long f = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')
            f = -f;
        c = getchar();
    }
    while (c <= '9' && c >= '0') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * f;
}
int n;
int m;
int opt, l, r, c;
int z[500521];    //原数组
int pos[500521];  //存储每个点所在的块
int tag[500521];  //标记数组
void modify(int l, int r, int c) {
    if (pos[l] == pos[r])  //如果在同一个块内直接暴力修改
        for (int i = l; i <= r; i++) z[i] += c;
    else {
        for (int i = l; i <= pos[l] * m; i++)  //修改左边不在一整块中的部分
            z[i] += c;
        for (int i = pos[l] + 1; i <= pos[r] - 1; i++)  //标记每个块需要加上的值
            tag[i] += c;
        for (int i = (pos[r] - 1) * m + 1; i <= r; i++)  //修改右边不在一整块中的部分
            z[i] += c;
    }
}
int main() {
    n = read();
    m = sqrt(n);
    for (int i = 1; i <= n; i++) z[i] = read();
    int bnum = ceil((double)n / m);  //上取整函数
    for (int i = 1; i <= bnum; i++)
        for (int j = (i - 1) * m + 1; j <= i * m; ++j) pos[j] = i;
    for (int i = 1; i <= n; i++) {
        opt = read();
        if (opt == 0) {
            l = read();
            r = read();
            c = read();
            modify(l, r, c);
        }
        if (opt == 1) {
            l = read();
            r = read();
            c = read();
            printf("%d\n",z[r] + tag[pos[r]]);  //最后输出的值就是该点的值加上该点所在块的标记值（即需要加上的值）
        }
    }
    return 0;
}

数列分块入门2：

操作：区间加法，询问区间内小于某个值 xxx 的元素个数

似乎并没有什么区别，主要就是多了一个reset函数，emm另外， lower_bound的特性利用也很重要

#include <bits/stdc++.h>
using namespace std;
inline long long read() {
    long long x = 0;
    long long f = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')
            f = -f;
        c = getchar();
    }
    while (c <= '9' && c >= '0') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * f;
}
long long n, m;
long long opt, l, r, c;
long long z[5211314];
long long pos[5211314];
long long tag[5211314];
vector<long long> v[1314];
void reset(long long x) {
    v[x].clear();  //清空该块内的元素
    for (long long i = (x - 1) * m + 1; i <= x * m; i++) v[x].push_back(z[i]);
    sort(v[x].begin(), v[x].end());
}
void modify(long long l, long long r, long long c) {  //修改函数
    if (pos[l] == pos[r]) {                           //在同一块内
        for (long long i = l; i <= r; i++)
            z[i] += c;  // 排序只是在vector中有序，因为是原数组修改，所以需要清空此块重新插入进行排序
        reset(pos[l]);
    } else {
        for (long long i = l; i <= pos[l] * m; i++)
            z[i] += c;  // 排序只是在vector中有序，因为是原数组修改，所以需要清空此块重新插入进行排序
        reset(pos[l]);
        for (long long i = pos[l] + 1; i <= pos[r] - 1; i++)
            tag[i] += c;  //对块进行标记时，区间加法并不会影响序列次序，所以只需要标记块
        for (long long i = (pos[r] - 1) * m + 1; i <= r; i++)
            z[i] += c;  // 排序只是在vector中有序，因为是原数组修改，所以需要清空此块重新插入进行排序
        reset(pos[r]);
    }
}

long long query(long long l, long long r, long long f) {
    long long ans = 0;
    if (pos[l] == pos[r]) {
        for (long long i = l; i <= r; i++)
            if (z[i] + tag[pos[i]] < f)
                ans++;
        return ans;
    } else {
        for (long long i = l; i <= pos[l] * m; i++)
            if (z[i] + tag[pos[i]] < f)
                ans++;
        for (long long i = pos[l] + 1; i <= pos[r] - 1; i++) {
            long long t = f - tag[i];
            // lowe_bound返回第一个大于或等于t的位置，减去begin得到区间内元素个数
            ans += lower_bound(v[i].begin(), v[i].end(), t) - v[i].begin();
        }
        for (long long i = (pos[r] - 1) * m + 1; i <= r; i++)
            if (z[i] + tag[pos[i]] < f)
                ans++;
    }
    return ans;
}
int main() {
    n = read();
    m = sqrt(n);
    //预处理每个点所在的快
    int bnum = ceil((double)n / m);  //上取整函数
    for (int i = 1; i <= bnum; i++)
        for (int j = (i - 1) * m + 1; j <= i * m; ++j) pos[j] = i;
    for (long long i = 1; i <= n; i++) {
        z[i] = read();
        v[pos[i]].push_back(z[i]);
    }
    //利用sort把每个块内的数据排好序 begin和end 代表所要排序的范围即整个v[i][~]‘’
    for (long long i = 1; i <= pos[n]; i++) sort(v[i].begin(), v[i].end());
    for (long long i = 1; i <= n; i++) {
        opt = read();
        if (opt == 0) {
            l = read();
            r = read();
            c = read();
            modify(l, r, c);
        }
        if (opt == 1) {
            l = read();
            r = read();
            c = read();
            printf("%lld\n", query(l, r, c * c));
        }
    }
    return 0;
}

 

　

数列分块入门 3

改一改查询操作就好了。

 

#include <bits/stdc++.h>
using namespace std;
inline long long read() {
    long long x = 0;
    long long f = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')
            f = -f;
        c = getchar();
    }
    while (c <= '9' && c >= '0') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * f;
}
long long n, m;
long long opt, l, r, c;
long long z[5211314];
long long pos[5211314];
long long tag[5211314];
vector<long long> v[1314];
void reset(long long x) {
    v[x].clear();  //清空该块内的元素
    for (long long i = (x - 1) * m + 1; i <= x * m; i++) v[x].push_back(z[i]);
    sort(v[x].begin(), v[x].end());
}
void modify(long long l, long long r, long long c) {  //修改函数
    if (pos[l] == pos[r]) {                           //在同一块内
        for (long long i = l; i <= r; i++)
            z[i] += c;  
        reset(pos[l]);
    } else {
        for (long long i = l; i <= pos[l] * m; i++)
            z[i] += c;  // 排序只是在vector中有序，因为是原数组修改，所以需要清空此块重新插入进行排序
        reset(pos[l]);
        for (long long i = pos[l] + 1; i <= pos[r] - 1; i++)
            tag[i] += c;  //对块进行标记时，区间加法并不会影响序列次序，所以只需要标记块
        for (long long i = (pos[r] - 1) * m + 1; i <= r; i++)
            z[i] += c;  // 排序只是在vector中有序，因为是原数组修改，所以需要清空此块重新插入进行排序
        reset(pos[r]);
    }
}

long long query(long long l, long long r, long long f) {
    long long ans = -1;
    if (pos[l] == pos[r]) {
        for (long long i = l; i <= r; i++)
            if (z[i] + tag[pos[i]] < c)
                ans=max(ans,z[i] + tag[pos[i]]);
        for (long long i = pos[l] + 1; i <= pos[r] - 1; i++) {
            long long t = c - tag[i];
            long long size=lower_bound(v[i].begin(), v[i].end(), t) - v[i].begin() ;
            if(size>=l&&size<=r)ans = max(v[i][size-1]+tag[i],ans);
        }
        return ans;
    } else {
        for (long long i = l; i <= pos[l] * m; i++)
            if (z[i] + tag[pos[i]] < c)
                ans=max(ans,z[i] + tag[pos[i]]); 
        for (long long i = (pos[r] - 1) * m + 1; i <= r; i++)
            if (z[i] + tag[pos[i]] < c)
                ans=max(ans,z[i] + tag[pos[i]]); 
        for (long long i = pos[l] + 1; i <= pos[r] - 1; i++) {
            long long t = c - tag[i];
            long long size=lower_bound(v[i].begin(), v[i].end(), t) - v[i].begin() ;
            if(size>=1)ans = max(v[i][size-1]+tag[i],ans);
        }
    }
    return ans;
}
int main() {
    n = read();
    m = sqrt(n);
    int bnum = ceil((double)n / m);
    for (int i = 1; i <= bnum; i++)
        for (int j = (i - 1) * m + 1; j <= i * m; ++j) pos[j] = i;
    for (long long i = 1; i <= n; i++) {
        z[i] = read();
        v[pos[i]].push_back(z[i]);
    }
    for (long long i = 1; i <= pos[n]; i++) sort(v[i].begin(), v[i].end());
    for (long long i = 1; i <= n; i++) {
        opt = read();
        if (opt == 0) {
            l = read();
            r = read();
            c = read();
            modify(l, r, c);
        }
        if (opt == 1) {
            l = read();
            r = read();
            c = read();
            printf("%lld\n", query(l, r, c));
        }
    }
    return 0;
}

 

数列分块入门4：

操作：区间加法，区间求和
操作还是不完整的块暴力，完整的标记区间，不过需要预处理出每个块的和。
修改时，修改每个点或块的同时，需要修改每个块的和

ps：注意数据范围数组需要开long long（简直毒瘤）

#include<bits/stdc++.h> 
using namespace std;
long long n,m;
const int maxn = 5211314;
long long pos[maxn],tag[maxn],sum[maxn],z[maxn];
long long opt, l, r, c;
long long ans;
inline long long read(){//读入优化
    long long x = 0; long long f = 1; char c = getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();}
    while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
void modify(long long l, long long r, long long c) {
    if (pos[l] == pos[r]) {
        for (int i = l; i <= r; i++) {
            z[i] +=c;
            sum[pos[i]]+=c ;
        }
    } else {
        for (int i = l; i <= pos[l] * m; i++) {
            z[i] +=c;
            sum[pos[i]]+=c ;
        }
        for (int i = (pos[r] - 1) * m + 1; i <= r; i++) {
            z[i] +=c;
            sum[pos[i]]+=c ;
        }
        for (int i = pos[l] + 1; i <= pos[r] - 1; i++) {
            tag[i]+=c;
            sum[i]+=m*c; 
        }
    }
}
long long query(long long l, long long r, long long c) {
    ans = 0;
    if (pos[l] == pos[r]) {
        for (int i = l; i <= r; i++) {
            ans += z[i] + tag[pos[l]];
        }
        return ans % c;
    } else {
        for (int i = l; i <= pos[l] * m; i++) {
            ans += z[i] + tag[pos[i]];
        }
        for (int i = (pos[r] - 1) * m + 1; i <= r; i++) {
            ans += z[i] + tag[pos[i]];
        }
        for (int i = pos[l] + 1; i <= pos[r] - 1; i++) {
            ans += sum[i];
        }
        return ans % c;
    }
}
int main(){
    n = read();
    m = sqrt(n);
    int bnum=ceil((double)n/m);//上取整函数 
    for(int i = 1; i <= bnum; i++) 
        for(int j=(i-1)*m+1;j<=i*m;++j)pos[j] = i;
    for(int i = 1; i<=n; i++) {z[i] = read();sum[pos[i]]+=z[i];}
    for(int i = 1; i<=n; i++){
         opt=read();
         if(opt == 0){
            l = read();
            r = read();
            c = read();
            modify(l,r,c);
         }
         if(opt == 1){
            l = read();
            r = read();
            c = read();
            printf("%lld\n",query(l,r,c+1));
         }
    }
    return 0;
}

 

数列分块入门5：

操作区间开方，区间求和

对于完整块，最多修改5次，因为前面分析过，修改5次肯定都为1了，所以上限为O(5n)。

对于不完整块，每次修改最多触及2次，所以上限为O(2n√n) 期间枚举完整块时间上限为O(n√n)。

上代码（我太爱loj的自动缩进了）

#include <bits/stdc++.h>
using namespace std;
const int N = 5211314;
int read() {
    int x = 0, k = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')
            k = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * k;
}
int opt, l, r, c, m, n;
int z[N], s[N], pos[N];
bool v[N];
void change(int l, int r) {
    if (pos[l] == pos[r]) {
        for (int i = l; i <= r; i++) {
            s[pos[i]] -= z[i];
            z[i] = sqrt(z[i]);
            s[pos[i]] += z[i];
        }
        return;
    } else {
        for (int i = l; i <= pos[l] * m; i++) {
            s[pos[i]] -= z[i];
            z[i] = sqrt(z[i]);
            s[pos[i]] += z[i];
        }
        for (int i = (pos[r] - 1) * m + 1; i <= r; i++) {
            s[pos[i]] -= z[i];
            z[i] = sqrt(z[i]);
            s[pos[i]] += z[i];
        }
        for (int i = pos[l] + 1; i <= pos[r] - 1; i++) {
            if (!v[i]) {
                v[i] = 1;
                for (int j = m * (i - 1) + 1; j <= m * i; j++) {
                    s[i] -= z[j];
                    z[j] = sqrt(z[j]);
                    s[i] += z[j];
                    if (z[j] > 1)
                        v[i] = 0;
                }
            }
        }
    }
}
int query(int l, int r) {
    int ans = 0;
    if (pos[l] == pos[r]) {
        for (int i = l; i <= r; i++) {
            ans += z[i];
        }
        return ans;
    } else {
        for (int i = l; i <= pos[l] * m; i++) {
            ans += z[i];
        }
        for (int i = (pos[r] - 1) * m + 1; i <= r; i++) {
            ans += z[i];
        }
        for (int i = pos[l] + 1; i <= pos[r] - 1; i++) {
            ans += s[i];
        }
        return ans;
    }
}
int main() {
    n = read(), m = sqrt(n);
    int bnum = ceil((double)n / m);
    for (int i = 1; i <= bnum; i++) {
        for (int j = m * (i - 1) + 1; j <= i * m; j++) {
            pos[j] = i;
        }
    }
    for (int i = 1; i <= n; i++) {
        z[i] = read();
        s[pos[i]] += z[i];
    }
    for (int i = 1; i <= n; i++) {
        opt = read();
        if (opt == 0) {
            l = read();
            r = read();
            c = read();
            change(l, r);
        }
        if (opt == 1) {
            l = read();
            r = read();
            c = read();
            printf("%lld\n", query(l, r));
        }
    }
}
　

 

数列分块入门6：
操作：单点插入，单点询问

用强大的vector解决这个问题

#include<bits/stdc++.h> 
using namespace std;
const int N=5211314;
long long read(){//读入优化
    long long x = 0; long long f = 1; char c = getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();}
    while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
int a[N]; 
int n,m,lx;
vector<int>v[1005];
void mer() {
    n=0;
    for(int i=1;i<=m+1;i++){
        if(v[i].empty())break;
        for(int j=0;j<v[i].size();j++){
            a[++n]=v[i][j]; 
        } 
        v[i].clear(); 
    }
} 
void div(){
    m=sqrt(n);
    int bnum=ceil((double)n/m);//上取整函数 
    for(int i = 1; i <= bnum; i++) 
        for(int j=(i-1)*m+1;j<=i*m;++j)v[i].push_back(a[j]);
} 
int query(int l){
    int bnum=ceil((double)n/m);
    for(int i=1;i<=bnum;i++){
        if(l>v[i].size())l-=v[i].size();
        else return v[i][l-1]; 
    } 
} 
void ins( int l, int c ){
    for ( int i = 1; i <= m + 1; ++i ){
        if ( l > v[i].size() ) l -= v[i].size();
        else{
            v[i].insert( v[i].begin() + l - 1, c );//插入~
            if ( v[i].size() > 10 * m ) mer(), div();//重排
            return;
        }
    }
}
int main(){
    n=read();
    for(int i=1;i<=n;i++)a[i]=read();
    div();
    lx=n;
    for(int i=1;i<=lx;i++){
        int opt,l,r,c;
        opt=read();
        if(opt==0){
           l=read(),r=read(),c=read(); 
           ins(l,r); 
        } else{
           l=read(),r=read(),c=read(); 
           printf("%d\n",query(r));
        } 
    } 
    return 0;
} 

 

 

 

数列分块入门7：

给出一个长为  的数列，以及  个操作，操作涉及区间乘法，区间加法，单点询问。

参考线段树的思想，将每一个点的值表示为a[i]=(a[i]*tagmul[pos[i]]+tadadd[pos[i]])%p,]照着前面的改就好了。

#include <bits/stdc++.h>
using namespace std;
#define N 5211314
const int p = 10007;
int n, m;
int a[N], pos[N], tagmul[N], tagadd[N];
int read() {
    int x = 0, k = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')
            k = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * k;
}
void push(int l) {
    for (int i = (l - 1) * m + 1; i <= l * m; i++) {
        a[i] = (a[i] * tagmul[l] + tagadd[l]) % p;
    }
    tagmul[l] = 1, tagadd[l] = 0;
}
void add(int l, int r, int c) {
    if (pos[l] == pos[r]) {
        push(pos[l]);
        for (int i = l; i <= r; i++) {
            a[i] = (a[i] + c) % p;
        }
        return;
    } else {
        push(pos[l]), push(pos[r]);
        for (int i = l; i <= pos[l] * m; i++) {
            a[i] = (a[i] + c) % p;
        }
        for (int i = (pos[r] - 1) * m + 1; i <= r; i++) {
            a[i] = (a[i] + c) % p;
        }
        for (int i = pos[l] + 1; i <= pos[r] - 1; i++) {
            tagadd[i] = (tagadd[i] + c) % p;
        }
    }
}
void mul(int l, int r, int c) {
    if (pos[l] == pos[r]) {
        push(pos[l]);
        for (int i = l; i <= r; i++) {
            a[i] = (a[i] * c) % p;
        }
        return;
    } else {
        push(pos[l]), push(pos[r]);
        for (int i = l; i <= pos[l] * m; i++) {
            a[i] = (a[i] * c) % p;
        }
        for (int i = (pos[r] - 1) * m + 1; i <= r; i++) {
            a[i] = (a[i] * c) % p;
        }
        for (int i = pos[l] + 1; i <= pos[r] - 1; i++) {
            tagadd[i] = (tagadd[i] * c) % p;
            tagmul[i] = (tagmul[i] * c) % p;
        }
    }
}
int main() {
    n = read();
    m = sqrt(n);
    int num = ceil((double)n / m);
    for (int i = 1; i <= num; i++) {
        for (int j = (i - 1) * m + 1; j <= i * m; j++) {
            pos[j] = i;
        }
    }
    for (int i = 1; i <= pos[n]; ++i) tagadd[i] = 0, tagmul[i] = 1;
    for (int i = 1; i <= n; i++) {
        a[i] = read();
    }
    for (int i = 1; i <= n; i++) {
        int opt = read(), l = read(), r = read(), c = read();
        switch (opt) {
            case 0:
                add(l, r, c);
                break;
            case 1:
                mul(l, r, c);
                break;
            case 2:
                printf("%d\n", (a[r] * tagmul[pos[r]] + tagadd[pos[r]]) % p);
                break;
        }
    }
    return 0;
}

数列分块入门8：

操作：操作涉及区间询问等于一个数 c 的元素，并将这个区间的所有元素改为 c

#include<bits/stdc++.h>
using namespace std;
#define N 5211314
int n,m;
int a[N],pos[N];
int v[N];
int read() {
    int x = 0, k = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')
            k = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * k;
}
void pushdown(int x){
    if(v[x]==-1) return ;
    for(int i=(x-1)*m+1;i<=min(n,x*m);i++) a[i]=v[x];
    v[x]=-1;    
}
int query(int l,int r,int c){
    int ans=0;
    pushdown(pos[l]);
    if(pos[l]==pos[r]){
       for(int i=l;i<=min(r,pos[l]*m);i++)    {
           if(a[i]==c) ans++;
           else a[i]=c; 
        }
    } 
    else {
        pushdown(pos[r]);
        for(int i=l;i<=min(r,pos[l]*m);i++)    {
           if(a[i]==c) ans++;
           else a[i]=c; 
        }
        for(int i=(pos[r]-1)*m+1;i<=r;i++) {
            if(a[i]==c) ans++;
            else a[i]=c;
        }
        for(int i=pos[l]+1;i<=pos[r]-1;i++){
        if(v[i]==-1){
            for(int j=(i-1)*m+1;j<=i*m;j++)
                if(a[j]==c) ans++;
        }
        if(v[i]==c) ans+=m;
        v[i]=c;
        }
    } 
    return ans;
} 
int main(){
    n=read();m=sqrt(n);
    int num=ceil((double)n/m);
    for(int i=1;i<=num;i++){
        v[i]=-1; 
        for(int j=(i-1)*m+1;j<=i*m;j++){
            pos[j]=i; 
        } 
    }
    for(int i=1;i<=n;i++)a[i]=read();
    for(int i=1;i<=n;i++){
        int l=read(),r=read(),c=read();
        printf("%d\n",query(l,r,c)); 
    } 
    return 0; 
} 

数列分块入门9

静态，区间求众数。

毒瘤题目我交了三页多

数据真是大的一批，样例也是水的一批怎么改都对。唉。毒瘤啊

#include<bits/stdc++.h>
using namespace std;
#define N 5211314
int n,m;
int a[N],pos[N];
int v[N];
int read() {
    int x = 0, k = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')
            k = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * k;
}
void pushdown(int x){
    if(v[x]==-1) return ;
    for(int i=(x-1)*m+1;i<=min(n,x*m);i++) a[i]=v[x];
    v[x]=-1;    
}
int query(int l,int r,int c){
    int ans=0;
    pushdown(pos[l]);
    if(pos[l]==pos[r]){
       for(int i=l;i<=min(r,pos[l]*m);i++)    {
           if(a[i]==c) ans++;
           else a[i]=c; 
        }
    } 
    else {
        pushdown(pos[r]);
        for(int i=l;i<=min(r,pos[l]*m);i++)    {
           if(a[i]==c) ans++;
           else a[i]=c; 
        }
        for(int i=(pos[r]-1)*m+1;i<=r;i++) {
            if(a[i]==c) ans++;
            else a[i]=c;
        }
        for(int i=pos[l]+1;i<=pos[r]-1;i++){
        if(v[i]==-1){
            for(int j=(i-1)*m+1;j<=i*m;j++)
                if(a[j]==c) ans++;
        }
        if(v[i]==c) ans+=m;
        v[i]=c;
        }
    } 
    return ans;
} 
int main(){
    n=read();m=sqrt(n);
    int num=ceil((double)n/m);
    for(int i=1;i<=num;i++){
        v[i]=-1; 
        for(int j=(i-1)*m+1;j<=i*m;j++){
            pos[j]=i; 
        } 
    }
    for(int i=1;i<=n;i++)a[i]=read();
    for(int i=1;i<=n;i++){
        int l=read(),r=read(),c=read();
        printf("%d\n",query(l,r,c)); 
    } 
    return 0; 
} 

分块完结。撒花~~。