莫队学习笔记

首先，贴上大佬的讲解WAMonster

然后大佬的卡常技巧一开始并没有看懂，经过多处查找。

下面的函数

int cmp(query a, query b) {
    return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}

等同于

int cmp(query a, query b) {//对于左端点在同一奇数块的区间，右端点按升序排列，反之降序
    return (belong[a.l]==belong[b.l]) ? ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r):belong[a.l] < belong[b.l] ;
}

然后饱受运算优先级折磨的我卑微的修改加上了注释（实在是看不懂）

while(l < ql) now -= (!--cnt[aa[l++]])/*del(l++)*/;//先cnt--，然后 ！，然后++ 
while(l > ql) now += (!cnt[aa[--l]]++)/*add(--l)*/;//先--l，然后！，然后++ 
while(r < qr) now += (!cnt[aa[++r]]++)/*add(++r)*/;//先++r，然后！，然后++ 
while(r > qr) now -= (!--cnt[aa[r--]])/*del(r--)*/;//先cnt--,然后！，然后--

然后全部代码（并没有什么改动）

#include<bits/stdc++.h>
using namespace std;
#define maxn 1010000
#define maxb 1010
#define isdigit(x) ((x) >= '0' && (x) <= '9')
int aa[maxn], cnt[maxn], belong[maxn];
int n, m, size, bnum, now, ans[maxn];
struct query {
    int l, r, id;
} q[maxn];
int cmp(query a, query b) {//对于左端点在同一奇数块的区间，右端点按升序排列，反之降序
    return (belong[a.l]==belong[b.l]) ? ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r):belong[a.l] < belong[b.l] ;
}
/*void add(int pos) {
    if(!cnt[aa[pos]]) ++now;
    ++cnt[aa[pos]];
}
void del(int pos) {
    --cnt[aa[pos]];
    if(!cnt[aa[pos]]) --now;
}*/
int read() {
    int res = 0;
    char c = getchar();
    while(!isdigit(c)) c = getchar();
    while(isdigit(c)) res = (res << 1) + (res << 3) + c - 48, c = getchar();
    return res;
}
void printi(int x) {
    if(x / 10) printi(x / 10);
    putchar(x % 10 + '0');
}
int main() {
    scanf("%d", &n);
    size = sqrt(n);
    bnum =ceil((double)n / size);
    for(int i = 1; i <= bnum; ++i) 
        for(int j = (i - 1) * size + 1; j <= i * size;j++) {
            belong[j] = i;
        }
    for(int i = 1; i <= n; ++i) aa[i] = read(); 
    m = read();
    for(int i = 1; i <= m; ++i) {
        q[i].l = read(), q[i].r = read();
        q[i].id = i;
    }
    sort(q + 1, q + m + 1, cmp);
    int l = 1, r = 0;
    for(int i = 1; i <= m; ++i) {
        int ql = q[i].l, qr = q[i].r;
        while(l < ql) now -= (!--cnt[aa[l++]])/*del(l++)*/;//先cnt--，然后 ！，然后++ 
        while(l > ql) now += (!cnt[aa[--l]]++)/*add(--l)*/;//先--l，然后！，然后++ 
        while(r < qr) now += (!cnt[aa[++r]]++)/*add(++r)*/;//先++r，然后！，然后++ 
        while(r > qr) now -= (!--cnt[aa[r--]])/*del(r--)*/;//先cnt--,然后！，然后-- 
        ans[q[i].id] = now;
    }
    for(int i = 1; i <= m; ++i) printi(ans[i]), putchar('\n');
    return 0;
}

 

接下来出场的是可修改莫队

好题（毒瘤）

这题似乎加强了数据搞的必须开O2才能过（题解里的神仙解法例外）

普通莫队要离线下来做，遇到这种带修改的题目直接就萎了，但是全国广大的OIer们在莫队的基础上，发明了带修莫队这种玄学算法。

对于某些允许离线的带修改区间查询来说，莫队还是能大展拳脚的。做法就是把莫队直接加上一维，变为带修莫队。

具体来说就是给修改和求值打上时间戳，然后在普通莫队双指针的基础上增加一个指针time指向时间，在这一个维度上面跳来跳去，直到跳到左指针指向左端点，右指针指向右端点，time指针指向当前求值的时间戳为止。

通俗地讲，就是再弄一指针，在修改操作上跳来跳去，如果当前修改多了就改回来，改少了就改过去，直到次数恰当为止。(来自大佬的言简意赅)Orz

带修改莫队的排序：

其实排序的主要方法还是跟普通莫队没两样，只不过是加了个关键字而已。

排序函数：

int cmp(ask a,ask b) {
    return (belong[a.l]==belong[b.l])?((belong[a.r]==belong[b.r])?a.time<b.time:belong[a.r]<belong[b.r]):belong[a.l]<belong[b.l];
}

主算法中的修改操作

似乎与原来的修改区别不大，但值得一提的是，在修改的时候，由于我们的time指针可能“往回跳”，所以我们要记下来之前的值，因此我们可以直接swap这俩值，回来的时候就直接swap回来。(存下来也可以吧)

分块大小和复杂度

大佬证明：

块大小为  可以达到最快的理论复杂度  ，证明如下

设分块大小为a，莫队算法时间复杂度主要为t轴移动，同r块l,r移动，l块间的r移动三部分

t轴移动的复杂度为  ，同r块l,r移动复杂度为  ，l块间的r移动复杂度为 

三个函数max的最小值当a为  取得，为 

证明了当块的大小设n4t−−−√3n4t3时理论复杂度达到最优，而块大小取n−−√n时会退化成O(n2)O(n2)，不建议使用。

然后就是毒瘤题的代码了并没有什么改动

#include<bits/stdc++.h>
using namespace std;
#define maxn 1333340//毒瘤题数据加强了
#define maxc 1001000
int a[maxn],cnt[maxc],ans[maxn],belong[maxn];
struct ask{
    int l, r, time, id;
} q[maxn];
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9')ch=getchar();
    while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    return x*f;
}
struct modify{
    int pos,color,last;
} c[maxn];
int cntq, cntc, n, m, size, bnum;
int cmp(ask a,ask b) {
    return (belong[a.l]==belong[b.l])?((belong[a.r]==belong[b.r])?a.time<b.time:belong[a.r]<belong[b.r]):belong[a.l]<belong[b.l];
}
int main() {
    n=read(),m=read();
    size=pow(n,2.0/3.0);
    bnum=ceil((double)n/size);//上取整函数 
    for(int i = 1; i <= bnum; ++i) 
        for(int j=(i-1)*size+1;j<=i*size;++j)belong[j] = i;
    for(int i = 1; i <= n; ++i) 
        a[i] = read();
    for(int i = 1; i <= m; ++i) {
        char opt;
        opt=getchar();getchar(); 
        if(opt == 'Q') {
            q[++cntq].l=read();
            q[cntq].r=read();
            q[cntq].time=cntc;
            q[cntq].id =cntq;
        }
        else if(opt == 'R') {
            c[++cntc].pos=read();
            c[cntc].color=read();
        }
    }
    sort(q + 1, q + cntq + 1, cmp);
    int l = 1, r = 0, time = 0, now = 0;
    for(int i = 1; i <= cntq; ++i) {
        int ql = q[i].l, qr = q[i].r, qt = q[i].time;
        while(l<ql) now-= (!--cnt[a[l++]]);
        while(l>ql) now+= (!cnt[a[--l]]++);
        while(r<qr) now+= (!cnt[a[++r]]++);
        while(r>qr) now-= (!--cnt[a[r--]]);
        while(time < qt) {
            ++time;
            if(ql <= c[time].pos && c[time].pos <= qr) now -= (!--cnt[a[c[time].pos]] - !cnt[c[time].color]++);
            swap(a[c[time].pos], c[time].color);
        }
        while(time > qt) {
            if(ql <= c[time].pos && c[time].pos <= qr) now -= (!--cnt[a[c[time].pos]] - !cnt[c[time].color]++);
            swap(a[c[time].pos], c[time].color);
            --time;
        }
        ans[q[i].id] = now;
    }
    for(int i = 1; i <= cntq; ++i) 
        printf("%d\n", ans[i]);
    return 0;
}

 

莫队算法的扩展——树上莫队

路径上的统计

题目

分析：

 

 

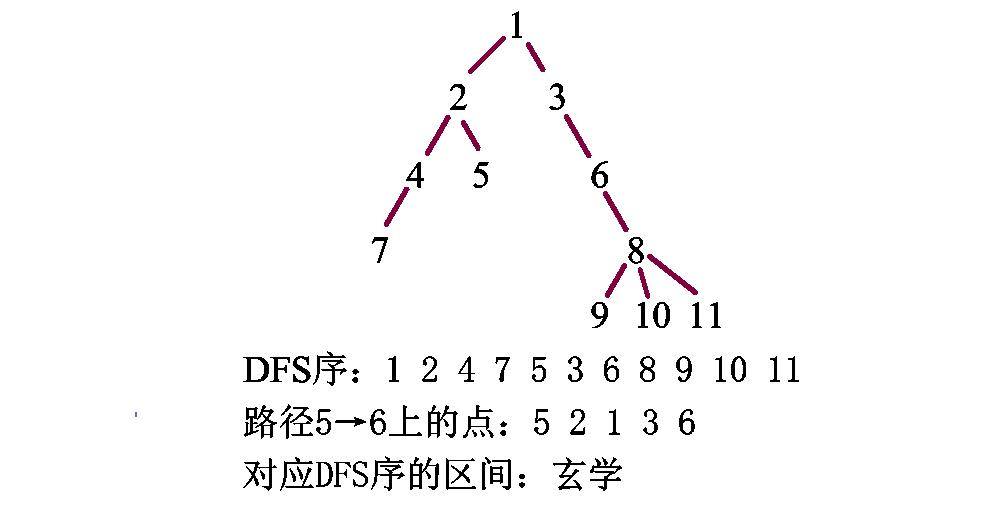
 简单的DFS序并不能满足我们进行莫队的应用，因此我们需要用神奇的欧拉序图二来表示。

 结论：树的欧拉序上两个相同编号（设为xx）之间的所有编号都出现两次，且都位于xx子树上Orz

 

 

大佬对于经过点是否加入答案的解释：树上路径的定义为：从xx到yy经过节点个数最少的路径。

若一个点kk出现两次，说明我们可以先访问kk，进入kk的子树中，然后出来，再到yy，很显然不访问kk是更优的。因此出现两次的点不能统计入答案

 

WAMonster大佬的具体做法非常详细：设每个点的编号aa首次出现的位置first[a]first[a]，最后出现的位置为last[a]last[a]，那么对于路径x→yx→y，设first[x]<=first[y]first[x]<=first[y]

（不满足则swap，这个操作的意义在于，如果xx、yy在一条链上，则xx一定是yy的祖先或等于yy），如果lca(x,y)=xlca(x,y)=x，则直接把[first[x],first[y]][first[x],first[y]]的区间扯过来用

，反之使用[last[x],first[y]][last[x],first[y]]区间（为什么不用[first[x],first[y]][first[x],first[y]]？因为(first[x],last[x])(first[x],last[x])不会在路径上，根据性质，里面的编号都会出现两次，考虑了等于没考虑），

但这个区间内不包含xx和yy的最近公共祖先，查询的时候加上即可。

 

注意：序列长度要*2避免越界

#include<bits/stdc++.h>
using namespace std;
#define maxn 200200
#define isdigit(x) ((x) >= '0' && (x) <= '9')
inline int read() {
    int res = 0;
    char c = getchar();
    while(!isdigit(c)) c = getchar();
    while(isdigit(c)) res = (res << 1) + (res << 3) + (c ^ 48), c = getchar();
    return res;
}
int aa[maxn], cnt[maxn], first[maxn], last[maxn], ans[maxn];
int belong[maxn], inp[maxn], vis[maxn], ncnt, l = 1, r, now, size, bnum; //莫队相关
int ord[maxn], val[maxn], head[maxn], depth[maxn], fa[maxn][30], ecnt;
int n, m;
struct edge {
    int to, next;
} e[maxn];
void adde(int u, int v) {
    e[++ecnt] = (edge){v, head[u]};
    head[u] = ecnt;
    e[++ecnt] = (edge){u, head[v]};
    head[v] = ecnt;
}
void dfs(int x) {
    ord[++ncnt] = x;
    first[x] = ncnt;
    for(int k = head[x]; k; k = e[k].next) {
        int to = e[k].to;
        if(to == fa[x][0]) continue;
        depth[to] = depth[x] + 1;
        fa[to][0] = x;
        for(int i = 1;(1 << i)<=depth[to]; ++i)
            fa[to][i] = fa[fa[to][i - 1]][i - 1];
        dfs(to);
    }
    ord[++ncnt] = x;
    last[x] = ncnt;
}
int getlca(int x, int y) {
    if (depth[x] < depth[y]) {
        swap(x, y);
    }
    int dd = depth[x] - depth[y];
    for (int i = 0; i < 20; i++) {
        if (dd >> i & 1) {
            x = fa[x][i];
        }
    }
    if (x == y) {
        return x;
    }
    for (int i = 20 - 1; i >= 0; i--) {
        if (fa[x][i] != fa[y][i]) {
            x = fa[x][i];
            y = fa[y][i];
        }
    }
    return fa[x][0];
}
struct query {
    int l, r, lca, id;
} q[maxn];
int cmp(query a, query b) {//对于左端点在同一奇数块的区间，右端点按升序排列，反之降序
    return (belong[a.l]==belong[b.l]) ? ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r):belong[a.l] < belong[b.l] ;
}
void work(int pos) {
    vis[pos] ? now -= !--cnt[val[pos]] : now += !cnt[val[pos]]++;
    vis[pos] ^= 1;//不进位加法，重复两次的点不记入答案 
}
int main() {
    n = read(); m = read();
    for(int i = 1; i <= n; ++i) 
        val[i] = inp[i] = read();
    sort(inp + 1, inp + n + 1);
    int tot = unique(inp + 1, inp + n + 1) - inp - 1;
    for(int i = 1; i <= n; ++i)
        val[i] = lower_bound(inp + 1, inp + tot + 1, val[i]) - inp;
    for(int i = 1; i < n; ++i) adde(read(), read());
    depth[1] = 1;
    dfs(1);
    size = sqrt(ncnt), bnum = ceil((double) ncnt / size);
    for(int i = 1; i <= bnum; ++i)
        for(int j = size * (i - 1) + 1; j <= i * size; ++j) belong[j] = i;
    for(int i = 1; i <= m; ++i) {
        int L = read(), R = read(), lca = getlca(L, R);
        if(first[L] > first[R]) swap(L, R);
        if(L == lca) {
            q[i].l = first[L];
            q[i].r = first[R];
        }
        else {
            q[i].l = last[L];
            q[i].r = first[R];
            q[i].lca = lca;
        }
        q[i].id = i;
    }
    sort(q + 1, q + m + 1, cmp);
    for(int i = 1; i <= m; ++i) {
        int ql = q[i].l, qr = q[i].r, lca = q[i].lca;
        while(l < ql) work(ord[l++]);
        while(l > ql) work(ord[--l]);
        while(r < qr) work(ord[++r]);
        while(r > qr) work(ord[r--]);
        if(lca) work(lca);
        ans[q[i].id] = now;
        if(lca) work(lca);//消除掉本次操作的影响避免对下一次查询区间的影响 
    }
    for(int i = 1; i <= m; ++i) printf("%d\n", ans[i]);
    return 0;
}