redis常用数据类型 HyperLoglog

 

1.HyperLoglog简介

HyperLoglog是redis新支持的两种类型中的另外一种(上一种是位图类型Bitmaps)。主要适用场景是海量数据的计算。特点是速度快。占用空间小。

同样是用于计算，HyperLoglog在适用场景方面与Bitmaps方面有什么不同呢。我个人的理解是，Bitmaps更适合用于验证的大数据，比如签到，

记录某用户是不是当天进行了签到，签到了多少天的时候。也就是说，你不光需要记录数据，还需要对数据进行验证的时候使用Bitmaps。

HyperLoglog则用于只记录的时候，比如访问的uv统计。

2.HyperLoglog相关命令

（1）

命令：PFADD key element [element ...]

时间复杂度：O(1)

命令描述：将除了第一个参数以外的参数存储到以第一个参数为变量名的HyperLogLog结构中。这个命令的一个副作用是它可能会更改这个HyperLogLog的内部来反映在每添加一个唯一的对象时估计的基数(集合的基数)。如果一个HyperLogLog的估计的近似基数在执行命令过程中发了变化， PFADD返回1，否则返回0，如果指定的key不存在，这个命令会自动创建一个空的HyperLogLog结构（指定长度和编码的字符串）。如果在调用该命令时仅提供变量名而不指定元素也是可以的，如果这个变量名存在，则不会有任何操作，如果不存在，则会创建一个数据结构。

返回值：如果 HyperLogLog 的内部被修改了,那么返回 1,否则返回 0 。

 

（2）

命令：PFCOUNT key [key ...]

命令描述：当参数为一个key时,返回存储在HyperLogLog结构体的该变量的近似基数，如果该变量不存在,则返回0。当参数为多个key时，返回这些HyperLogLog并集的近似基数，这个值是将所给定的所有key的HyperLoglog结构合并到一个临时的HyperLogLog结构中计算而得到的。HyperLogLog可以使用固定且很少的内存（每个HyperLogLog结构需要12K字节再加上key本身的几个字节）来存储集合的唯一元素。返回的可见集合基数并不是精确值， 而是一个带有 0.81% 标准错误（standard error）的近似值。

返回值：PFADD添加的唯一元素的近似数量。

 

（3）

命令：PFMERGE destkey sourcekey [sourcekey ...]

命令描述：将多个 HyperLogLog 合并（merge）为一个 HyperLogLog ， 合并后的 HyperLogLog 的基数接近于所有输入 HyperLogLog 的可见集合（observed set）的并集。合并得出的 HyperLogLog 会被储存在目标变量（第一个参数）里面， 如果该键并不存在， 那么命令在执行之前， 会先为该键创建一个空的。

返回值：这个命令只会返回 OK。

 

Redis HyperLogLog

 

 

Redis HyperLogLog 是用来做基数统计的算法，HyperLogLog 的优点是，在输入元素的数量或者体积非常非常大时，计算基数所需的空间总是固定 的、并且是很小的。

在 Redis 里面，每个 HyperLogLog 键只需要花费 12 KB 内存，就可以计算接近 2^64 个不同元素的基 数。这和计算基数时，元素越多耗费内存就越多的集合形成鲜明对比。

但是，因为 HyperLogLog 只会根据输入元素来计算基数，而不会储存输入元素本身，所以 HyperLogLog 不能像集合那样，返回输入的各个元素。

---

什么是基数?

比如数据集 {1, 3, 5, 7, 5, 7, 8}， 那么这个数据集的基数集为 {1, 3, 5 ,7, 8}, 基数(不重复元素)为5。 基数估计就是在误差可接受的范围内，快速计算基数。

---

 

pfadd key element [element...] 将所有元素参数添加到 HyperLogLog 数据结构中,如果至少有个元素被添加返回 1， 否则返回 0

pfcount key [key...] 返回给定 HyperLogLog 的基数估算值。返回给定 HyperLogLog 的基数值，如果多个 HyperLogLog 则返回基数估值之和

pfmerge destkey sourcekey [sourcekey...] 将多个 HyperLogLog 合并为一个 HyperLogLog ，合并后的 HyperLogLog 的基数估算值是通过对所有 给定 HyperLogLog 进行并集计算得出的。

 

 

 

基数的应用实例

下面通过一个实例说明基数在电商数据分析中的应用。

假设一个淘宝网店在其店铺首页放置了10个宝贝链接，分别从Item01到Item10为这十个链接编号。店主希望可以在一天中随时查看从今天零点开始到目前这十个宝贝链接分别被多少个独立访客点击过。所谓独立访客（Unique Visitor，简称UV）是指有多少个自然人，例如，即使我今天点了五次Item01，我对Item01的UV贡献也是1，而不是5。

用术语说这实际是一个实时数据流统计分析问题。

要实现这个统计需求。需要做到如下三点：

1、对独立访客做标识

2、在访客点击链接时记录下链接编号及访客标记

3、对每一个要统计的链接维护一个数据结构和一个当前UV值，当某个链接发生一次点击时，能迅速定位此用户在今天是否已经点过此链接，如果没有则此链接的UV增加1

下面分别介绍三个步骤的实现方案

对独立访客做标识

客观来说，目前还没有能在互联网上准确对一个自然人进行标识的方法，通常采用的是近似方案。例如通过登录用户+cookie跟踪的方式：当某个用户已经登录，则采用会员ID标识；对于未登录用户，则采用跟踪cookie的方式进行标识。为了简单起见，我们假设完全采用跟踪cookie的方式对独立访客进行标识。

记录链接编号及访客标记

这一步可以通过JavaScript埋点及记录accesslog完成，具体原理和实现方案可以参考我之前的一篇文章：网站统计中的数据收集原理及实现。

实时UV计算

可以看到，如果将每个链接被点击的日志中访客标识字段看成一个集合，那么此链接当前的UV也就是这个集合的基数，因此UV计算本质上就是一个基数计数问题。

在实时计算流中，我们可以认为任何一次链接点击均触发如下逻辑（伪代码描述）：

1. cand_counting(item_no, user_id) {
2. if (user_id is not in the item_no visitor set) {
3. add user_id to item_no visitor set;
4. cand[item_no]++;
5. }
6. }

逻辑非常简单，每当有一个点击事件发生，就去相应的链接被访集合中寻找此访客是否已经在里面，如果没有则将此用户标识加入集合，并将此链接的UV加1。

虽然逻辑非常简单，但是在实际实现中尤其面临大数据场景时还是会遇到诸多困难，下面一节我会介绍两种目前被业界普遍使用的精确算法实现方案，并通过分析说明当数据量增大时它们面临的问题。

传统的基数计数实现

接着上面的例子，我们看一下目前常用的基数计数的实现方法。

基于B树的基数计数

对上面的伪代码做一个简单分析，会发现关键操作有两个：查找-迅速定位当前访客是否已经在集合中，插入-将新的访客标识插入到访客集合中。因此，需要为每一个需要统计UV的点（此处就是十个宝贝链接）维护一个查找效率较高的数据结构，又因为实时数据流的关系，这个数据结构需要尽量在内存中维护，因此这个数据结构在空间复杂度上也要比较适中。综合考虑一种传统的做法是在实时计算引擎采用了B树来组织这个集合。下图是一个示意图：

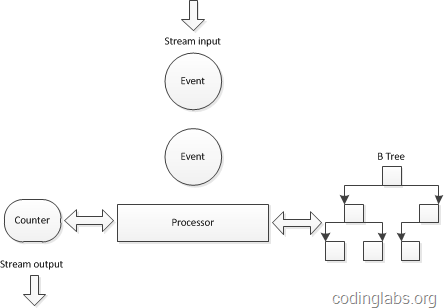
之所以选用B树是因为B树的查找和插入相关高效，同时空间复杂度也可以接受（关于B树具体的性能分析请参考这里）。

这种实现方案为一个基数计数器维护一棵B树，由于B树在查找效率、插入效率和内存使用之间非常平衡，所以算是一种可以接受的解决方案。但是当数据量特别巨大时，例如要同时统计几万个链接的UV，如果要将几万个链接一天的访问记录全部维护在内存中，这个内存使用量也是相当可观的（假设每个B树占用1M内存，10万个B树就是100G！）。一种方案是在某个时间点将内存数据结构写入磁盘（双十一和双十二大促时一淘数据部的效果平台是每分钟将数据写入HBase）然后将内存中的计数器和数据结构清零，但是B树并不能高效的进行合并，这就使得内存数据落地成了非常大的难题。

另一个需要数据结构合并的场景是查看并集的基数，例如在上面的例子中，如果我想查看Item1和Item2的总UV，是没有办法通过这种B树的结构快速得到的。当然可以为每一种可能的组合维护一棵B树。不过通过简单的分析就可以知道这个方案基本不可行。N个元素集合的非空幂集数量为2N−1，因此要为10个链接维护1023棵B树，而随着链接的增加这个数量会以幂指级别增长。

基于bitmap的基数计数

为了克服B树不能高效合并的问题，一种替代方案是使用bitmap表示集合。也就是使用一个很长的bit数组表示集合，将bit位顺序编号，bit为1表示此编号在集合中，为0表示不在集合中。例如“00100110”表示集合 {2，5，6}。bitmap中1的数量就是这个集合的基数。

显然，与B树不同bitmap可以高效的进行合并，只需进行按位或（or）运算就可以，而位运算在计算机中的运算效率是很高的。但是bitmap方式也有自己的问题，就是内存使用问题。

很容易发现，bitmap的长度与集合中元素个数无关，而是与基数的上限有关。例如在上面的例子中，假如要计算上限为1亿的基数，则需要12.5M字节的bitmap，十个链接就需要125M。关键在于，这个内存使用与集合元素数量无关，即使一个链接仅仅有一个1UV，也要为其分配12.5M字节。

由此可见，虽然bitmap方式易于合并，却由于内存使用问题而无法广泛用于大数据场景。

小结

本文重点在于通过电商数据分析中UV计算的例子，说明基数的应用、传统的基数计数算法及这些算法在大数据面前遇到的问题。实际上目前还没有发现更好的在大数据场景中准确计算基数的高效算法，因此在不追求绝对准确的情况下，使用概率算法算是一个不错的解决方案。在后续文章中，我将逐一解读常用的基数估计概率算法。

转载请注明原处