二叉树基础知识小结

一，树的定义

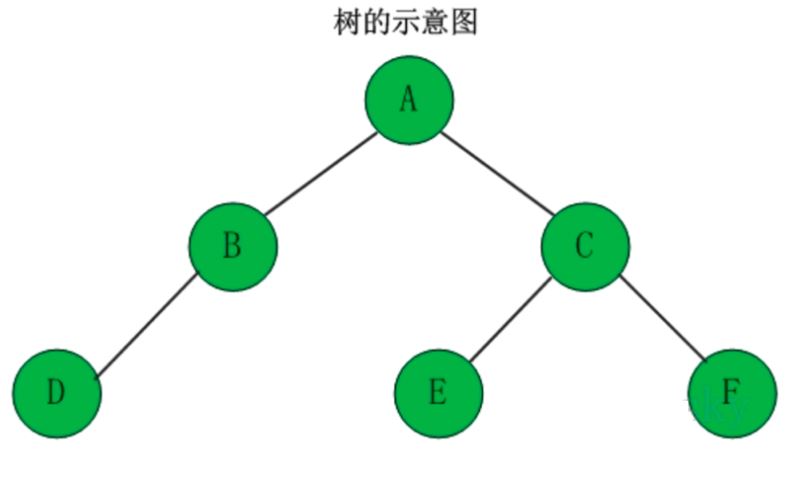
树是一种数据结构，他是由n(n >= 1)个有限结点组成一个具有层次关系的集合。

 

 

 

 

 

树具有的特点有：

（1）每个结点有零个或多个子结点

（2）没有父节点的结点称为根节点

（3）每一个非根结点有且只有一个父节点

（4）除了根结点外，每个子结点可以分为多个不相交的子树。（如果是二叉树，那么子节点最多是 2个。）

 

 

 

树的基本术语有：

 

 

若一个结点有子树，那么该结点称为子树根的“双亲”，子树的根称为该结点的“孩子”。有相同双亲的结点互为“兄弟”。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。

 

结点的度：结点拥有的子树的数目

叶子结点：度为0的结点

分支结点：度不为0的结点

树的度：树中结点的最大的度

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1

树的高度：树中结点的最大层次

森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

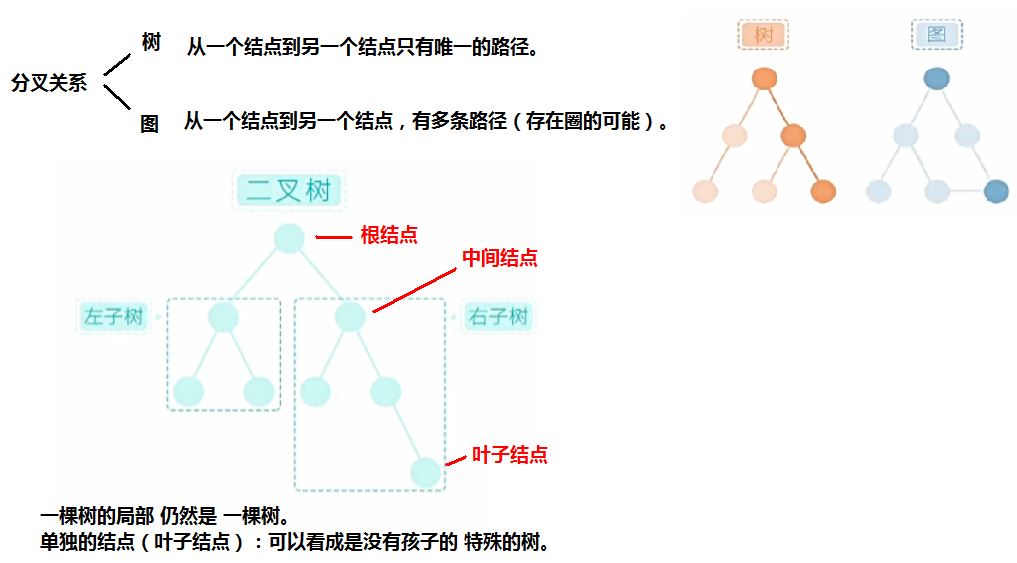
二、二叉树

1、二叉树的定义

 

 

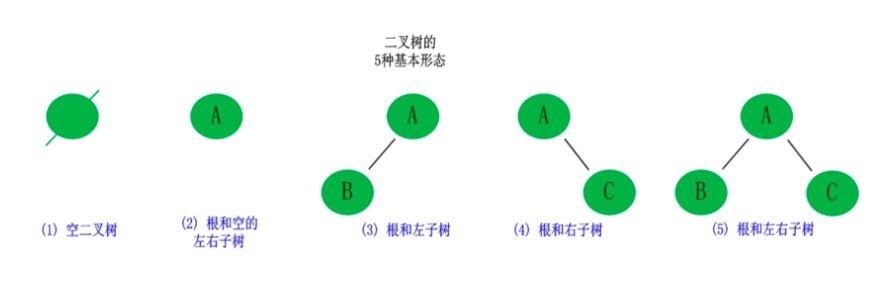
二叉树是每个结点最多有两个子树的树结构。

它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左、右子树皆为空。

 

 

 

 

 

2、二叉树的性质

性质1：二叉树第 i 层上的结点数目最多为 2^i-1 (i>=1)

性质2：深度为k的二叉树至多有2^k-1个结点（k>=1）

性质3：包含n个结点的二叉树的高度至少为[(log₂n)+1]。 （其中[ ]是取整函数）

性质4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1 。（可以通过实例来说明）

3、性质4的证明

性质4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1

证明：因为二叉树中所有结点的度数均不大于2，不妨设n₀表示度为0的结点个数，n₁表示度为1的结点个数，n₂表示度为2的结点个数。三类结点加起来为总结点个数，于是便可得到：n=n₀+n₁+n₂  (1)

由度之间的关系可得第二个等式：n=n₀*0+n₁*1+n₂*2+1，即n=n₁+2n₂+1  (2)  （注意：+1 是加上 根结点）

将（1）（2）组合在一起可得到n₀=n₂+1

三、满二叉树、完全二叉树和二叉查找树

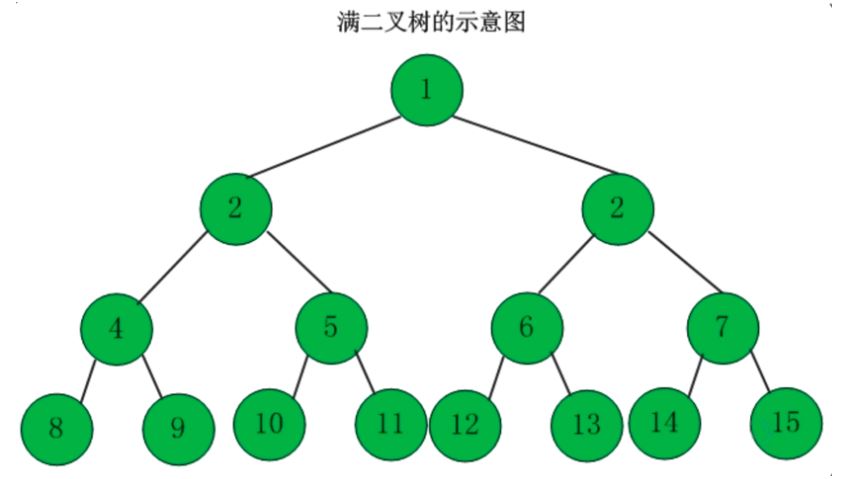
1、满二叉树

定义：高度为h，并且由2^h-1个结点组成的二叉树，称为满二叉树

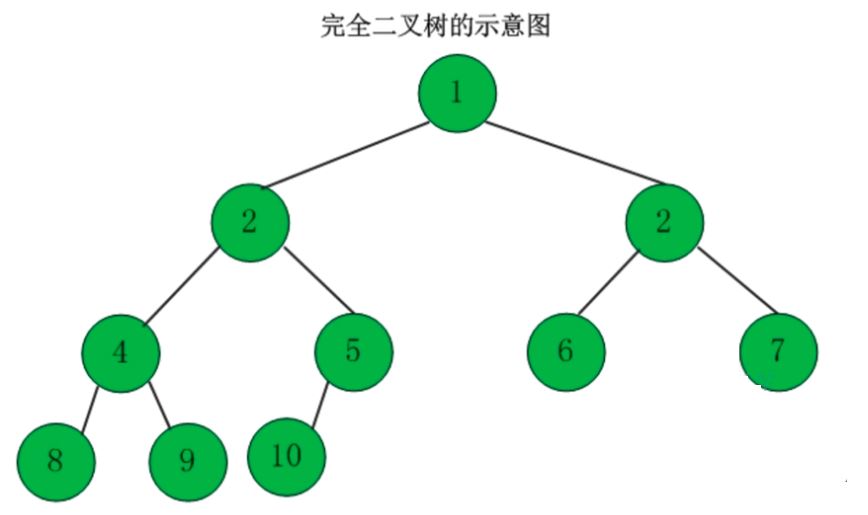
2、完全二叉树

定义：一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下层的叶结点集中在靠左的若干位置上，这样的二叉树称为完全二叉树。

特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

面试题：如果一个完全二叉树的结点总数为768个，求叶子结点的个数。

由二叉树的性质知：n₀=n₂+1，将之带入768=n₀+n₁+n₂中得：768=n₁+2n₂+1，因为完全二叉树度为1的结点个数要么为0，要么为1，那么就把n₁=0或者1都代入公式中，很容易发现n₁=1才符合条件。所以算出来n₂=383，所以叶子结点个数n₀=n₂+1=384。

总结规律：如果一棵完全二叉树的结点总数为n，那么叶子结点等于n/2（当n为偶数时）或者(n+1)/2（当n为奇数时）

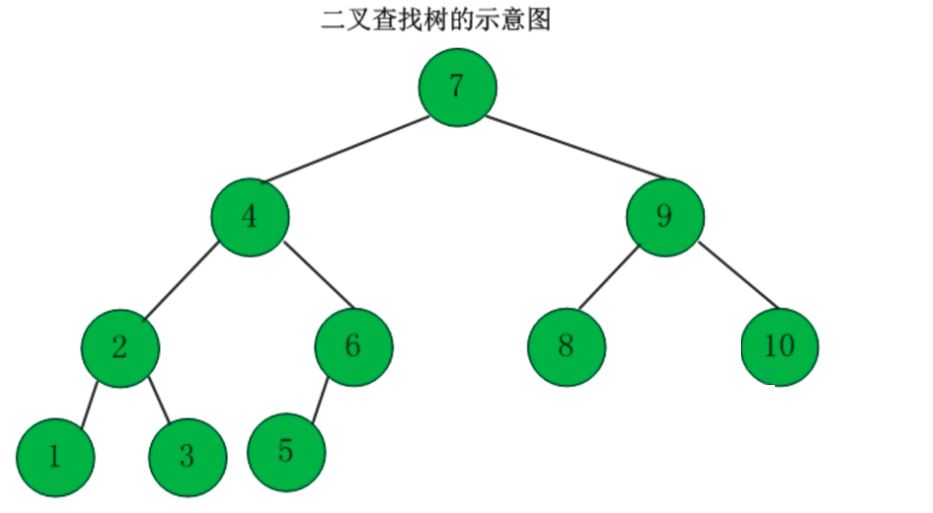
3、二叉查找树

定义：二叉查找树又被称为二叉搜索树。设x为二叉查找树中的一个结点，x结点包含关键字key，结点x的key值计为key[x]。如果y是x的左子树中的一个结点，则key[y]<=key[x]；如果y是x的右子树的一个结点，则key[y]>=key[x]

 

 

 

 

在二叉查找树种：

（1）若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。

（2）任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。

（3）任意结点的左、右子树也分别为二叉查找树。

（4）没有键值相等的结点。（因为如果相同时，插入失败 ）

 

 

 

分叉关系：

 

 

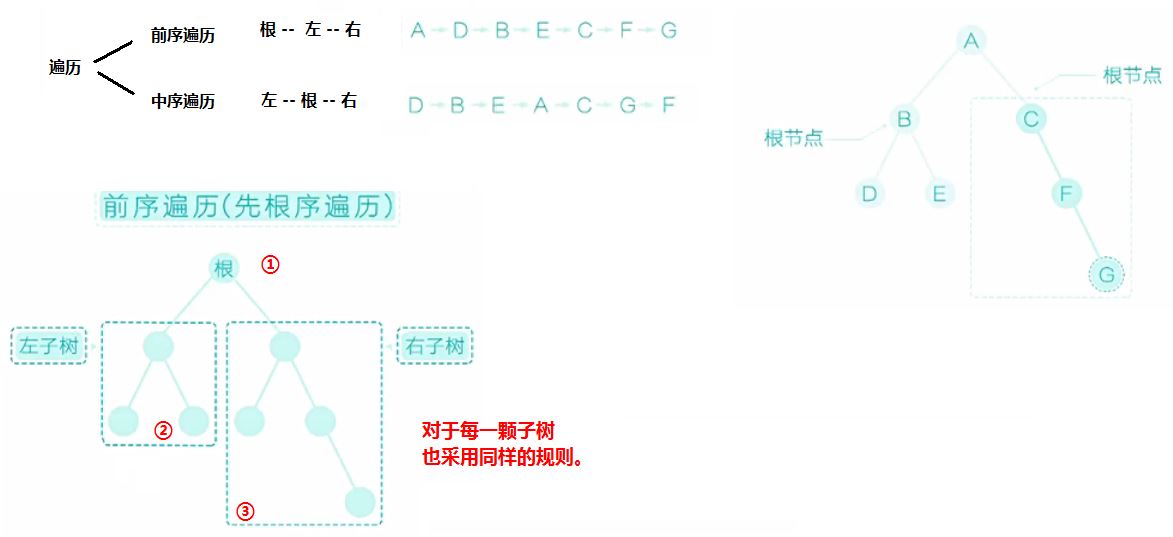
--对二叉树的遍历操作：

 

 

 

 

 

******************以下是测试二叉树的中序遍历 和 前序遍历的java代码*****************************************************

 代码如下：

package test;
/**测试二叉排序树*/
class BiTree{
    private int data;
    private BiTree left;    // 指向左子树的指针
    private BiTree right;   // 指向右子树的指针
    //有参构造方法
    public BiTree(int x){
        data = x;
    }
    
    public void add(BiTree x){
        if(x.data < this.data){
            if(left == null){
                left =x;
            }else{
                left.add(x); //递归处理
            }
        }else{
            if(right == null){
                right= x;
            }else{
                right.add(x); //递归处理
            }
        }
    }
    
    //中序遍历
    public void travel(){
        
        if(left != null){
        left.travel();
        }
        
        System.out.println(data);
        
        if(right != null){
            right.travel();
        }

    }
    //前序遍历
    public void travel2(){
        
        System.out.println(data);
        
        if(left != null){
        left.travel2();
        }
        
        if(right != null){
            right.travel2();
        }

    }
}

public class TestTree {
    public static void main(String[] args) {
        BiTree t = new BiTree(12);
        t.add(new BiTree(9));
        t.add(new BiTree(5));
        t.add(new BiTree(8));
        t.add(new BiTree(11));
        t.add(new BiTree(20));
        //中序遍历
        System.out.println("中序遍历如下：");
        t.travel();
        //前序遍历
        System.out.println("前序遍历如下：");
        t.travel2();

    }
}

 

 

********************************二叉树中序遍历和前序遍历测试完毕*******************************************************

测试结果如下：

 

 

 

 

 

 

视频链接： http://baidu.iqiyi.com/watch/7780896892997631108.html?page=videoMultiNeed

 

 

参考文档： https://blog.csdn.net/xiaoquantouer/article/details/65631708