散列表(哈希)
散列表 ( 哈希 )
简介
我们来讲述散列表。
散列表是一种数据结构,它具有以下性质:
- 应用广泛
- 查找快速
- 等
举个例子。
你在超市工作,一位顾客来购买商品,你家超市刚刚好没有自动销售机,你得亲自去查找该商品的价格。如果我们是这样的话,那么顾客每买一个商品,都要找一下该商品并且知道它的价格。那么我们非常花费时间。如果我们能够找到这样一个人:能够记住所有商品的价格的人。那么我们在帮顾客结账的时候将会非常快速。
即使你是用一个小本本把你商店的东西都记上了,并且是按照一定的顺序记号的。即使使用二分查找,那么我们也会花费一定的时间。想必此时顾客已经不耐烦了。他们可能会说:“怎么这么久!!!”,然后你的商店可能会产生很多很多的怨气......

我们从数据结构的方面去看这个问题,那么所有的商品就有了这样的一个特性:商品的key 以及 商品的卫星数据 。
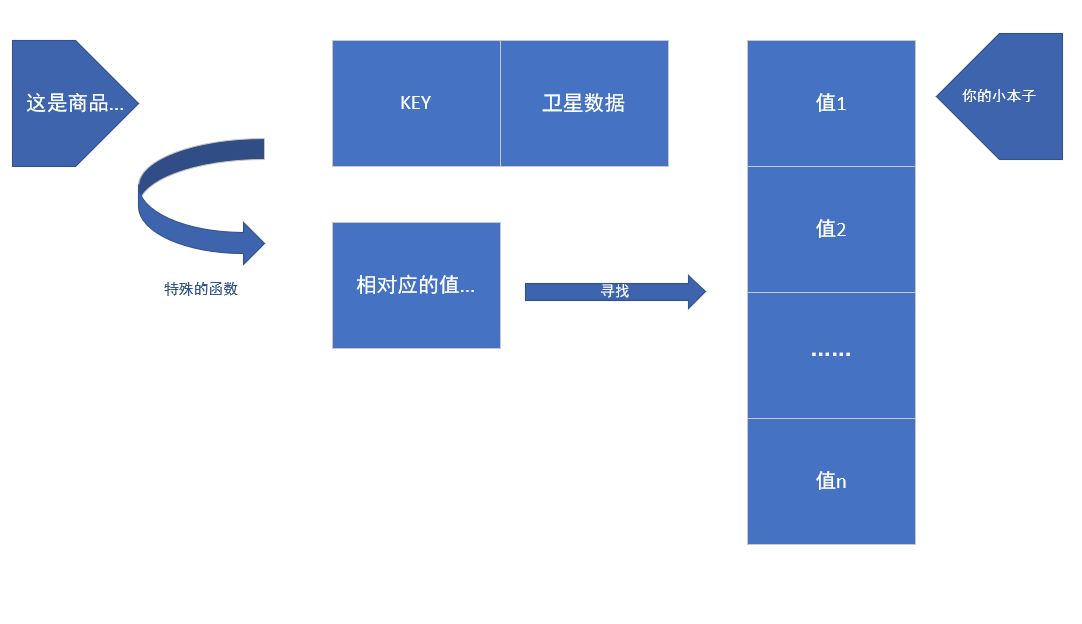
如果我们按照一个特殊的函数去把相对应的 KEY 值转换成另一个东西,并且记录在小本子上,我们只需直接翻到这个本子相对应的部分,就可以找到了该商品的价格了,以及还有其他的信息。
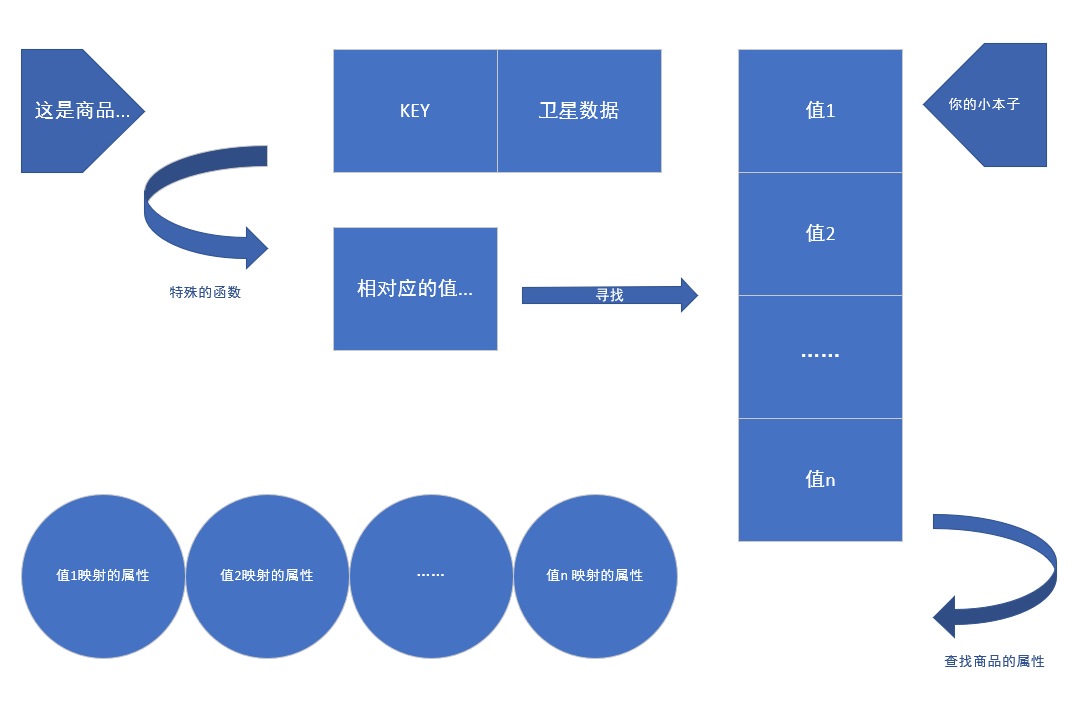
散列函数
那么我们的问题来了,我们该怎样创建这个数据类型呢?首先了解一下,散列函数
散列函数是“将输入映射到数字”
散列函数可能是没什么规律的,但是也必须得满足一定的要求:
- 必须是一致的,也就是每一个值都有它的唯一确定的一个值与它对应
- 它应该将不同的输入映射到不同的数字中。
- 应该还是离散型分布的,分布越离散,越有助于我们以后的运算
如果不是离散性的话,那么我们就可能会导致冲突现象特别明显。就比如我们有一个函数是这样的 y=x 2 ,那么我们输入-1,+1的时候,他们的值是一样的,此时产生了冲突性.......
散列函数总能够精确地指出我们在小本本写的东西的地址,或者说是第几页、第几条。这样的话,你就基本不用查找了,通过一个函数,直接就能够把这个地址找到了,然后你就可以很快地给别人结账......
主要有以下的原因:
- 散列函数总是将同样的输入映射到相同的地址上。
也就是说,我每一次调用这个散列函数的时候,它每一次都能给我相同的一个值,并且不会改变。这就说明,当你需要找到一样商品的时候,请你输入商品的 KEY 值,那么其对应的卫星数据就会很容易地被你在小本本上找到
- 散列函数将不同的输入映射到不同的地址中。
这个也是说,当我们找了商品1,还想找商品2的时候,输入其key值,我们所得到的值也是不一样的。这样就能保证每一个商品都有一个所对应的地址,从而我们能够很好地知道该商品在我们小本本上的页数
- 散列函数是有一个上界的,这个上界就是我们小本本的最大页码。它只能返回我们小本本的最大页码,如果超过了,那这就是一个无效的散列函数。
就好比如,我们的小本本有50页,那么我们的散列函数如果被输入一个数据之后返回51,那么我们改写到我们小本本的哪个地方呢?对吧。
一个好的散列函数需要有什么特点?
- 满足简单均匀散列假设
散列假设 : 每个关键子都被等可能地散列到 m 个槽位中的任何一个,并与其他关键字已散列到哪个槽位无关
- 好的方法导出的散列值,在某种程度上应独立于数据可能存在的任何模式
我们常用的构造散列函数有以下几种常用的方法
- 数字分析法
如果事先知道关键字集合,且每个关键字的位数比散列表的地址码位数多,每个关键字由n位数组成,如果k1k2...kn ,则可以从关键字中提取数字分布比较均匀的若干位作为散列地址
- 平方取中法
- 如果取关键字平方后的中间几位或其组合作为散列地址,则使随机分布的关键字得到的散列地址也是随机的,具体所取的位数由表长决定。
- 实用情况 : 不能事先了解关键字的所有情况,或难于直接从关键字中找到取值较分散的几位
- 折叠法
将关键字分割成位数相同的几部分,然后取这几部分的叠加和作为散列地址称为折叠法
- 除留余数法
假设散列表表长为 m ,选择一个不大于 m 的数 p ,用 p 去除关键字,除后所得余数为散列地址 也就是 H( key ) = key % p ,p 可以选取小于表长的最大质数
冲突
- 定义:两个关键字可能映射到同一个槽中。我们就称这种情形为冲突
为了解决这种方法,我们可以有以下的一些思想:
- 为了解决冲突,我们精心设计一个 散列函数
- 可以使用开放地址法
- 可以使用链接法
通过实验,我们更能够发现,仅仅是通过设计散列函数来解决冲突是远远不够的,好比如,一个散列函数 h 必须是一个确定的,因为某一个给定的输入 k 应始终产生相同的结果 h(k)。 但是由于| U | > m,所以至少有两个关键字,其散列值是相同的。(U是全域,m是散列表大小)
几种不同方法处理冲突时散列表的平均查找长度
影响平均查找长度的因素只有两个------处理冲突的方法和装填因子α
| 冲突的处理方法 | 查找失败长度 | 查找成功长度 |
|---|---|---|
| 线性探测法 | 1/2 * (1+1/(1-α)) | 1/2 * (1+1/(1-α)2) |
| 二次探测法/伪随机探测法 | -1/α * ln(1-α) | 1/(1-α) |
| 链地址法 | 1+α/2 | α+e-α |
开放地址法
开放地址法的思想是: 把记录都存储在散列表数组中,当某一记录u关键字 key 的初始d散列地址H0=H(key)发生冲突时,以H0为基础,采取合适的方法得到另一个地址H1,如果H1仍然发生s冲突,再以H1为基础球下一个地址H2。如果H2仍然从图,那么继续寻找H3,H4,H5....一直找到不冲突为止,那么Hk为该纪录在表中的散列地址。
- 线性探测法
如图所示,我们已经有了一些值在其中,然后我们要插入一个值,那么根据函数,我们求出了值,然后放入其中......

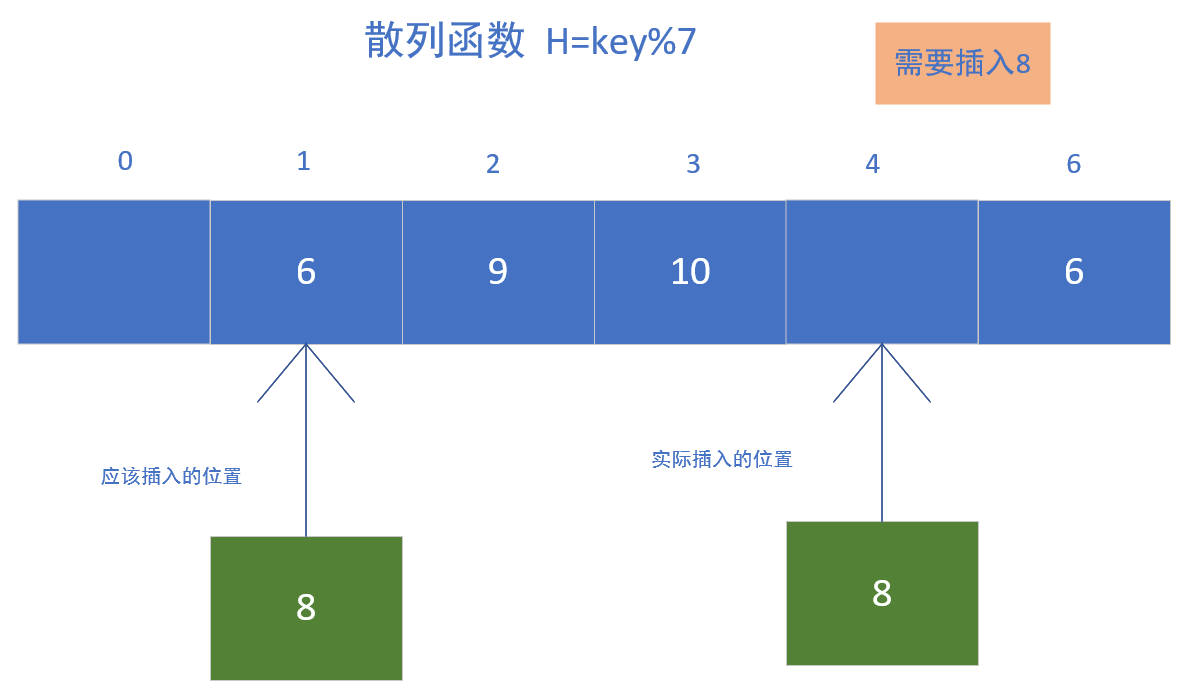
这样子,我们算是解决了冲突问题。这种探测法可以称为线性探测法,可以把散列表假想成一个循环的表,当发生冲突时,从冲突地址开始往后寻找空余的空位,然后插入。
- 二次探测法
二次探测法它的形式类似于平方,它是从+1,-1的平方开始,一直到找到对应的位置。
偏移量 di=(1)2,(-1)2,(2)2,(-2)2,(3)2,(-3)2......,(k)2,(-k)2, ( k<=m/2 )
- 伪随机探测法
这种方法就是使用伪随机数,得到随机数列,那么偏移量di=伪随机数序列
在线性探查中,比较容易出现一次群集和二次群集的现象,所以仍然不是很好地算法(自我认为),并且,使用开放地址法的散列表中,如果需要删除某些元素,那么会显示得比较困难或者说麻烦。
- 假设这个元素没有偏移,那么就可以直接通过散列函数定位到该地址,然后删除
- 如果又偏移,那么我们需要通过计算偏移量来找到该元素,然后删除这个值
一般,我们还是采用链接法来解决冲突。
链接法(也称链地址法)
链接法思想是: 把具有相同散列地址的记录放在同一个单链表中,称为同义词链表
方法是,在一个数组指针中,放置各个链表的头指针,凡是散列地址为i的记录都以重复的方式插入到该数组指针中。
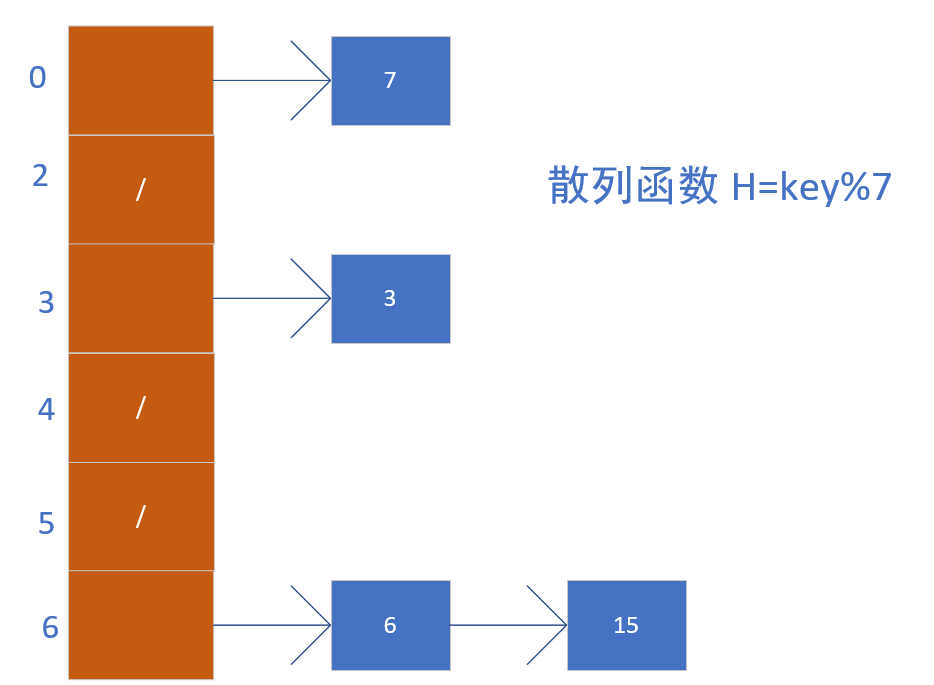
如果散列表中的链表是双向连接的,那么删除一个结点的时间复杂度就可以在O(1)的时间内完成。如果散列函数分布不均匀,使用链接法很容易造成只建立一个链表的形式或者两个链表的形式,那么这个时候便扩大了时间
链接法对比与开放地址法的优缺点
- 拉链法的处理冲突简单,并且没有堆积现象
- 拉链法是动态申请空间的,更适用于做表之前无法确定表长的情况
- 删除结点操作简单,并且速度快
| 比较项目 | 开放地址法 | 链地址法 |
|---|---|---|
| 空间 | 无指针域,存储效率高 | 附加指针域,存储效率较低 |
| 查找 | 有一次二次聚集现象,查找效率较低 | 无一次二次聚集现象,查找效率高 |
| 插入删除 | 不容易实现 | 比较容易实现 |
| 适用情况 | 表的大小固定,适用于表长无变化的情况 | 结点动态生成,适用于表长经常变化的情况 |
名词解释
-
KEY:商品的key有很多种,比如一个商品有它的名字,商品价格等等,那么我们待会可能需要用到这些东西,所以我把它叫成了KEY
-
商品的卫星数据:所谓的卫星数据呢,就是除了 KEY 以外的其他数据。比如,我们把商品的名字作为了 KEY 之后,那么其他的数据就被称作了卫星数据了。形象地解释就是, KEY 是一个行星,其他的数据就像是卫星一样围着 KEY 转动,就像是卫星一样(这是《算法导论》排序里面的一个名词,我拿来使用了)
-
群集: 多个数据同时集中在一个地方,然后我们得向下探查
-
一次群集: 初始探查位置决定了整一个序列,m种探查序列,然后因为是通过一次函数,所以容易发生群集线性
-
二次群集: 如果两个关键字的初始探查位置相同,那么它们的探查序列也是相同的,但是由于h(k1,0)=h(k2,0)蕴含着h(k1,i)=h(k2,i)这种性质会导致轻度的群集
-
装填因子α:散列表的装填因子α定义为:α=(表中填入的记录数)/(散列表的长度)
α标指散列表的装满程度,α越小,发生的冲突可能性就越小,α越大,表中填入的记录个数越多,那么发生的冲突的可能性就越大。
借鉴《算法导论》,《算法图解(图灵程序设计丛书)》,《数据结构(C语言版)》


